Total Internal Reflection - TIR

Dive into the Dazzling World of Total Internal Reflection (TIR)!
Have you ever wondered why diamonds sparkle so brilliantly or why you see water a few meters ahead on the highway on a hot summer day while driving? The answer lies in a fascinating phenomenon called Total Internal Reflection (TIR). In this interactive A-Level Physics tutorial, we'll unlock the secrets of TIR and its mind-bending effects on light!

Get ready to:
Master the principles of TIR through clear explanations and engaging animations. Explore real-world applications of TIR, from the dazzling sparkle of diamonds to the magic of fiber optics that power the internet!

Test your understanding with quizzes and activities.

By the end of this tutorial, you'll be able to:

Are you ready to embark on this journey of light and discovery? Let's begin!

 

 

Critical Angle - C

When light goes from a denser medium to a less dense medium, at a certain angle of incidence, the refracted ray goes along the boundary between the two media. The incident angle on this occasion is called the critical angle for the substances.

 

 

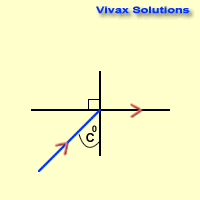
n_g = sin 90 / sin c
sin c = 1/ n_g
c = sin^-11/ n_g
c = sin^-1(1 /n_g)

 

Media	Critical Angle
glass / air	420
water / air	480
glass / water	630

 

You can find the critical angles for various substances by the following programme:

 

Total Internal Reflection

 

When light goes from a denser medium to a less dense medium, as the angle of incidence exceeds the critical angle, the ray reflects back to the denser medium. This phenomenon is called Total Internal Reflection.

Total Internal Reflection is a very efficient reflection, as the loss of light energy is almost negligible.

 

Total Internal Reflection - interactive practice

You can animate the following applet: the angle of incident will change and the angle of reflection will change in proportion to it. You will see the critical angle and total internal reflection too.

 

Uses and Effects of Total Internal Reflection

 

1. Reflecting prisms
   
   

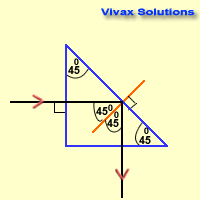
2. In optical instruments, right-angled prisms are widely used to divert the course of light rays. As the total internal reflection takes place within them, the loss of light energy can be kept to a minimum. So, the prisms are preferred to mirrors for the purpose of reflection.
3. Mirage
   
   
   
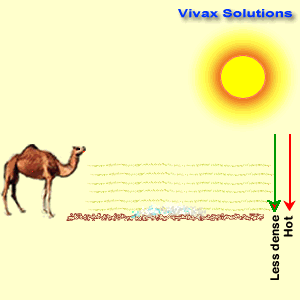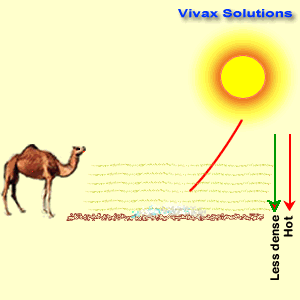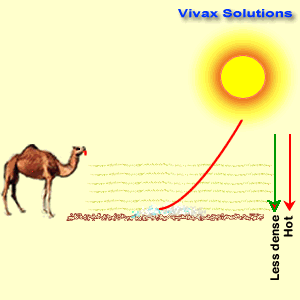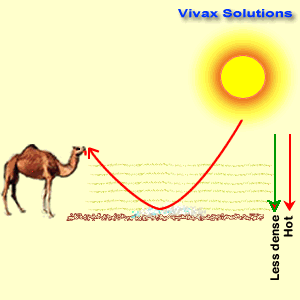
4. On hot summer days or in the deserts, patches of water appear to us, some miles in front of us, only to find none when we approach them. This phenomenon is caused by the total internal reflection. The air layers on the ground become hot and less dense in these places and light, when comes down has to pass through these less-dense layers. At a certain point, the light exceeds the critical angles and the total internal reflection takes place on a vast scale, creating the illusive puddles of water.


5. Sparkles in diamonds
   
   
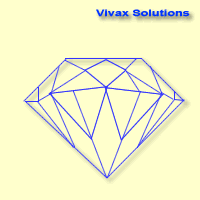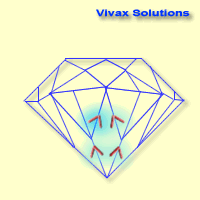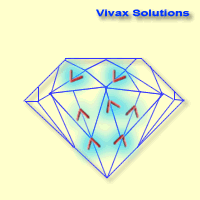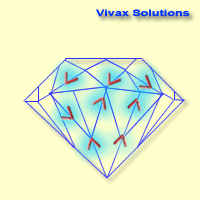
6. The sparkles inside diamonds are cause by total internal reflection. Diamond is well-known for its toughness - very dense and μ is very high; larger refractive index means smaller critical angle. Therefore, when light enters a diamond, the possibility of it being subjected to total internal reflection is very high, that in turn causes sparkles.
7. Optic fibres
   
   
   
8. Optic fibres revolutionized the communication that we take for granted today. This humble device - a thin flexible glass fibre with a coating - carries light through a distance of miles and miles, with a very little loss of its energy, thanks to total internal reflection. The trick is done by keeping the outer layer known as cladding less dense relative to the inner dense core - the first condition for total internal reflection. Since light enters almost parallel to the fibre, the angle of incidence is high and it easily exceeds the critical angle that triggers off the total internal reflection. The flexibility of the fibres, light weight, low cost and the ability to send light signals through them with very little loss of light, make then indispensable in modern communication networks.
9. Medical uses - the endoscope
   
   
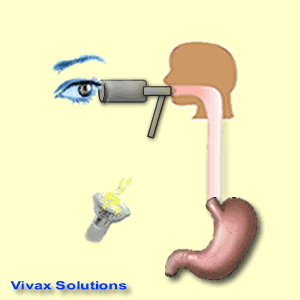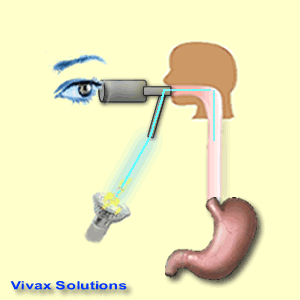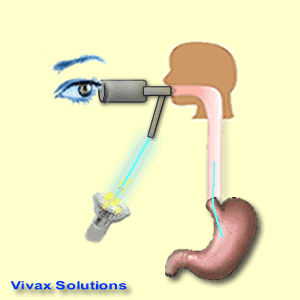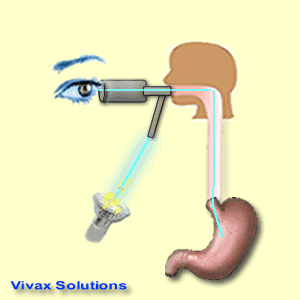
10. This is an instrument consisting of optic fibres. It is used by the medical professionals to see inside the body. The flexibility of optic fibres contributed to the invention of this device.

 

 

Worked Examples on TIR

E.g.1

A ray of light travels from a certain medium with a refractive index of 1.5 to another medium with a refractive index of 1.2. At what minimum angle of incidence will the light undergo total internal reflection?
We can use the formula for critical angle: sin(c) = n2 / n1, where n2 is the refractive index of the rarer medium and n1 is the refractive index of the denser medium.
sin(c) = 1.2 / 1.5 = 0.8.→ c ≈ 56.4°.
If the angle of incidence exceeds 56.4°, the ray will reflect back into the denser medium.

E.g.2

A light pipe is made of glass with a refractive index of 1.5. If a ray of light enters the pipe at an angle of incidence of 40° with respect to the normal. Will it undergo total internal reflection?
Since the critical angle for glass-air interface is typically around 42 degrees - use the above calculator - and the angle of incidence here is 40°, the light will not undergo total internal reflection. It will refract out of the glass pipe into the air without being subjected to TIR.

E.g.3

Application Challenge:
Design a simple experiment to demonstrate TIR using everyday materials.
Solution:
You can fill a glass with water and shine a laser pointer at the water surface from different angles, from the water. When the angle of incidence is less than the critical angle, around 42°, the laser beam will refract into the water. However, as you increase the angle, you will observe a point where the laser beam completely reflects back into the water, demonstrating TIR.You need to take extra care by not exposing your eyes directly into the laser beam, though.

E.g.4

ABC is a right-angled prism with AC being the longest side. A light ray enters through AC at right angles and hits AB, reflects and then goes out through BC. Show this prism can never be an isosceles prism.

 

 

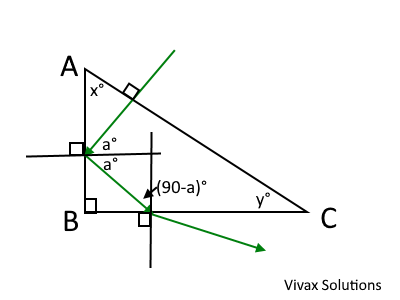
Using simple geometry,
a = 90 - (90 - x) = x
Since TIR takes place at the surface, AB, x > c, where c is the critical angle.
x > c → 1) At the surface, BC, TIR does not take place. Therefore, 90-a < c
Since a = x, 90 - x < c → 2)
For the right-angled triangle, 90 - x = y
From 2), y < x
Combining 1)and 2),
x > c > y
x° > y°
Therefore, the prism can never be an isosceles prism.

E.g.5

 

 

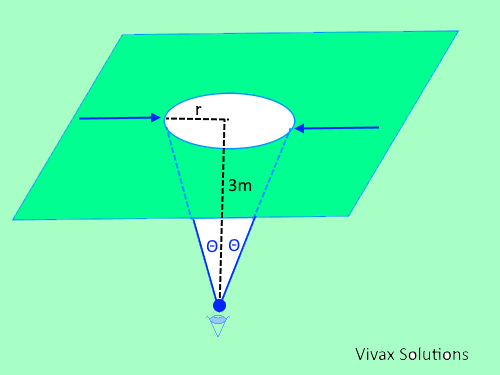
A diver sees a circular patch on the surface of a swimming pool, when looking up from a point at a depth 3m. Find the radius of the patch, if the refractive index of water is 4/3.
This happens when light that comes along the surface of the water refracts into the water, with the angle of incidence being the critical angle for water/air media.
sin Θ = 1/n → Θ = sin^-1(3/4) = 48°
tan 48 = r/3
r = 3.3m.

 

Please answer the following questions.

1. An isosceles right-angled glass prism can be used for the total internal reflection, but not a similar one made of ice. Explain.Take n_g = 1.5 and Take n_w = 1.3
2. Optic fibres are used as bundles of thin fibres instead of a thick single one. Explain this.
3. A light ray has to be diverted by 180⁰ inside a right-angled prism. Show how this is achievable, using a ray diagram.
4. Using a ray diagram show how two prisms are used to divert a ray of light inside a pair of binoculars while keeping the image the same way up.
5. ABC is a triangular prism with the angle between AB and BC being 60°. On the surface, there is a layer of a liquid and the side BC is in contact with a mirror. When a ray of light enters the prism between the two media along the side AB, it refracts and hits the side BC, before returning along the same path. Find the refractive index of the liquid.
   Answer: 1.15

 

Now that you have read this tutorial, you will find the following tutorials very helpful too: