Projectiles

In this tutorial, you will learn the following:

Projectile

An object that moves under gravity in the air is a projectile.

E.g.

• › A cricket ball that moves through the air, after being struck by a bat
• › A baseball that moves through the air, after being struck by a baseball bat
• › A football that moves in the air after being kicked
• › A dart that moves through the air
• › An arrow that moves through the air, having been fired by an archer

Suppose an object is projected at an angle of t to the horizontal at the speed of v. Since it moves both vertically and horizontally, the initial velocity has components both vertically and horizontally: the vertical component takes it up and the horizontal component takes it horizontally. The following image illustrates it:

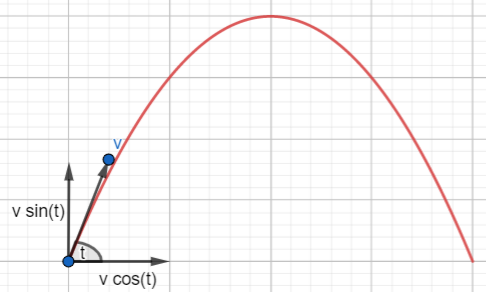
Since there is no horizontal force at work in the absence of air resistance, according to F = ma, the acceleration is zero. So, the horizontal velocity remains constant throughout the motion. The vertical velocity, however, goes down, as the gravitational pull acts in the opposite direction - downwards. When the projectile reaches the peak, it becomes zero and then changes the direction and increases as it goes down.

You can practise the changes in velocity of a projectile interactively with the following applet; just move the slider - time - and see the changes:

 

Maximum Height
This is he maximum vertical height reached by the projectile.

Time of flight
This is the time during which the object has been in the air.

Maximum Horizontal Range
This is he maximum horizontal distance travelled by the projectile.

The following worked examples cover the above in detail.

Projectiles - Problem Solving

Throughout these examples, the acceleration due to gravity, g, is assumed to be 10ms^-2 to make calculations smooth.

E.g.1

A ball is projected at 20√2 m/s, at an angle of 45⁰ to the horizontal. Find the following, by assuming that g = 10ms^-2:

1. The maximum height
2. The time of flight
3. The maximum horizontal range

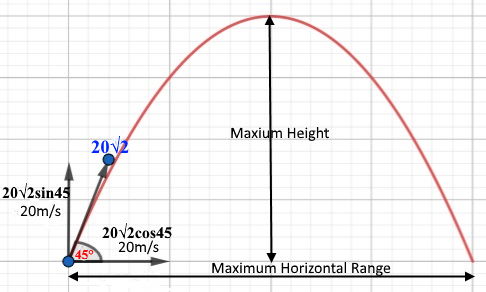
1. For vertical Motion, until the objects comes to an instant halt
   ↑ v² = u² + 2as
   u = v sin(45) = 20√2 &1/√2 = 20; a = -10; s = h
   0 = 400 - 2x10xs
   h = 20 m.
2. When the object reaches the highest point,
   ↑ v = u + at
   u = v sin(45) = 20√2 &1/√2 = 20; a = -10; v = 0
   0 = 20 - 10t
   t = 2 s
   The time of flight = 2x2 = 4 s.
3. → s = ut + 1/2 at² u = 20√2 cos(45) = 20 x 1/√2 = 20; a = 0; t = 4
   s = 20x4 + 0
   s = 80 m.

E.g.2

A ball is projected at 20 m/s, horizontally from a tower of height 20 m. Find the following, by assuming that g = 10ms^-2:

1. The time of flight
2. The maximum horizontal range
3. The velocity after 1 second
4. The velocity at which it hits the ground

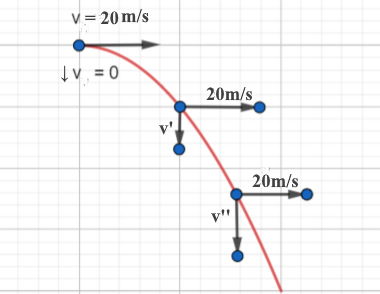
Since it was projected horizontally, there would be no vertical speed at the beginning.

1. For vertical Motion, until it hits the ground,
   ↓ s = ut + 1/2 at²
   u = 0; a = 10; s = 20
   20 = 0 + 5t²
   t² = 4 => t = ±2
   t = 2s.
2. When the object reaches the ground,
   → s = ut + 1/2 at²
   u = 20; a = 0; t = 2
   s = 20x2 + 0
   s = 40 m
   
3. After 1s, it stats moving downward; it has a vertical velocity and a horizontal velocity, which is constant.
   ↓ v = u + at
   u = 0; a = 10; t = 1
   v = 0 + 1x10
   v = 10 ms^-1.
   → v = u + at
   u = 20; a = 0; t = 1
   v = 20 + 0
   v = 20 ms^-1.
   So, the resultant velocity = √(10² + 20²)
   ↘ v = √500 = 10√5 m/s.
4. When it hits the ground too, it has a vertical velocity and a horizontal velocity, which is constant.
   ↓ v = u + at
   u = 0; a = 10; t = 2
   v = 0 + 2x10
   v = 20ms^-1.
   → v = u + at
   u = 20; a = 0; t = 2
   v = 20 + 0
   v = 20 ms^-1.
   So, the resultant velocity = √(20² + 20²)
   ↘ v = √800 = 20√2 m/s.

 

E.g.3

A ball is projected at 20√2, at an angle of 45⁰ to the horizontal, from the top of a tower of height 60m, upwards. Find the following, by assuming that g = 10ms^-2:

1. The time of flight
2. The maximum horizontal range
3. The maximum height reached by the object
4. The velocity at which it hits the ground

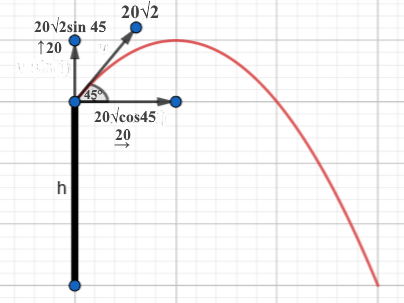
When the object reaches the level of the top of the tower again, its displacement is zero; below that level, it is negative.

1. For vertical Motion, until it reaches the ground,
   ↑ s = ut + 1/2 at²
   u = 20√2 sin(45) = 20; a = -10; s = -60
   -60 = 20t - 5t²
   5t² - 20t - 60 = 0 => t² -4t - 12 = 0 => t = 6 or t = -2
   t = 6s.
2. When the object reaches the ground,
   → s = ut + 1/2 at²
   u = 20√2 cos(45) = 20; a = 0; t = 6
   s = 20x6 + 0
   s = 120 m
   
3. ↑ v² = u² - 2as
   u = 20; a = -10; v = 0
   0 = 400 - 2x10xs
   s = 20 m
   Total height = 20 + 60 = 80 m.
4. ↓ v = u + at
   u = 20; a = -10; v = ? t = 6
   v = 20 - 10x6 = -40 m/s
   → since horizontal velocity remains the same, v = 20
   So, the resultant velocity = √(40² + 20²)
   ↘ v = √2000 = 20√5 m/s.

 

E.g.4

A ball is projected at 12 m/s at an angle, 20° to the horizontal from a tower of height 10m. Find the following, by assuming that g = 10 ms^-2:

1. The time of flight
2. The maximum horizontal range
3. The velocity at which it hits the ground

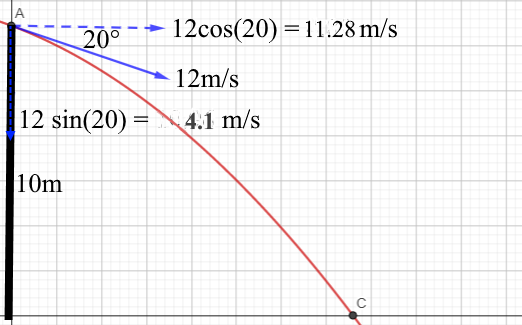
1. ↓ u = 4.1, s = 10, t = ?, a = 10
   s = ut + 1/2 at²
   10 = 4.1t + 1/2 x 10 x t²
   10 = 4.1t + 5t²
   5t² + 4.1t - 10 = 0
   t = 1.06s or t = -1.88s
   Time of flight = 1.06 s
2. → u = 11.28, a = 0, t = 1.06, s = ?
   s = ut + 1/2 at²
   s = 11.28 x 1.06
   s = 11.95 m
3. ↓ u = 4.1, a = 10, t = 1.06 v = ?
   v = 4.1 + 10 x 1.06
   v = 14.7 m/s
   → the horizontal velocity remains the same.
   ↘ v = √(14.7² + 11.27²)
   v = 18.52 m/s

E.g.5

A ball is projected at 5i + 20j from a tower of height 5 m Find the following, by assuming that g = 10 ms^-2:

1. The time of flight
2. The maximum height
3. The maximum horizontal range
4. The velocity at which it hits the ground
5. The angle of between the ball and the horizontal, when it hits the ground

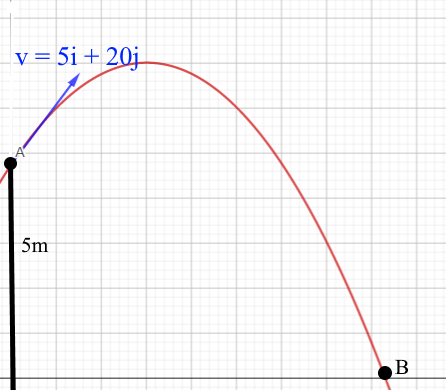
1. ↑ u = 20, s = -5 t = ?, a = -10
   s = ut + 1/2 at²
   -5= 20t - 1/2 x 10 x t²
   -5 = 20t - 5t²
   5t² - 20t - 5 = 0
   t = 4.2s or t = -0.2s
   Time of flight = 4.2 s
2. ↑ u = 20, a = -10, v = 0, s = ?
   v² = u² + 2as
   0 = 400 - 20s
   s = 20 m
   Maximum height = 5 + 20 = 25 m
3. → u = 5, a = 0, t = 4.2 s = ?
   s = 5 x 4.2
   s = 21 m
4. → Since there is no horizontal acceleration, the horizontal velocity remains the same - 5i
   ↑ u = 20, a = -10, s = -5, v = ?
   v² = u² + 2as
   v² = 400 + 2(-10)(-5)
   v² = 500
   v = 22.4 m/s
   ↘ v = √(22.4² + 5²)
   v = 22.9 m/s
5. ↘ tan θ = 22.4/5 = 4.48
   θ = 1.35°

Formulae of Projectile Motion

These are the main formulae involving the projectile motion. You, however, do not have to remember them! Just try to derive them using the SUVAT; it makes the learning process easier.

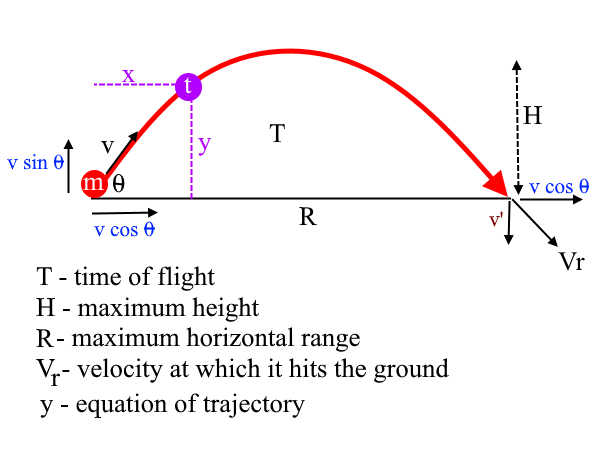
↑ u = vsinθ, v = 0, a=-g, s = H, t = T/2
v = u + at
0 = vsinθ + -gT/2
gT/2 = vsinθ
T = 2vsinθ/g
↑ u = vsinθ, v = 0, a=-g, s=H
v² = u² + 2as
0 = v²sin²θ - 2gH
2gH = v²sin²θ
H = v²sin²θ / 2g
→ u = vcosθ, a = 0, s = R, t = T = 2vsinθ/g
R = vcosθ(2vsinθ/g)
R = 2v²sinθcosθ / g
since sin2θ = 2sinθcosθ
v²sin2θ/g
↑u = vsinθ, a = -g, t = t, s = y
s = ut + 1/2 at²
y = vsinθt - 1/2 gt² ------1)
→ u = vcosθ, t = t, s = x
x = vtcosθ => t = x/vcosθ
Sub in 1),
y = x tanθ - 1/2 gx²/v²cos²θ
y = x tanθ - gx²sec²θ/2v²
Since sec²θ = 1 + tan²θ
y = x tanθ - gx²(1 + tan²θ)/2v²

 

Maximizing the Horizontal Range

Suppose an object is projected at an angle, t, to the horizontal at v.

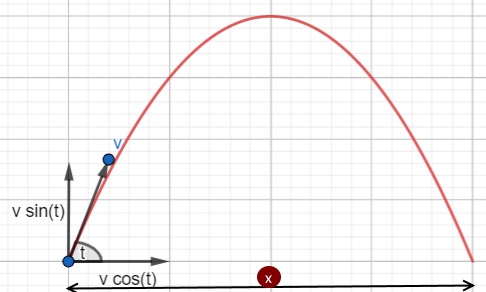
When it reaches the peak,
↑ u = v sin(t); v = 0; t = t
o = v sin(t) - at
t = v sin(t)/a
The time of flight= 2v sin(t)/a
→ s = x; u = v cos(t); a = 0; t = 2vsin(t)
x = 2v²sin(t)cos(t)
Since 2 sin(t) cos(t) = sin(2t) - a trigonometric identity
x = v²sin(2t)
dx/dt = 2v²cos(2t)
When x is maximum, dx/dt =0
2v²cos(2t) = 0
cos(2t) = 0
2t = 90⁰
t = 45⁰
So, the horizontal range is maximum when the angle of projection from the horizontal is 45⁰.
That means, if a cricketer or a footballer think of maximizing the horizontal range, here is the way!