Refraction of Light

When light goes from one substance to another, it changes both its speed and  path. This phenomenon is called Refraction.

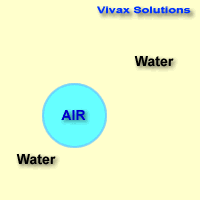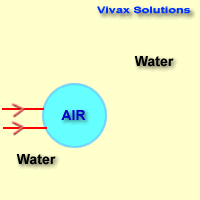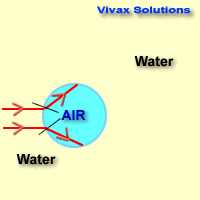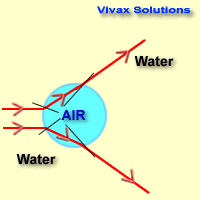
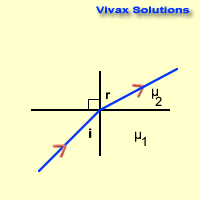
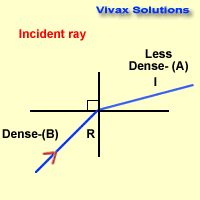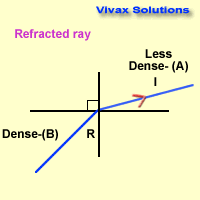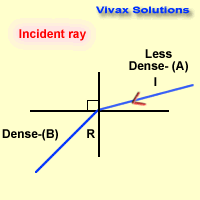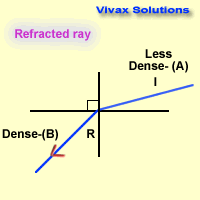i = angle of incidence
r = angle of refraction

As you can see, these angles can easily be used interchanging, depending on the direction of the light ray - from dense to less dense or vice versa.

The path taken by the light ray is the same regardless of its direction.
If light goes from less dense to dense - for example,  air to water - the refracted ray bends towards normal; on the other hand if it goes from dense to less dense - for example, glass to air - the refracted ray bends away from the normal.

The following animation sums up it all.

 

Laws of Refraction

1. The incident ray, refracted ray and the normal are in the same plane.
2. The ratio of sine value of incident angle and the refracted angle remains the same for two given substances. This is known as Snell's law.

This ratio is called the refractive index of the two given media.

If light goes from A to B,
AμB = sin i / sin r
AμB is called refractive index of B relative to A

If light goes from B to A,
BμA = sin r / sin i
BμA is called refractive index of A relative to B
You can see from the above formulae, that,

BμA = 1 / AμB

The refractive index of a medium relative to vacuum / air, is called its refractive index.
E.g.
aμg = μg refractive index of glass = 3 /2
aμw = μw refractive index of water = 4 /3

BμA = μA / μB

gμw = μw / μg = (4/3) / (3/2) = 8 / 9

E.g.1

AμB = 3 / 2, find BμA
BμA = 1 / AμB = 1/ (3/2) = 2 /3
BμA = 2 /3

E.g.2

A light ray strikes the boundary between air and glass at right angles. Show that it goes into glass without a change in direction.

 

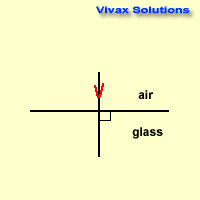
aμg = sin i / sin r
aμg = sin 0 / sin r = 0 / sin r
sin r = 0 => r = 0
So, the light ray goes without bending.

E.g.3

A light ray goes from glass to air with an angle of incidence 30⁰. Find the angle of refraction. μg = 3 / 2

 

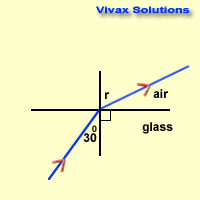
gμa = sin 30 / sin r = 0.5 / sin r
1/3/2 = 0.5/sin r
2/3 = 0.5/sin r
sin r = 0.75
r = 49⁰

E.g.4

A light ray goes from glass to air with an angle of incidence 42⁰ Find the angle of refraction and then comment on its path. μ = 3 / 2

 

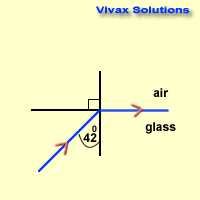
μg = 3/2 => aμg = 3 / 2
Since light goes from glass to air,
gμa = 1 / aμg = 2 / 3
2 / 3 = sin 42 / sin r
sin r = 1
r = 90⁰

E.g.5

A light ray goes from glass to air with an angle of incidence 60⁰ Show this ray will never refract. μg = 3 / 2

 

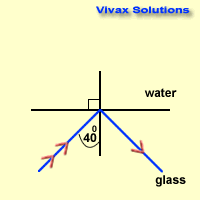
μg = 3/2 => aμg = 3 / 2
Since light goes from glass to air,
gμa = 1 / aμg = 2 / 3
2 / 3 = sin 60 / sin r = 0.8660 / sin r
sin r = 1.45
Since sin r > 1, this situation is impossible; so the light ray will not refract into air. Instead, it will refract back into glass.

A light ray enters water from glass with an angle of incidence of 40⁰ into water. Find the angle of refraction. μg = 3 /2, μw = 4 / 3

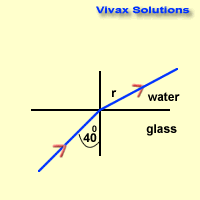
gμw = μw / μg = (4/3) / (3/2) = 8 / 9
8 / 9 = sin 40 / sin r
sin r = 0.7231
r = 46⁰

The Refraction Calculator

 

 

i	μ1	μ2

Please answer the following questions:

1. A light ray goes from air to glass, hitting the boundary at an angle of 40⁰. Find the angle of refraction.μg = 3/2
2. Explain with a ray diagram, as to why a pencil, when partially submerged in water, appears to be bent, to someone looking from a side.
3. Explain as to why the bottom of a swimming pool appears to be shallower than it really is, using a ray diagram.
4. An air bubble is trapped at the centre of a glass hemisphere. When you look at from outside, it does not appear to be refracted. Explain this.
5. A glass hemisphere is placed on a letter - the flat side - and looked at it from above. The letter appears to be where it really is. However, when you turned it upside down, the letters appear to be moving up. Explain this.
6. Show that a ray of light, while going through a glass block, emerges from it so that the incident ray is parallel to the emergent ray.
7. An air bubble is trapped in a glass sphere so that it is not at the centre, but on a horizontal diameter. Draw a ray diagram to show how it appears to someone when looking from outside through two opposite sides.
8. A swimmer looks at a bird flying over him in the air. Draw a ray diagram to show how it appears to him.