Logic Gates

 

Diodes

A device that can control the direction of the flow of a current is a diode; it is made of semiconductor materials such as silicon.

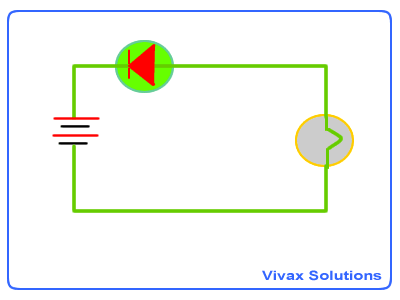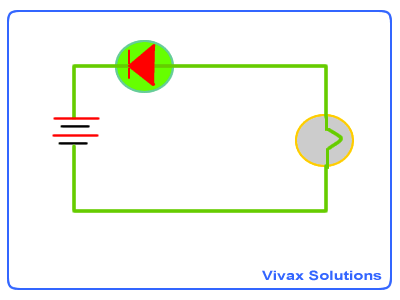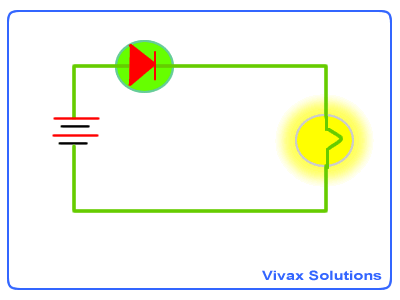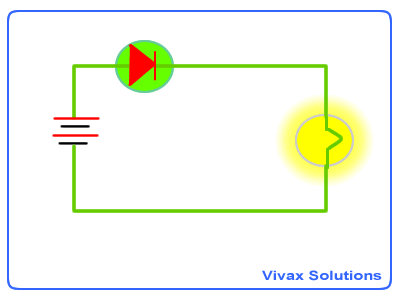
As you can see, the position of the diode can turn the current on or off.

That means, a diode can be used as a one way switch: if the wider end of it faces a positive terminal of a battery, it lets current through or else it cuts the current off.

Based on this system, a couple of switches are made and they are called logic gates. The input of these gates can be combinations of 'On' or 'Off' states and they are known as '1's or '0's. These are binary digits, that has been the basis of the Binary System. The output can also be '0's or '1's. That means, we can express the output of these systems in terms of '1' and '0' - binary digits.
In other words, the output of the logic gates can be used to interpret the numbers in binary form. This is the birth of computer systems; they recognize only '0' s and '1's.

The following animations show the major logic gates, their input's and output's.

 

 

Logic Gates

OR Gate

 

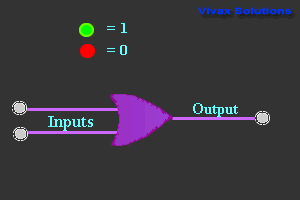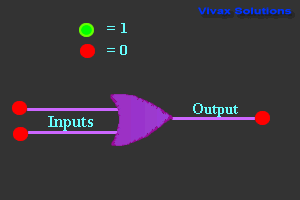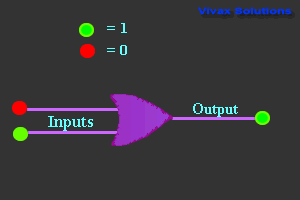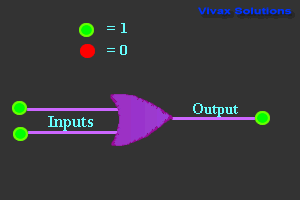
Truth Table
Left		Right
Top	Bottom	Output
0	0	0
0	1	1
1	0	1
1	1	1

AND Gate

 

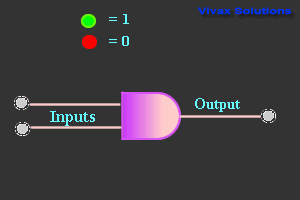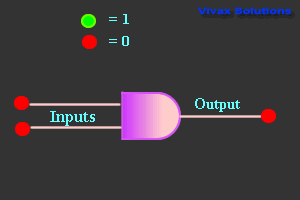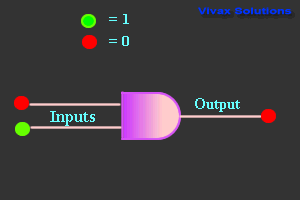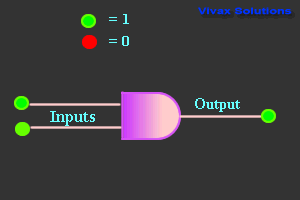
Truth Table
Left		Right
Top	Bottom	Output
0	0	0
0	1	0
1	0	0
1	1	1

NOT Gate

 

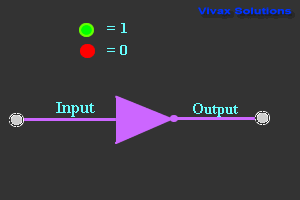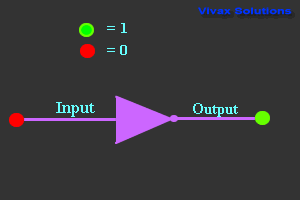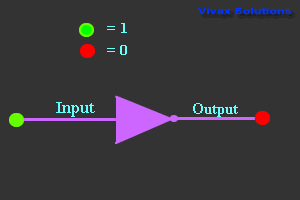
Truth Table
Input	Output
0	1
1	0

NOR Gate

 

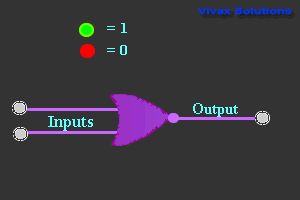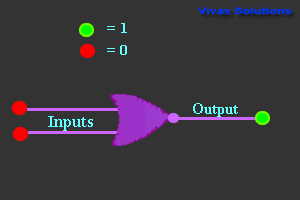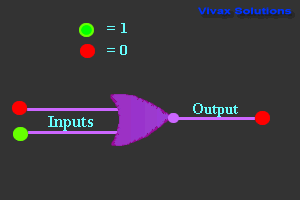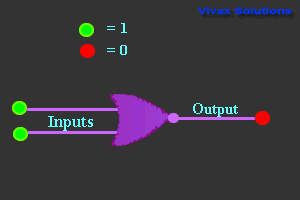
Truth Table
Left		Right
Top	Bottom	Output
0	0	1
0	1	0
1	0	0
1	1	0

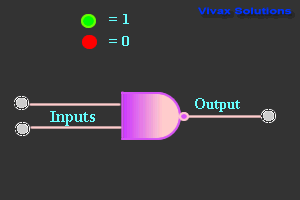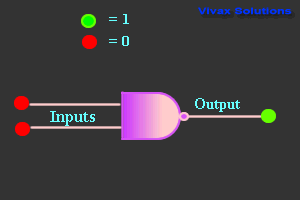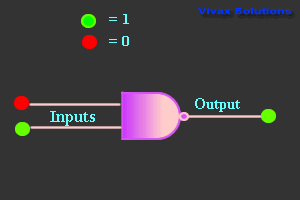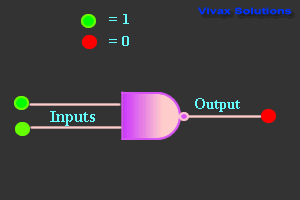
NAND Gate

 

Truth Table
Left		Right
Top	Bottom	Output
0	0	1
0	1	1
1	0	1
1	1	0

 

 

Practice Exercises

Construct a truth tables for each the following circuit of logic gates; then, check them with the corresponding animation that follows:

E.g.1

 

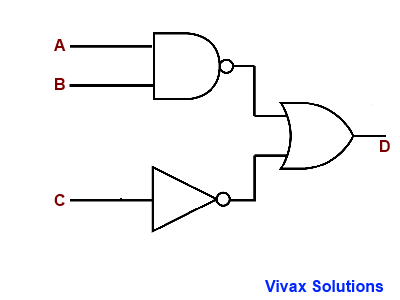
Since there are three inputs, the possibilities are, 2³ = 8. Here is the animated answer.

 

 

E.g.2

 

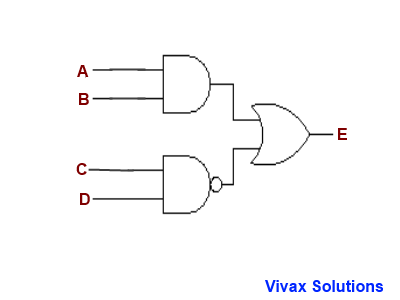
Since there are four inputs, the possibilities are, 2⁴ = 16. Here is the animated answer with some of the possibilities - not all.

 

 

E.g.3

 

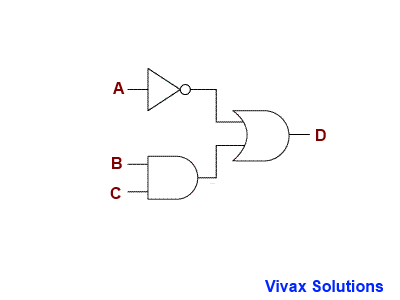
Since there are three inputs, the possibilities are, 2³ = 8, in this case too. Here is the animated answer with all the possibilities.

 

 

Uses of Logic Gates

Logic gates are used in almost every electronic device today that we take for granted; the following animation shows some of the role played by them in the things that we use everyday.

Washing Machine

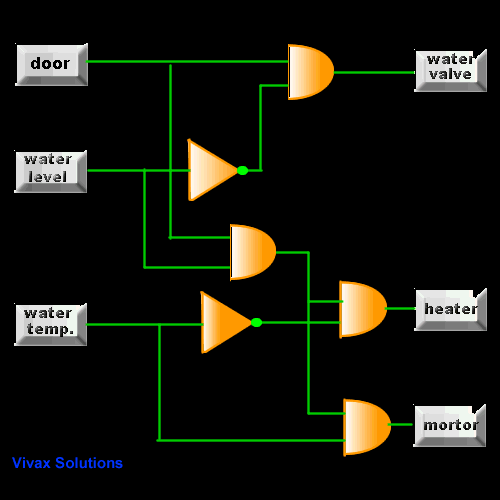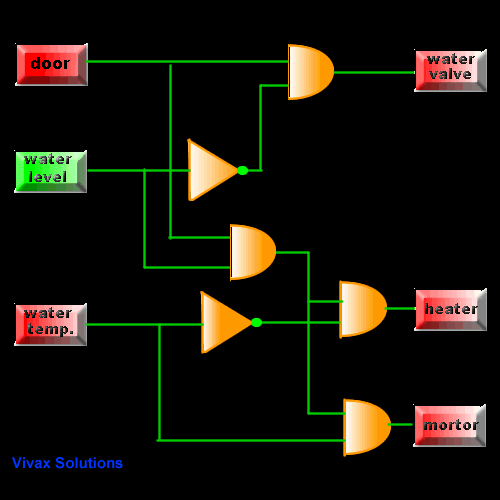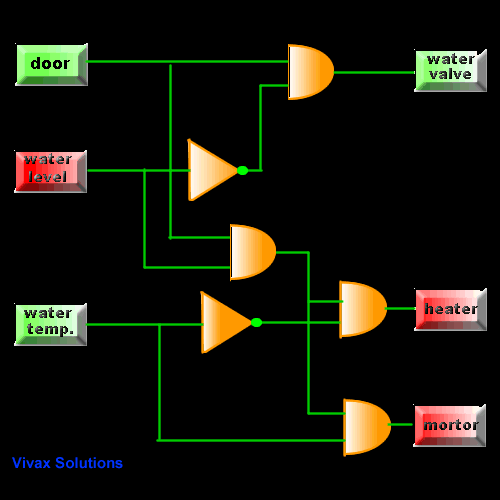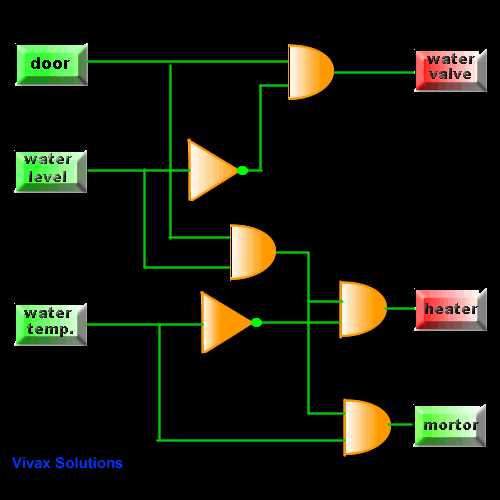
Have you noticed when the motor is turning on?  the right temperature, right water level and of course, the closure of the door - for obvious reasons.

7-digit Decoder

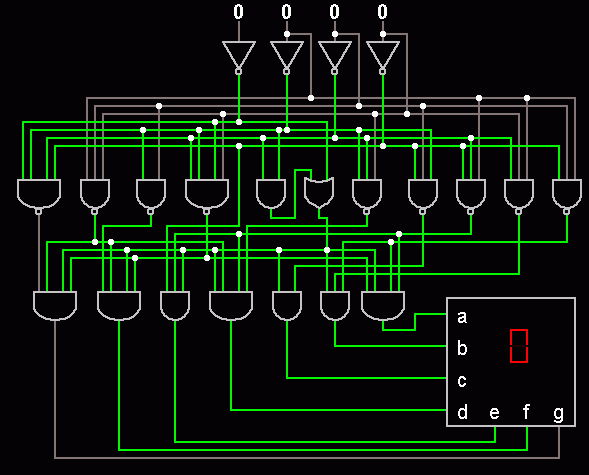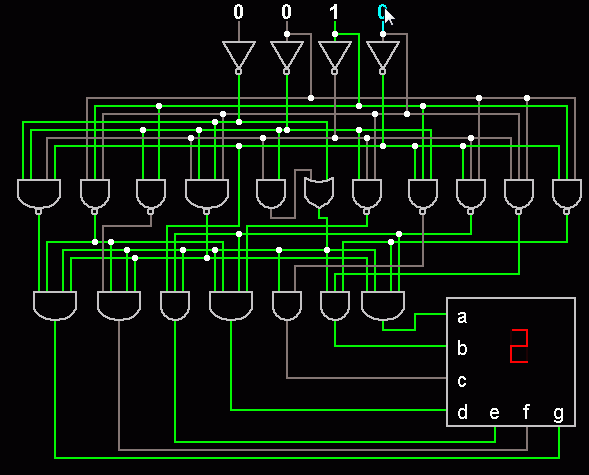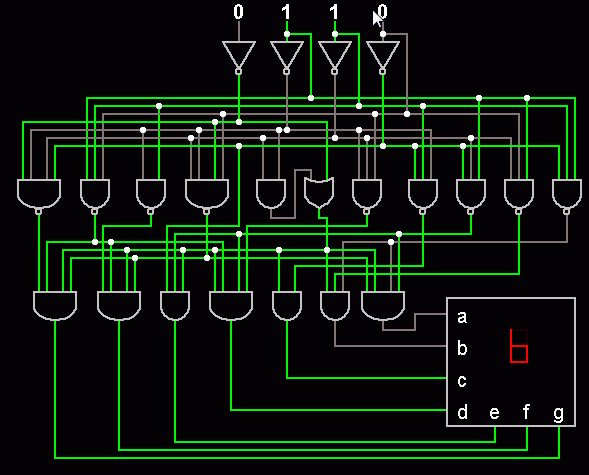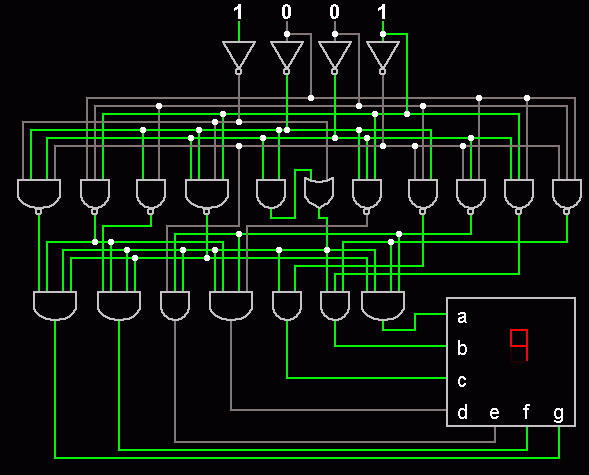
This is how a calculator displays the digits.

Do you want to practise what you learn? Here is a book for you: