Vernier Calliper
Master the Vernier Calliper with Our Interactive Simulator
Welcome to your ultimate guide to mastering the Vernier calliper! Whether you're a student, hobbyist, or professional, this interactive tutorial will equip you with the skills to take precise measurements with confidence.

Forget about textbooks and static images. Our innovative simulator brings the Vernier calliper to life, allowing you to practice and experiment in a virtual environment. Learn by doing as you manipulate the digital calliper, encountering various measurement scenarios.
From understanding the basic principles to tackling complex measurements, our step-by-step guidance and real-world examples will transform you into a measurement expert. Get ready to enhance your problem-solving abilities and achieve accurate results every time.
Let's dive in and unlock the potential of the Vernier calliper together! At the bottom of the tutorial, there will be an interactive quiz for you to gauge your knowledge on the instrument.
Vernier Calliper, in essence, is a simple device to measure very small lengths easily. The movable scale, also known as Vernier scale, is divided into 10 units. If it slides along the main scale, marked in mm, the gap between two the 0s between the two scales.
If the instrument is accurate, the two zeros must coincide.
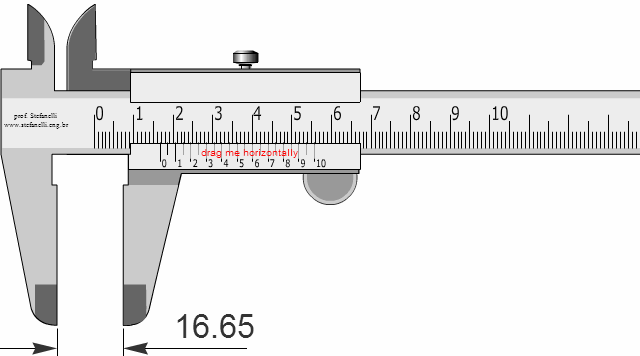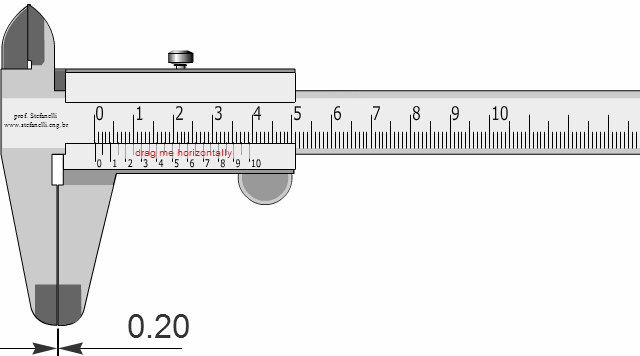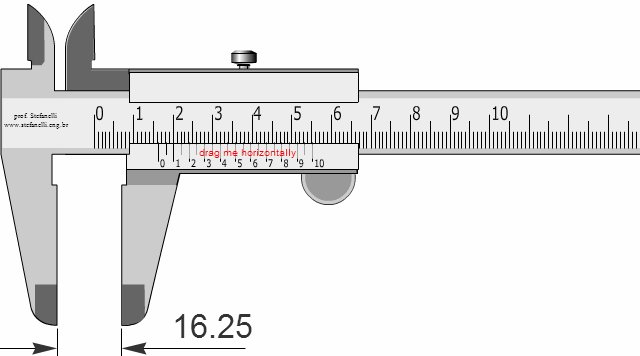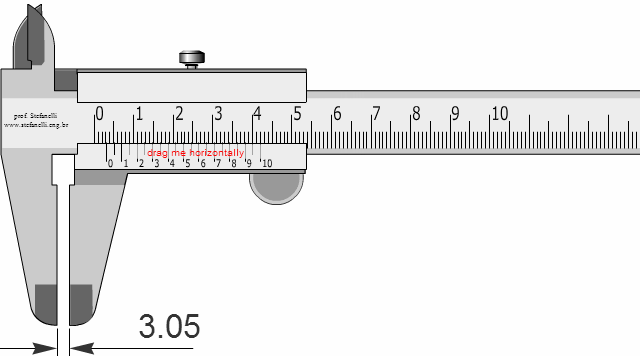
So,
10 Vernier units = 9 mm
1 Vernier unit = 9/10 mm
1 Vernier unit = 0.9 mm
The gap between 1 unit of the main scale and Vernier unit = 1-0.9 = 0.1 mm
With that, this particular calliper lets us measure lengths which are as small as 0.1 mm.
Therefore, the Vernier scale lets us measure us small lengths. The following animation describes the working of the device.
Please move the slider and study the reading.
Let's look at a few of the readings:
E.g.1
Suppose the three different lengths of the red string, read by the main scale, is 4 mm, correct to 1 mm. So its real length is greater than 4 mm and less than 5 mm. The correct value can be calculated as follows:
If 7 mm mark on the main scale coincide with 3th tick of Vernier scale
The value on the Vernier scale = 3x0.9 = 2.7 mm
Therefore, the gap between the two zeros of the scales = 7- 2.7 = 4.3
Length of the red wire = 4.3 mm
E.g.2
If 10 mm mark on the main scale coincide with 6th tick of Vernier scale
The value on the Vernier scale = 6x0.9 = 5.4 mm
Therefore, the gap between the two zeros of the scales = 10-5.4 = 4.6
Length of the red wire = 4.3 mm
E.g.3
If 12 mm mark on the main scale coincide with 8th tick of Vernier scale
The value on the Vernier scale = 8x0.9 = 7.2 mm
Therefore, the gap between the two zeros of the scales = 12-7.2 = 4.8
Length of the red wire = 4.8 mm
So, a certain pattern emerges between the real value and the Vernier reading that coincides with a tick of the main scale.
| Vernier Value | Real length |
| 3 | 4.3 |
| 6 | 4.6 |
| 8 | 4.8 |
.
.
.
| .
.
.
|
| n | 4+0.1n |
If the main scale reading is m and Vernier reading is n, then the real value = m + 0.1n
You can see that we can measure up to 0.1mm, thanks to the above Vernier Scale. Some Vernier Scales are, sometimes, divided into 20 or 30. The more divisions it has, the more accurate it becomes.
E.g.1
If 20 Vernier divisions coincide with 19 mm
20 Vernier units = 19 mm
1 Vernier unit = 19/20 mm
1 Vernier unit = 0.95 mm
The gap between 1 unit of the main scale and Vernier unit = 1-0.95 = 0.05 mm
With that, this particular calliper lets us measure lengths which are as small as 0.05 mm.
If the main scale reading is m and Vernier reading is n, then the real value = m + 0.05n
E.g.2
If 20 Vernier divisions coincide with 29 mm
30 Vernier units = 29 mm
1 Vernier unit = 29/30 mm
1 Vernier unit = 0.97 mm
The gap between 1 unit of the main scale and Vernier unit = 1-0.97 = 0.03 mm
With that, this particular calliper lets us measure lengths which are as small as 0.03 mm.
If the main scale reading is m and Vernier reading is n, then the real value = m + 0.03n
Are you interested in knowing how the animation was created> Please click here.
A Quiz on Vernier Calliper