The Kinetic Theory of Gases
Demystifying Gases: A Kinetic Theory Adventure!
Ever wondered why a balloon inflates when heated? Or how pressure cookers work? The answers lie in the fascinating world of the kinetic theory of gases! This A-Level physics tutorial will take you on a journey to understand gases on a microscopic level.
At the end of this tutorial, there is a fully interactive, Quiz, for you to gauge your understanding.
We'll delve into the basic assumptions of the theory, explore how tiny particles moving at high speeds explain the macroscopic behavior of gases, and see how this connects to the gas laws you've already encountered. Buckle up and get ready to unlock the secrets of gases!
The Kinetic Theory of Gases has put forward a series of assumptions in order to explain what has been observed experimentally in gases.
Although, their number may vary, the core message is the same. They are as follows:
- The molecules of a particular gas are identical and in random motion.
- The collisions between the molecules and the between them and the walls of the container are perfectly elastic.
- The volume of a molecule is negligible, compared with the volume of the container.
- There are no intermolecular attractions between the molecules.
- The time taken for a collision between two molecules is negligible compared with the time taken for the same between a molecule and the wall.
Based on these assumptions, a formula can be derived that connects the pressure, volume, the number of molecules, individual mass and of course, the mean velocity.
If an individual molecule collides with a wall, as shown in the animation, its momentum gets doubled.A gas molecule can move in any direction at a given time - in the x-direction, y-direction or z-direction.
Let's consider the motion in the x-direction, as shown in the animation; let the velocity be Ux
If the length of the cube, mass of the molecule and velocity are l, m and v respectively,
Momentum in the x-direction = mUx
Momentum in the -x-direction = -mUx
Change in momentum = 2mUx
Total time taken - from one end to the other and vice versa - = 2l / Ux
Rate of change in momentum = 2mu/(2l / Ux)
= mUx2/l
According to Newton's Second Law, the rate of change of momentum is the force exerted by the molecule on the wall.
Therefore, Force = [mUx / l]
Since pressure, P = force / area
Pressure on the wall, P = [mUx2/l] / l2
= mUx2 / l3
= mUx2 / V, where V is the volume of the container, THE cube.
If there are N molecules in the container,
P = m[U1x2 + U2x2 + U3x2 + ... + Unx2 ] / V
If the velocities are equal,
P = m[NUx2 ] / V
P = NmUx2 / V
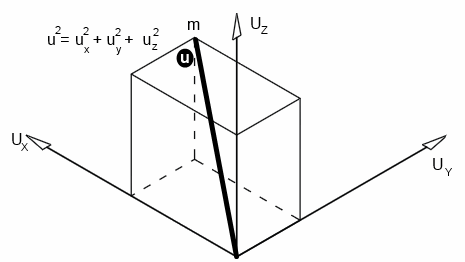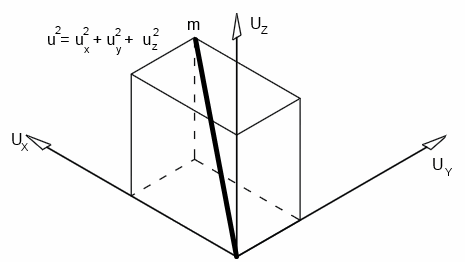
Since velocity in each direction is equal,
U2 = Ux2 + Ux2 + Ux2 = 3Ux2
Ux2 = U2 / 3
U2 is called the mean square velocity. Therefore, it is written as c2̄
Ux2 = c2̄ / 3
So, P = Nmc2̄ / 3V
PV = 1/3 mNc2̄
Since mN = mass of air molecules, mN / V = density = ρ
ρ = 3P / c2̄
Kinetic Energy of a Gas Molecule
The ideal gas equation shows PV = nRT, where n and R are the number of moles and Universal Gas Constant respectively.
1/3 mNc2̄ = nRT
mc2̄ = 3nRT / N
1/2 mc2̄ = 3nRT / 2N
KEmolecule = (3nR/2N) T
KEmolecule = k T
KEmolecule ∝ T
So, the kinetic energy - KE- of a gas molecule is directly proportional to the absolute temperature of the gas.
The following animation shows the connection between the KE and absolute Temperature(T).
Please click on the canvas to start / stop the animation.
E.g.1
Calculate the root mean square speed of five molecules:< / / / /br>
Five molecules of a gas have the following speeds (in meters per second): 20, 35, 42, 18, and 29. What is the root mean square speed of these molecules?
Square the speed of each molecule as follows:
- Molecule 1: 20² = 400
- Molecule 2: 35² = 1225
- Molecule 3: 42² = 1764
- Molecule 4: 18² = 324
- Molecule 5: 29² = 841
Now, find the average of the squared speeds:
- Add the squared speeds together: 400 + 1225 + 1764 + 324 + 841 = 4554
- Divide the sum by the number of molecules (5): 4554 / 5 = 910.8
Therefore, the root mean square speed of the five molecules is approximately 30.18 meters per second.
E.g.2
What is the average rms of a helium molecule inside a party balloon at 40°C?
For a helium molecule
1/2 mc²- = 3KT/2
c² = 3KT/m
rms = √3KT
- k is the Boltzmann constant (1.38 x 10^-23 J/K)
- T is the absolute temperature in Kelvin (convert 40°C to Kelvin: 40°C + 273.15 = 313.15 K)
- m is the molar mass of helium (4 g/mol) (convert grams to kilograms: 4 g/mol * (1 kg / 1000 g) = 4 x 10^-3 kg/mol)
rms = √(3 * (1.38 x 10^-23 J/K) * 313.15 K / (4 x 10^-3 kg/mol))
- Calculate the square root:
rms ≈ 1303 m/s
Therefore, the average root mean square speed of helium molecules at 40°C is approximately 1303 meters per second.
E.g.3
What would have happened to the rms, if the temperature of a helium balloon was doubled ?
If the temperature of the helium gas is doubled from 40°C to 80°C, the root mean square speed (RMS speed) of the helium molecules will also increase. Here's why:
The formula for RMS speed (v_rms) is:
v_rms = √(3kT / M) where:
- k is the Boltzmann constant (a constant value)
- T is the absolute temperature (in Kelvin)
- M is the molar mass of helium (which remains constant)
In this scenario, the temperature (T) is doubled. Since the square root function is proportional to its argument raised to the power of ½, doubling the temperature will have a greater than proportional effect on the RMS speed.
Here's the breakdown:
- Initial temperature (T1) = 313.15 K (40°C + 273.15)
- Doubled temperature (T2) = 2 * T1 = 626.3 K (80°C + 273.15)
Without calculating the exact values, we can see that:
- (T2) / (T1) = 2
Taking the square root of both sides:
- √(T2) / √(T1) = √2 (since the square root of 2 is approximately 1.41)
This means the RMS speed will be approximately multiplied by √2, which is an increase of roughly 41%.
To calculate the actual new RMS speed:
- New v_rms ≈ √(3k * 626.3 K / M)
Although we haven't explicitly calculated the new value, we know it will be higher than the initial 1303 m/s by a factor of approximately √2.
Energy of air molecules in action - Stirling Engine
The Stirling engine was invented in 1816 by Rev. Robert Stirling of Scotland. Unlike steam engines, the Stirling is a very simple engine, that works on the principle of expansion / contraction of a trapped mass of gas. It became popular with the industrialists in the 19th century before being shadowed by the advent of electric motor.
These engines have become popular again due to the miniature models promoted by science enthusiasts.I bought one recently and it was just magical to watch - pretty fast and elegant working.
The energy transferred by the lamp makes air expanding with increased kinetic energy, which triggers off the rest of the process.
This is how it works:
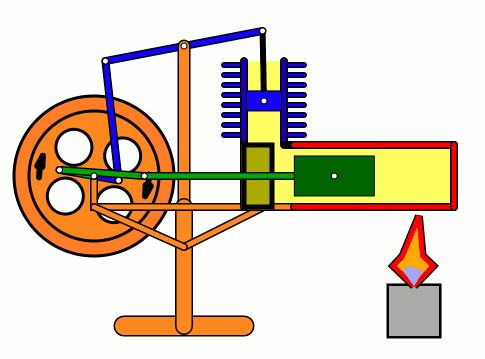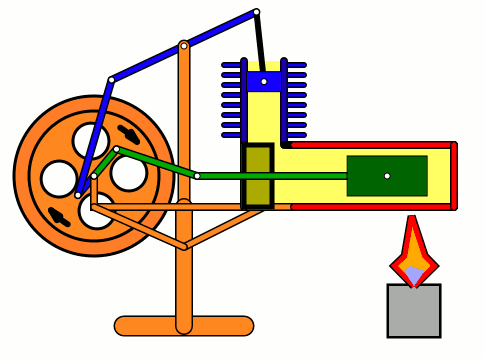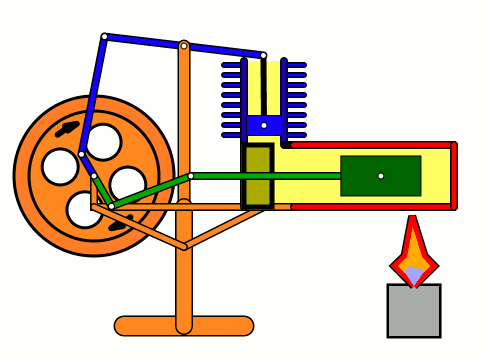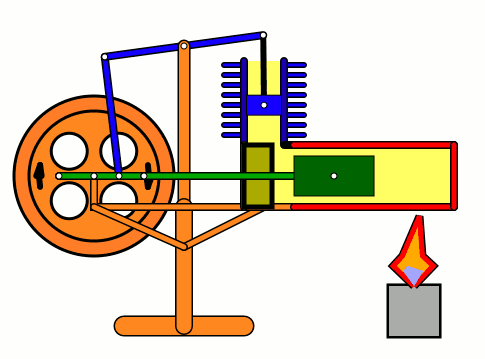
Don't use petrol as the fuel for the lamp - dangerous and inflammable; instead, you can use 90% strong rubbing alcohol.
A Quiz on Kinetic Theory of Gases