Terminal Velocity - speed - V_t

 

 

Force, mass and acceleration

When an object falls under gravity, three forces act upon it. They are the weight, drag force and upthrust. The weight acts downwards and the other two upwards, which result in a net force acting on the object towards the ground. Since F = ma, the object gains an acceleration.

The weight and upthrust of the object remain the same throughout the motion. The drag force, however, is changing with the speed of the object: the greater the speed, the greater the drag force.

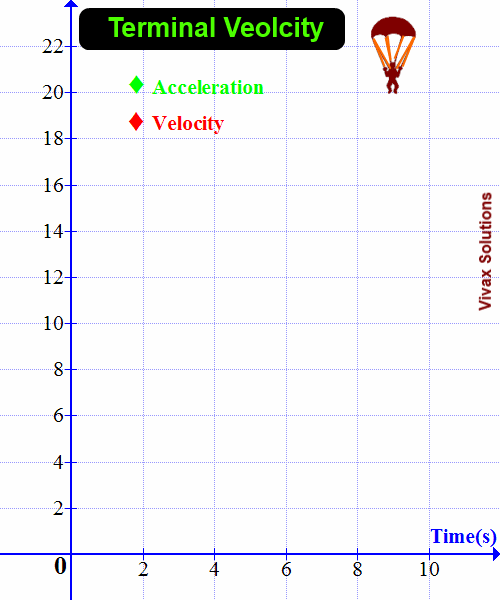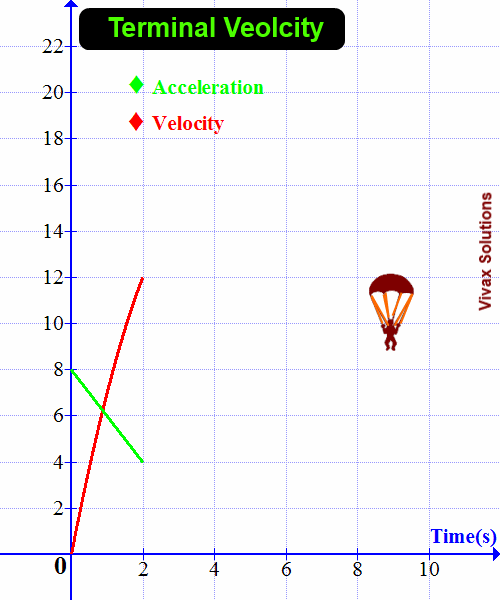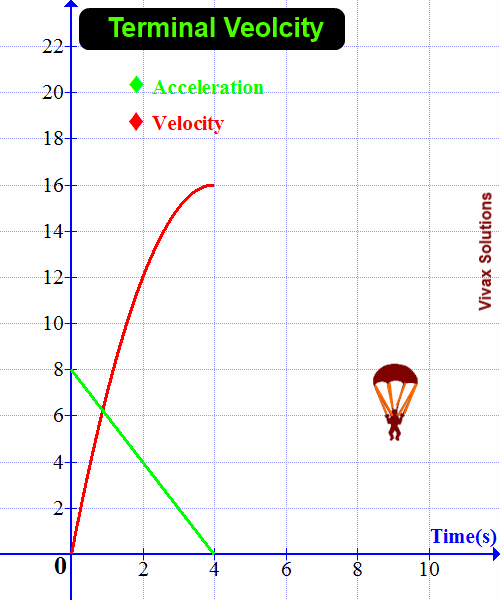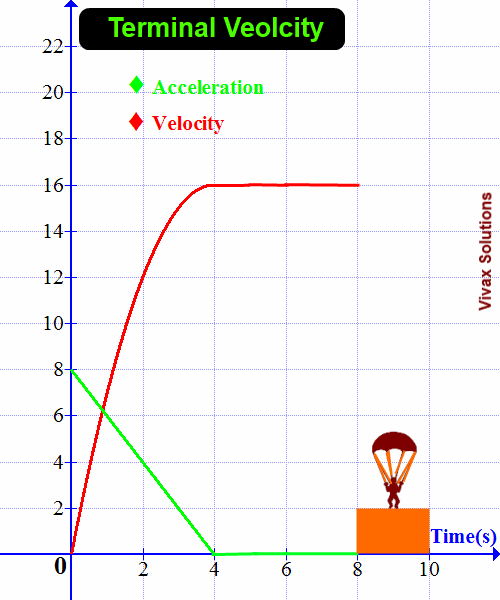
As the drag force increases with the speed, at a certain point, the total upward force and the downward force become equal. As a result, the net force is equal to zero. Since there is no net force - resultant force - the acceleration of the object, at that moment, becomes zero. Then, the object continues to move downwards at a constant velocity.

This is called the Terminal Velocity - V_t

Movement of a ball in a viscous fluid

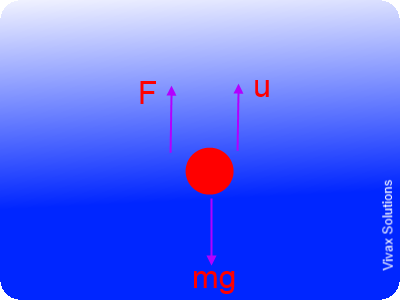
Consider the movement of a ball inside a viscous fluid:

1. Radius - r
2. Coefficient of Viscosity - η
3. Density of the ball - d
4. Density of the liquid - ρ
5. Acceleration due to Gravity - g

The ball is subjected to the influence of three forces: they are the weight, upthrust and the viscous force - drag or liquid friction.

Weight of the ball = mg = 4/3 πr³dg

Upthrust on the ball by the liquid = v ρ g = 4/3 πr³ ρg

According to Stokes Law,
Viscous force = 6πηV, where V is the velocity at a given a time.

At the outset, the downward force, weight, is greater than the combination of the upward forces. So, initially, the ball accelerates. The viscous force, which depends of the velocity, however, keeps increasing. As a result, at some point, the net force on the ball becomes zero and the velocity of the ball becomes constant.

It is the Terminal Velocity - V_t

When the balls moves at the terminal velocity,

4/3πr³d = 4/3πr³ρg + 6πηV_t

V_t = 2(d - ρ)gr² / 9η