Forms of Energy

Energy
The ability to perform work is defined as energy, in science.

There are various forms of energy:

• Sound
• Heat
• Electric Energy
• Light
• Kinetic Energy - energy due to movement
• Potential Energy - energy due to position
• Chemical Energy - energy stored in substances

 

Regardless of the type of energy, each of them is subjected to a universal law that is as follows.

Conservation of Energy

Energy cannot be created, nor can it be destroyed. It can only be transformed from one form to another.

E.g.

A microphone turns sound into electrical energy.
A speaker turns electricity into sound.
A light bulb turns electricity into light.
A solar panel turns light into electricity.

In the following animation, when the ball falls down, it loses the potential energy, which in turn becomes kinetic energy. A part of kinetic energy, then, becomes sound energy and heat.

E.g.

The mass of the above ball is 2kg and dropped from a height, 10m, from rest. When it hits the ground for the first time, it bounces back to a height, 8m. How do you account for the loss of height on first impact?

If the acceleration due to gravity is 9.8 ms^-2 and velocity on impact is v,
v² = u² + 2as
v² = 0 + 2 x 9.8 x 10 = 196
v = 14 m/s
If the kinetic energy of the ball before impact, KE
KE = 1/2 x 2 x 14² = 196 Joules
If the potential energy at the height, 8m, is PE,
PE = 2 x 9.8 x 8 = 156.8 Joules
The loss of energy due to impact = 196 - 156.8 = 39.2 Jouels
There is clearly a loss of energy due to impact. The loss of energy turns into sound and heat.
With each impact after the collisions with ground, the loss of energy becomes significant. That's why its bouncing height gets smaller with each hit with the ground.

Energy Sources

The sources of energy can be divided into two categories. They are,

• Renewable Sources - replenishing possible | E.g. solar energy, wind energy, geo-thermal energy, hydropower, biomass
• Non-renewable Sources - replenishing not possible | E.g. fossil fuels, nuclear energy, coal

 

The above sources can be used to produce both primary and secondary energies.
In Winter, at home we burn oil to produce heat - primary energy source.
At power stations, fossil fuels are burned in order to produce electricity from heat - primary and secondary energy sources in order.

Energy Generation in a Power Station - from a renewable source

In the following diagram, the mechanism of a hydroelectric power station is explained.
The water, stored in a reservoir, is brought down to the power station from a significant height. It loses its potential energy that in turn becomes the kinetic energy. The water then hits the turbines of the power generator, which in turn, rotates the armature of a set of coils, surrounded by strong magnets. During the process, kinetic energy turns into electrical energy through a process called electromagnetic induction
The electricity is then distributed across various parts of the country in question.

 

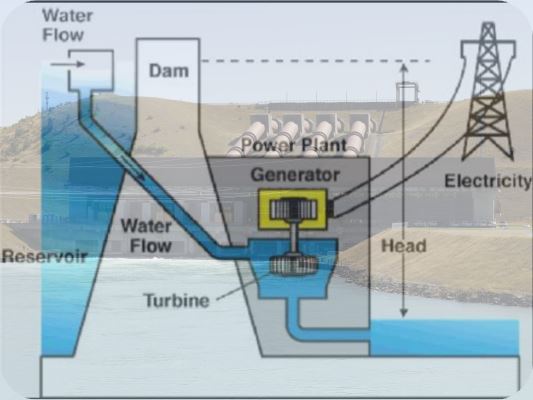
If you have ever been to a power station, you will realize the loss of energy in the form of sound; it's simply deafening! Despite this drawback, the hydroelectric power plants are very efficient - about 90%.

E.g.

For every 1kg of water that comes down through 10 m,
Loss of potential energy = 1 x 9.8 x 10 = 98 J
At 90% efficiency,
Electrical energy generated = 98 x 90/100 = 88 J.

Energy Generation in a Power Station - from a non-renewable source

In the following diagram, the mechanism of a nuclear power station is explained.
At the core of the nuclear reactor, there are radioactive fuel rods. When the radioactive reactions take place inside them, an enormous amount of heat is generated. The heat is then taken away by the flowing water, which in turn becomes pressurised steam. The steam is used to rotate the turbines of a generator to produce electricity.

 

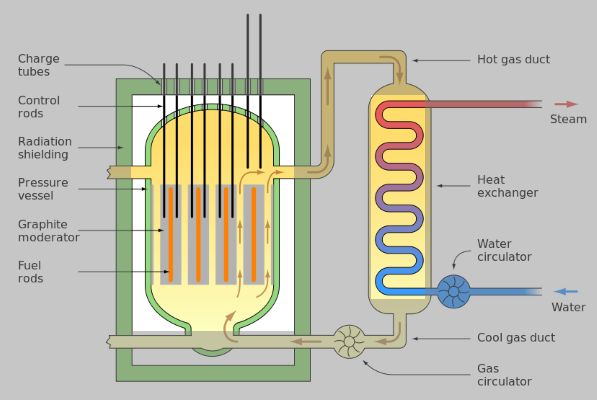
The control rods are lowered to slow down the nuclear reaction, if the activity goes up rapidly. The graphite moderators keep the velocity of radioactive particles at bay.
The nuclear power plants are very low in efficiency - about 33%. In addition, there is a serious risk of accidents and the monumental challenge of getting rid of used fuel rods that could stay radioactive for generations to come.
Moreover, it is very costly to build a nuclear power station.

images: credit:Wikipedia

Wind Turbine

Wind turbines are mushrooming across the world in proportion to our enthusiasm for renewable energy sources. They simply work on wind and the initial cost is relatively low - an encouraging factor to lure people to use them where wind is consistently abundant.

 

 

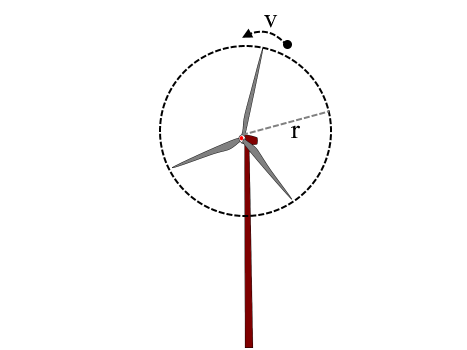
Wind turbines convert the kinetic energy of wind - KE - into electrical energy: the wind turns the blades in such a way the the latter activates a generator attached to the apex of the wind turbine; it's a simple energy converstion mechanism, indeed. The calculations are as follows:

If the speed of the wind is v and the radius of the rotor blade is r,
The cross sectional area of the path covered by the blades = π r²
The volume of air that passes through the blades in one second = πr² v
If the density of air is ρ,
The mass of air that passes through the blades in one second = ρ πr² v
The kinetic energy of this air, KE = 1/2 mv² = 1/2 ρ πr² v v² = 1/2 ρ πr² v³
The kinetic energy turns into the electrical energy of the wind turbine. A significant of the kinetic energy , however, turns into noise and heat - just wasted.
German physicist, Albert Betz, found out in 1919 that there was a maximum limit to this conversion; it's 59% of the kinetic energy. It's known as Betz' Limit.
The Betz' Limit, limits the power converted to electricity from the kinetic energy. It adds a power coefficient to the above equation, C_p.
Therefore, the available power is as follows:
P = 1/2 ρ πC_p r² v³
E.g.
v = 20 m/s; r = 20m; ρ = 1.23kg/m³ C_p = 0.2
Available power = 1/2 x 1.23 x 12² 20³ = 2.47 MW.

 

With the following interactive animation, you can see how wind speed changes the power available in a wind turbine; the greater the wind speed, the greater the available power, subjected to Betz' Limit.