Capacitors for A Level Physics

Dive into the World of Capacitors with Interactive Simulations

Capacitors: The Unsung Heroes of Electronics

Understanding capacitors is essential for mastering A-Level Physics. They're the unsung heroes behind countless electronic devices, from your smartphone to your laptop. But what exactly are they, and how do they work?

This interactive tutorial will guide you through the intricacies of capacitors. You'll explore key concepts like capacitance, energy storage, and how capacitors behave in different circuit configurations. Best of all, you'll get to experiment with real-world scenarios through our engaging simulations.

In this tutorial, you will learn:

 

What is a capacitor?

A capacitor is a device that stores charges - energy. They come in different shapes and sizes. A circuit board contains lots of them, as shown below. You may not know that the screen of your smartphone or tablet is a grid of hundreds of capacitors, which make the touching mechanism work smoothly.

 

A basic capacitor consists of two metal plates, separated by an insulating layer. A capacitor is charged by connecting it to a cell. The charging process is as follows:

 

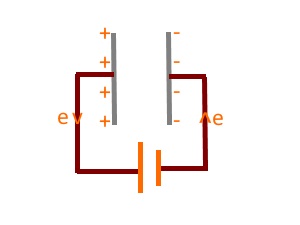
When the two plates are connected to a battery or cell, the electrons move from the negative terminal of the battery or cell and accumulate on the plate connected to that particular terminal. When this happens, the electrons on the other plate get repelled and move away from it, leaving it positively charged.
The process continues up until the potential of each terminal is equal to that of the metal plate attached to it.
At that point, the voltage between the two plates is the same as the EMF - or the terminal potential difference - of the battery or the cell.
Then we remove the battery along with the wires. The capacitor is said to be charged. A charged capacitor has a charge, +Q, on one plate and -Q on the other.
Now, please move the mouse over the image.
The charge is considered as Q. There is a voltage between the two plates too.
It has been observed that Q ∝ V
Q = KV => K=Q/V
K is called capacitance.

Capacitance of a Capacitor (C)

C = Q/V
The charge stored per unit voltage is defined as the capacitance of the capacitor.
Units:
C = Q/V = Coulomb/Volts = CV^-1 = farad (F)
1F = 10⁶μF - micro farad
1F = 10¹²pF - Pico farad

Factors that determine the capacitance

The capacitance of a capacitor is determined by three factors; they are as follows:
C = ε A / d

 

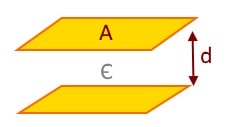
1. The greater the surface area, the greater the capacitance
2. The smaller the gap, the greater the capacitance
3. The greater the permittivity of the gap - ε- between the plates, the greater the capacitance

Although, the surface area of the plates and the distance between the plates can be used to increase the capacitance, they have a limited scope in real life: a large area takes up space in a circuit and a smaller gap may lead to short-circuiting. Therefore, the only feasible step is to increase the permittivity of the medium between the two plates. This is done by inserting glass, mica or even paper between the plates - the substances of high permittivity.

E.g.

The capacitance of a capacitor is 2 μF. Find its capacitance, if the distance between the plates is halved. What would be the capacitance, if the area of the plate was quadrupled?

C = εA/d
1) C' = εA/(d/2) = 2εA/d
= 4F - capacitance doubled
2) C' = ε4A/d = 4εA/d
= 8F - capacitance quadrupled

Energy Stored in a Capacitor

When a capacitor is connected to a battery or cell, charges accumulate on the plates. These charges move through a certain potential difference.
According to W = QV, the work done in the process, turns into the energy stored in the capacitor.

The voltage at the beginning = 0
Please move the mouse over the image.
The voltage at the end of charging = V
The average voltage = (0 + V)/2 = V/2
Work done = charge x voltage
W = Q X V/2
The work done turns into energy.
E = 1/2 QV
Since Q=CV,
E = 1/2 CV²
As V = Q/C,
E = 1/2 Q²/C

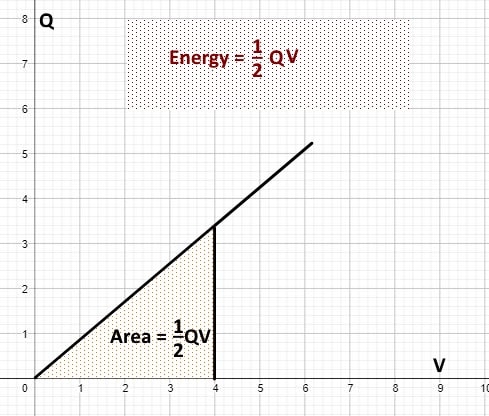
The energy stored in a capacitor is given by the area under the graph of Q against V.

E.g.1

The charge of a capacitor is 12C and the voltage between the plates is 5V. Find the energy stored in the capacitor.
E = 1/2 QV
= 1/2 X 12 X 5
= 30J

E.g.2

The capacitance of a capacitor is 6F and the voltage between the plates is 10V. Find the energy stored in the capacitor.
E = 1/2 CV²
= 1/2 X 6 X 100
= 300J

E.g.3

The charge of a capacitor is 60C and the capacitance is 3F. Find the energy stored in the capacitor.
E = 1/2 Q² / C
= 1/2 X 3600 /3
= 600J

Connecting Capacitors

In practice, we have to combine the capacitors to maximize their effect in circuits. This is done in two ways:

In series

- The charges of the capacitors are the same; the voltage splits up.

In parallel

- The voltages across the capacitors remain the same; but the charge splits up.

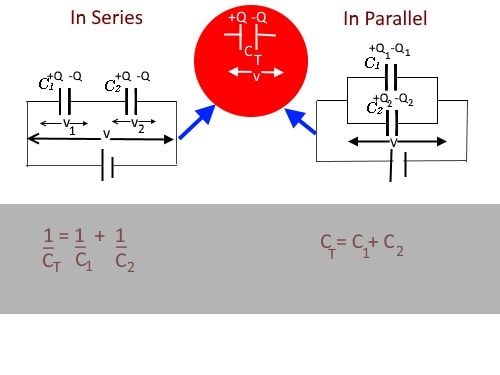Proof - capacitors in series:

v = v₁ + v₂
= Q/C₁ + Q/C₂
= Q[1/C₁ + 1/C₂]
If the capacitance of the capacitor that has the same effect at voltage v with charge Q is C_T,
v = Q/C_T
Q/C_T = Q[1/C₁ + 1/C₂]
1/C_T = 1/C₁ + 1/C₂

Proof - capacitors in parallel:

Q = Q₁ + Q₂
= C₁v + C₂v
= C₁v + C₂v
If the capacitance of the capacitor that has the same effect at voltage v with charge Q is C_T,
Q = C_Tv
C_Tv = C₁v + C₂v
C_T = C₁ + C₂

E.g.1

Find the total capacitance of the following circuit.

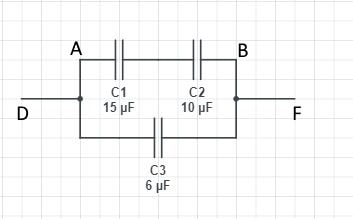
Between A and B,
1/C_Total = 1/C₁ + 1/C₂
= 1/15 + 1/10
C_Total = 6μF
Between D and F,
C_Total = C₁ + C₂
= 6 + 6 = 12μF

E.g.2

Find the total capacitance of the following circuit.

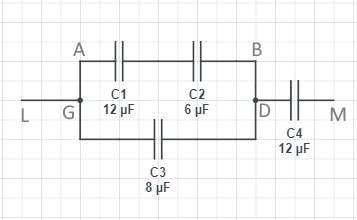
Between A and B,
1/C_Total = 1/C₁ + 1/C₂
= 1/12 + 1/6
C_Total = 4μF
Between G and D,
C_Total = C₁ + C₂
= 4 + 8 = 12μF
Between L and M,
1/C_Total = 1/C₁ + 1/C₂
= 1/12 + 1/12
C_Total = 6μF

E.g.3

Find the charge, voltage and the energy stored in each capacitor of the following circuit.

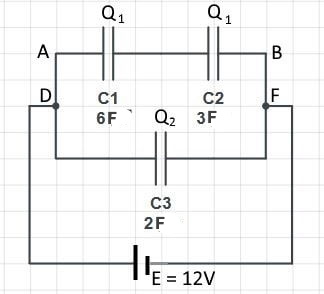
Between A and B,
1/C_Total = 1/C₁ + 1/C₂
= 1/6 + 1/3 = 3/6 = 1/2
C_Total = 2F
Between D and F,
C_Total = 2 + 2 = 4F
Since Q = CV,
Q_Total = 4 X 12 = 48C
Q₁ + Q₂ = 48C
Q₂/2 = 12 => Q₂ = 24C
Q₁ = 48 -24 = 24C
The charge in C1 and C2 are 12C each; the charge in C3 is 24C.
Voltage across C1 = 24/6 = 4V
Voltage across C2 = 24/3 = 8V
Voltage across C3 = 24/2 = 12V
E = 1/2 QV
Energy of C1 = 1/2 x 24 x 4 = 48J
Energy of C2 = 1/2 x 24 x 8 = 96J
Energy of C3 = 1/2 x 24 x 12 = 144J

E.g.4

The capacitance of a capacitor is 12F and connected to 3V supply for charging. Once charged, it was removed from the power source and then connected to a capacitor of capacitance, 6F, which has not been charged. Find the following:
1) The charge in each capacitor
2) The voltage across each capacitor
3) The energy of the first capacitor before being connected to the second
4) The total energy of the capacitors after being connected
5) The loss of energy, if any and the reason for it

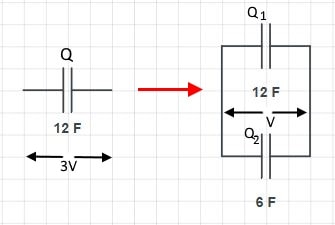
When the capacitors are connected, the charges are shared between the two up until the voltage is the same for both.
For the 12F capacitor,
Q = CV => Q = 12 X 3 = 36C
This charge is later shared by both - as there is no external power source.
1) Q₁ + Q₂ = 36
Since the two capacitors are in parallel,
Q₁ / 12 = Q₂ / 6
Q₁ = 2Q₂
2Q₂ + Q₂ = 36
3Q₂ = 36
Q₂ = 12C
Q₁ = 24C
2) v = Q₁/12 = Q₂/6
v = 24/12 = 2V
3) E = 1/2 X 36 X 3 = 54J
4) E₁ = 1/2 x 24 x 2 = 24J
E₂ = 1/2 x 12 x 2 = 12J
Total energy = 36J
5) The loss of energy = 54 - 36 = 18J
The energy is lost due to the movement of the charges through wires - the current - as heat.

E.g.4

A capacitor is charged with the aid of a cell. It is then disconnected from the power source and the gap between the two plates doubled. What will happen to the energy stored in the capacitor?

Since it is no longer connected to the power source, the charge, Q, remains constant.
C = εA/d
As d increases, C goes down
E = 1/2 Q² / C
Q is constant and C goes down;
The energy stored in the capacitor will go up.
An alternative proof:
Since the capacitor is disconnected from the power source, it cannot get energy from an external power source.
The plates have opposite charges and work must be done in order to move them apart.
The work done in turn becomes the stored energy; the energy stored in the capacitor goes up.

Combined Capacitors - interactive practice

Please move the sliders to change the capacitance of each capacitors and find the total capacitance interactively.

Discharging a Capacitor through an External Resistor

Suppose a capacitor is allowed to discharge across a resister. The voltage across can be measured through the voltmeter, once the switched is on.

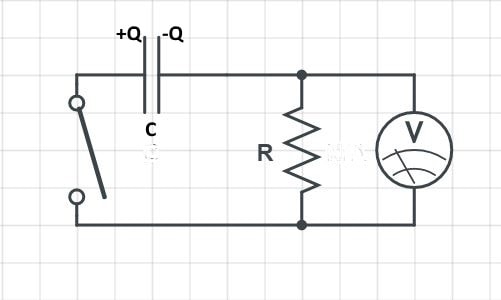
It has been observed that the rate of change of charge is proportional to the charge of the capacitor at a given time.
dQ/dt ∝ -Q ; considering as negative to reflect the charge being lost
This is an exponential relationship - the rate of change(dQ/dt) is proportional to the quantity(Q) in question.
dQ/dt = -kQ
1/Q dQ = -kdt
∫ 1/Q dQ = ∫ -kdt
ln(Q) = -kt + c
Q = e ^{-kt + c} = e ^-kt X e^c 1
When t = 0, Q = Q₀
Q₀ = e^c
From 1 => Q = Q₀ e ^-kt
The loss of charge takes the exponential form: the rate of loss of charge is the same during the same time intervals.
k = 1/RC, where R and C are resistance and the capacitance respectively.<
Q = Q₀ e ^-t/RC

The charge against time is an exponential curve - decay. The rate of loss is the same after each time period.
RC = Time Constant.

Significance of Time Constant

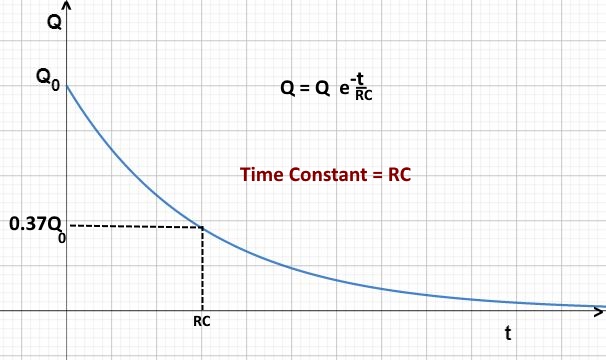
Q = Q₀ e ^-t/RC
When t = RC,
Q = Q₀ e ^-RC/RC
Q = Q₀ e ^-1
Q = Q₀ / e
Q = 0.37 Q₀
That means, the remaining charge of the capacitor after 1 time constant is 0.37 of the original charge.
In other words, the capacitor loses 63% of its charge or energy in 1 time constant.
Since the decay is exponential, during the next time constant, it will lose 63% of the remaining charge again - leaving it with 0.14 of the original charge.

Half Life - t_1/2

The time taken by the capacitor to lose a half of its initial charge is called the half life of the capacitor.

Q = Q₀ e ^-t/RC
If Q = Q₀/2; t = t_1/2 => Q₀/2 = Q₀ e ^-t_1/2/RC
1/2 = e ^{- t_1/2/RC}
e ^t_1/2/RC = 2
t_1/2/RC = ln(2)
t_1/2= ln(2)RC
t_1/2= 0.69RC
= 0.69 of the time constant.

You may practise the following applet to see the discharging in action; in the applet, I use the initial charge, Q₀, as 100C, R = 1Ω and C = 2F. Time constant = 2 x 1 = 2.
Please move the slider and experiment with it.

 

E.g.

The charge of a capacitor is 200 C and its capacitance is 4F. It is discharged through a resistor of 3Ω.
1) Find the time constant.
2) Find the half life.
3) Find the charge left after two half lives.
3) Find the charge left after three time constants.

1) RC = 4 X 3 = 12
2) t_1/2 = 0.69 x RC = 0.6 9 X 12 = 8.28s
3) 200 -> 100 -> 50; it's 50C
4) 200 -> 0.37x200 -> 0.37 x 0.37 x 200 -> 0.37 X 0.37 X 0.37 X 200 = 10.1C

Other Forms of Exponential Decay of a Capacitor

Q = Q₀ e ^-t/RC
:- t => Q/t = Q₀/t e ^-t/RC
I = I₀ e ^-t/RC
I = I₀ e ^-t/RC
x R => IR = I₀R e ^-t/RC
V = V₀ e ^-t/RC

E.g.

The initial voltage of a capacitor is 20V. It is being discharged through a resistor, 2 Ω. If the capacitance is 3F, find the voltage after 5 seconds.

v = v₀ e ^-t/RC
v = 20 X e ^-5/6
= 8.69 V

Charging a Capacitor

A capacitor can be charged with the aid of a battery using the following circuit.

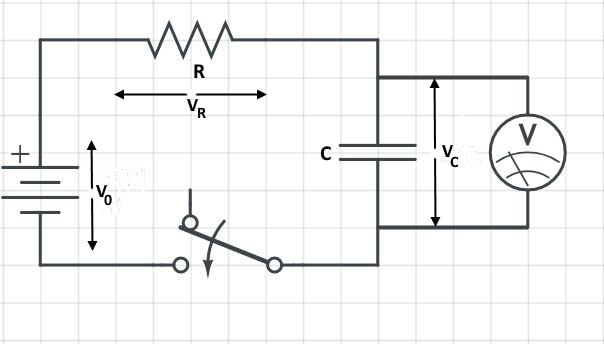
As soon as the switch is turned on, there is going to be a significant current - I₀ through the resistor - due to charges that reach the plates of the capacitor.
As the capacitor starts getting charged gradually, the current goes down and so does the voltage across the resistor - v = IR.
When the capacitor is fully charged, the current becomes zero and the voltage across the capacitor becomes the voltage across the battery. In other words, the voltage across the capacitor goes up and that of the resistor goes down.
V₀ = V_R + V_C
V₀ = IR + V_C
V_C = V₀ - IR
Since I starts going down from I₀ in an exponential way,
I = I₀e^-t/RC
V_C = V₀ - I₀Re^-t/RC
V_C = V₀ - V₀e^-t/RC
V_C = V₀(1 - e^-t/RC)
The change of V_R and V_C against the time is as follows:

When you move the Time slider, the voltage a,cross the capacitor increases and the voltage across the resistor decreases with the sum of them being unchanged. The resistance of the resistor is 1Ω and the capacitance of the capacitor is 4F - time constant = 4.

E.g.

A capacitor of capacitance 1F is connected in series to a resistor of resistance 4Ω; the pair is then connected to a battery of voltage 20V. Find the voltage across the resistor and the capacitor after 6 seconds.
Voltage across the resistor = V₀e^-t/RC = 20e^-6/4 = 4.46V
Voltage across the capacitor = V₀ - V₀e^-t/RC = 20e^-6/4 = 15.54V
You may verify these values with the above applet; just move the Time slider to 6 second position.

Energizing a Charged Particle

The following animation shows how a particle gets energized due to its motion across an electric filed: the vertical component of the velocity goes up, being accelerated in that direction while the horizontal component remains unchanged; the resultant velocity increases and so does the kinetic energy(KE).

You may use the two buttons to move and stop the electron.

Food for thought: what will happen to an electric charge when it enters a magnetic field? Will it be energized?

Uses of Capacitors in Real Life

Capacitors are extensively used in electronic circuits. Here are some of the uses:

1. The smartphone screen is essentially a grid of tiny capacitors. We change their capacitance by bringing our fingers closer to them, which in turn produces the electrical signals for the circuit.
2. The flash of a camera is powered by a capacitor. When a small charge stored in a capacitor is released in a very short period of time, according to I = Q/t, a significant current is produced, which leads to a large power. It creates the bright light.
3. Tuning condenser of a radio is a variable capacitor. By moving it, the capacitance is changed and the frequency of the radio station is then determined by the system.
4. Capacitors are used to smooth out the output, when an AC current is turned into a DC.
5. In electronic circuits, capacitors store energy to use up in power outages.

 

A Quiz on Capacitors for A Level