The Flow of an Electric Current

 

Transformation of energy at two ends...

 

 

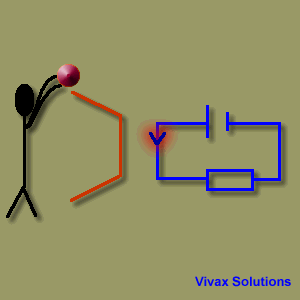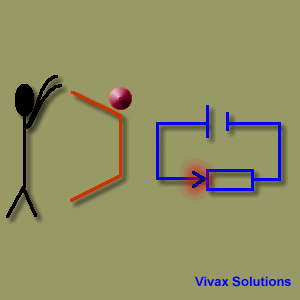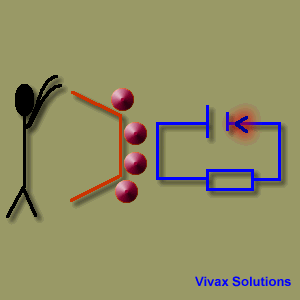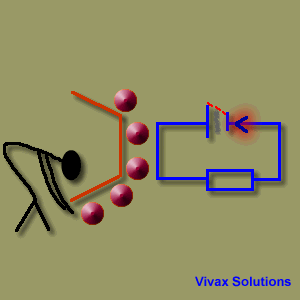
In an electric circuit, there is always a source of energy and a load. The former generates energy and the latter uses it up. The source can be a cell, battery, dynamo or even a solar panel. The load can be a resistor, a bulb, a fan or heater. We know while the energy transformations take place at the source and the load, an electric current flows through the circuit from a point of higher potential to that of lower potential.

In the above animation, the rolling balls mimic the electric current by going down from a point of high potential energy to a point of low potential energy. In the same way, the current, goes from positive terminal - at a higher potential - to the negative - at a lower potential. When the balls reach the feet of the man, however, they have to go from a point of lower potential energy to that of higher potential energy. This is not possible without the intervention of the man. Therefore, he bends down and picks them up to keep them moving by turning his chemical energy into potential energy.

When charges that carry the electric current reach the negative terminal of the cell, they face the same challenge. So, the chemical energy in the battery turns into electrical energy to provide the charges with energy to overcome the hurdle. That's why man gets tired and the battery runs down after some time, as their respective energies have turned into different forms.

Electro Motive Force - EMF

The amount of chemical energy that turned into electrical energy in order to move +1C along a circuit is called Electro Motive Force of the cell.

Units: Volts

Power of a Device

The energy used up by a device in a unit time is called its power.
Units:
P = E/t = J/t = Watts
If the voltage is V and the charge goes through it is Q in time t,
E = QV
So, P = QV/t = ItV/t = VI
P = VI
P = Watts; V = Volts; I = A

The power of a device must be given along with the voltage at which it is valid.
60W, 240V means, a power of 60W is produced at 240V.

E.g.1

The ratings of a bulb is 60W, 240V. Find its resistance.
P = VI
60 = 240I
I = 1/4 A
V = IR
240 = (1/4)R
R = 960Ω.

E.g.2

The ratings of an iron is 1200W, 240V. Find the current and the energy used up in an hour.
P = VI
1200 = 240I
I = 5A.
E = Pt
E = 1200 X 3600
E = 4.32x10⁶J.

E.g.3

The ratings of a bulb is 60W, 240V. Due to a power outage, the voltage drops down to 200V. Find the new power of the bulb. What would you notice in the bulb?
P = VI
60 = 240I
I = 1/4 A
V = IR
240 = (1/4)R
R = 960Ω
When working under new voltage
V = IR
200 = I x 960
I = 5/24 A
P = VI
P = 200 X 5/24
P = 41.7W
The bulb would get dimmer.

Evidence for the existence of internal resistance of a cell

 

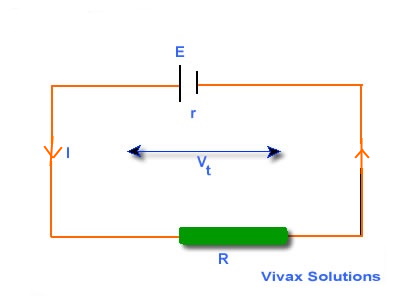
Suppose a charge Q travels along the circuit in time t. The EMF of the cell, the external resistance and the current are E, R and I respectively.
Energy produced by the cell = QE
Energy used up by the external resistor = QV_t
In practice, it has been noted QV_t < QE
Therefore, we have to account for the loss of energy, other than which occurred at the external resistor. It is certainly caused by the resistance present in the cell. It is called internal resistance(r).
So the new energy equation becomes,
QE = QV_internal + QV_external
Since Q = It and V=IR => ItE = Irt + IRt
E = Ir + IR
E = I(r + R)
IR = E - Ir
This is the potential difference across the external resistor (load). Since a voltmeter connected across a cell shows this up, instead of the EMF, it is known as the Terminal Potential Difference - V_t.
So, V_t = E - Ir
In an open circuit, I = 0. Therefore,
V_t = E.

E.g.

The EMF of a cell is 12V and its internal resistance is 2Ω. Find the current and the terminal potential difference across the cell, if it is connected to 4Ω external resistor.
E = I(R+r)
12 = I(4 + 2)
I = 2A
V_t = E - Ir
V_t = 12 - 2x2 = 8
V_t = 8V.

Connection of Cells

Cells can be connected in series or in parallel or a combination of both.

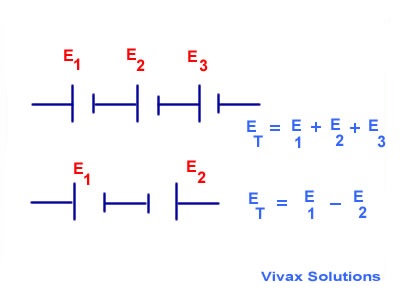
Connection in Series

The cells are connected in such a way that the current through each one is the same.

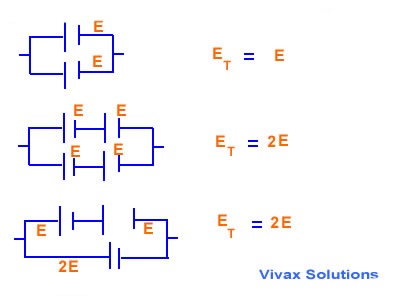
Connection in Parallel

The cells of EMF are connected in such a way that an equal current passes through each one.

Connection of Resistors

 

Resistors in Series

If resistors are connected in such a way that the current through each one of them is the same, they are said to be in series.

 

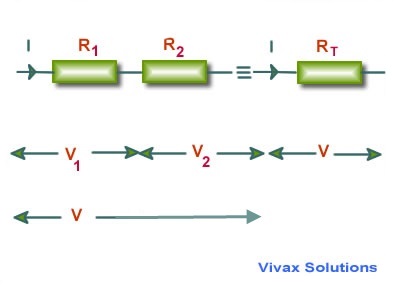
The single resistor that could substitute the combination, must produce a voltage V, when the current through it is I.
For the individual resistors, V = V₁ + V₂
V = IR₁ + IR₂
V = I(R₁ + R₂)
For the equivalent resistor - the substitute,
V = IR_T
IR_T = I(R₁ + R₂)
R_T = (R₁ + R₂)

Resistors in Parallel

If resistors are connected in such a way that the voltage across them is the same, they are said to be in parallel.

 

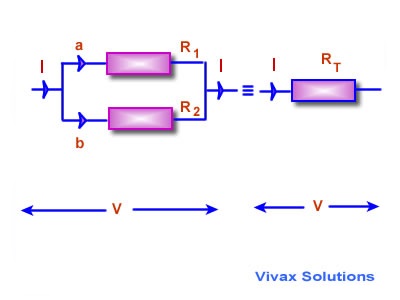
The single resistor that could substitute the combination, must produce a voltage V, when the current through it is I.
For the individual resistors, I = a + b
I = V/R₁ + V/R₂
V = V(1/R₁ + 1/R₂)
For the equivalent resistor - the substitute,
I = V/R_T
V/R_T = V/(1/R₁ + 1/R₂)
1/R_T = 1/R₁ + 1/R₂

E.g.1

Find the total resistance of the following circuit.

 

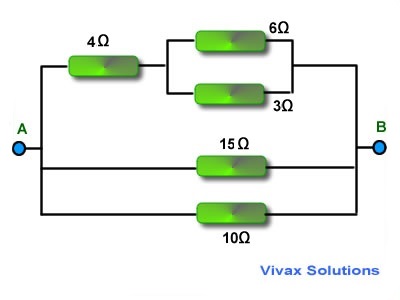
Total resistance across xy:
1/R_T = (1/ 6) + (1/3)
1/R_T = (1 + 2)/6 = 2/6 = 1/2
R_T = 2Ω
Total resistance of the branch = 2 + 4 = 6Ω
Total resistance of the three branches which are now in parallel
1/R_T = (1/ 6) + (1/15) + (1/10)
1/R_T = (5 + 2 + 3)/30 = 10/30 = 1/3
R_T = 3Ω

E.g.2

When two resistors are connected in series, the total resistance is 25Ω. If they are connected in parallel, the total resistance is 6Ω. Find the resistance of each.
When they are in series,
R_T = x + y = 25Ω
When they are in parallel,
1/R_T = (1/ x) + (1/y)
1/R_T = (x + y)/xy = 1/6
6(x + y) = xy
6 X 25 = xy => xy = 150 => x = 150/x
So, 150/x + x = 25
x² + 150 = 25x
x² - 25x + 150 = 0
(x - 15)(x - 10) = 0
x = 15 or x = 10
The resistance of each resistor is 15Ω or 10Ω

E.g.3

Find the total resistance of the following circuit and the current.

 

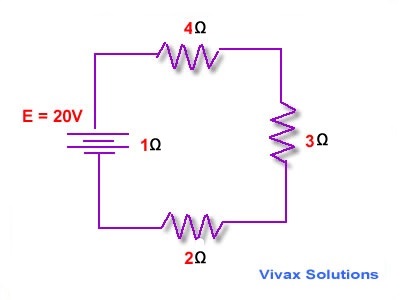
Since all the resistors are in series, total resistance is as follows:
R_T = 1 + 2 + 3 + 4 = 10Ω
Total Current = 20/10 = 2A
This current flows through each resistor, as they are in series.

E.g.4

Find the total resistance of the following circuit and the currents through each branch.

 

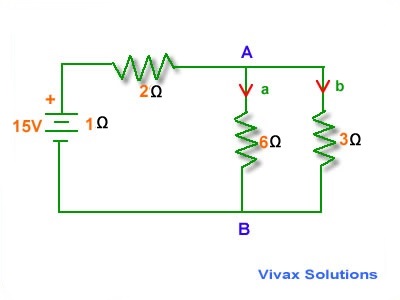
Total resistance across AB:
1/R_T = (1/ 6) + (1/3)
1/R_T = (1 + 2)/6 = 2/6 = 1/2
R_T = 2Ω
Total resistance of the circuit = 2 + 2 + 1 = 5Ω
Total Current = 15/5 = 3A
This current splits up at A, in inverse proportion to the resistance of each branch - the greater the resistance, the smaller the current that goes through it.
Since the two resistances are in parallel,
6a = 3b
b = 2a
a + b = 3
3a = 3 => a=1A ; b = 2A.
Other resistors get a current of 3A.

Advanced Questions on resistors in circuits

Find the total resistance of the following circuits:

 

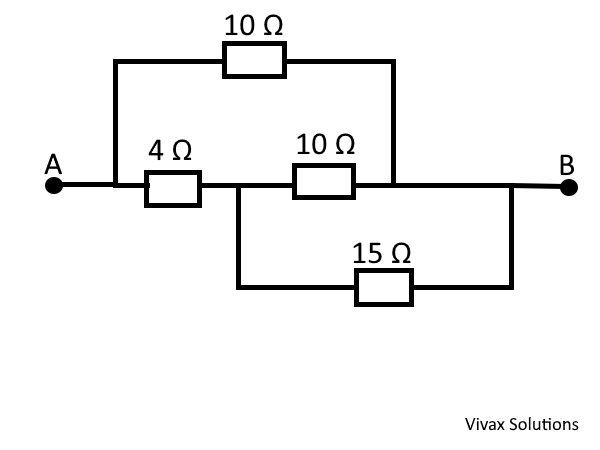
Ans:5 Ω

 

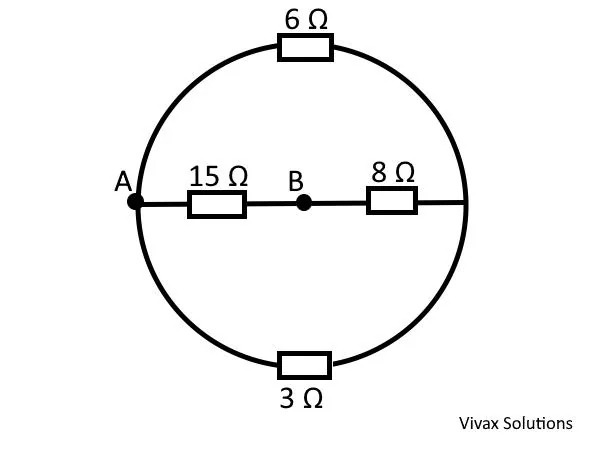
Ans:6 Ω

You can practise the calculations involving the resistors in series and parallel here. Just move the sliders and see how the total resistance changes.

 

Next Previous