Zhuravskii Formula for Shear Stress

What you learn from this tutorial involving Zhuravskii Formula:

Shear Stress

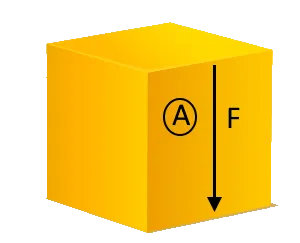
A shear force acts on a beam perpendicular to its main axis. The shear force causes shear strain along a plane as shown above. Shear stress, τ, at a given point is defined as follows:
τ = F/A, where F and A are the sheer force and the area of the cross section respectively.
Shear stress, however, is changing as you go from the top to the bottom; it’s not a constant.
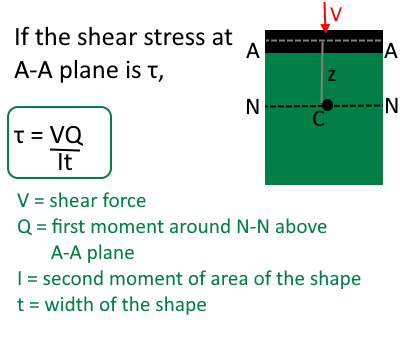
Zhuravskii Formula helps us find the shear stress at a given point — or level.

Dmitri Ivanovic Zhuravskii

Dmitri I Zhuravskii (1821–1891) was a Russian civil engineer who came up with the famous Zhuravskii Formula for calculating shear stress. He had been instrumental in developing railway lines, canals and cathedrals in his hey day in Russia.
For his yeomen services to the field of engineering, Zhuravskii was awarded the prestigious Demidov Prize in 1855 by the Russian Academy of Sciences.

Zhuravskii Formula

Zhuravskii Formula is an important mathematical tool for civil and mechanical engineers, when dealing with shear stresses that develop in the objects such as beams and columns.

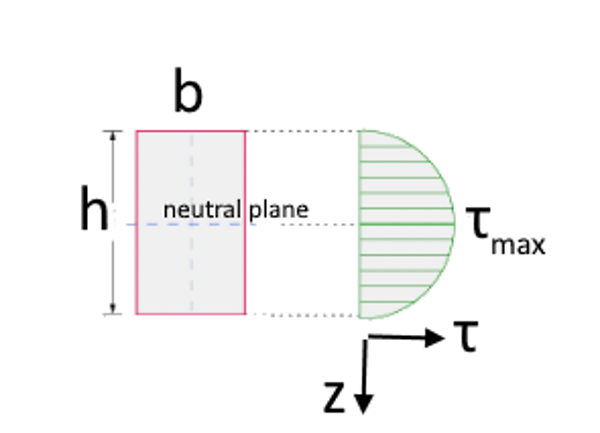
Case 1:

Zhuravskii Formula for a rectangular cross section

 

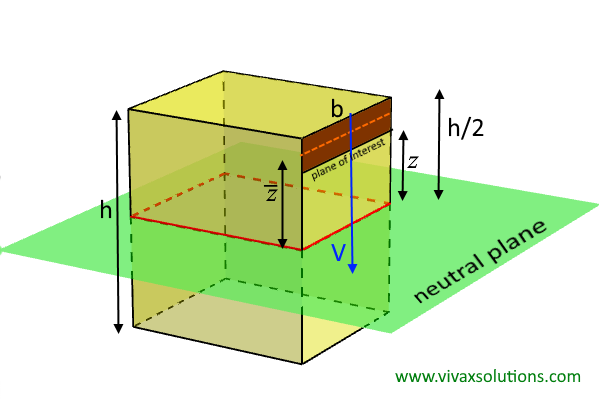
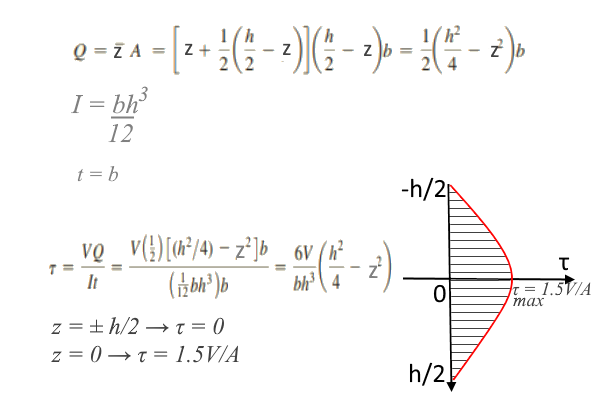
As you can see, the shear stress is maximum at the neutral plane. As you go towards the edges, the top or the bottom, it is going down and becoming zero. It is determined by the area — above or below the plane of interest.

With the following interactive simulation, you will be able to fully grasp the concept. Calculations are involved and update automatically. You will find it really useful to understand the nitty-gritty of the great mathematical tool.

Finding the average shear stress - τ_avg

We can use Simpson's Rule to find the average shear stress on the rectangular cross section. If there are just three strips, top, the middle and the bottom, the average shear force can be worked out as follows:

Area = ∫ Δx/3[τ_top + 4τ_middle + τ_bottom]
τ_avg = ∫ 1/6A[τ_top + 4τ_middle + τ_bottom]
= ∫ 1/6A[τ_top + 4τ_middle + τ_bottom]
= ∫1/6A[0 + 4x1.5V + 0]
= 6V/6A
= V/A
= Shear force / area of the rectangular cross section - as expected

Zhuravskii Formula: rectangular cross section - fully interactive simulation

You can practise the above fully interactively with the following simulation: you change the value of z, and Q so that V will be automatically updated.

Case 2:

Using Zhuravskii formula for a trapezoid — trapezium - cross section

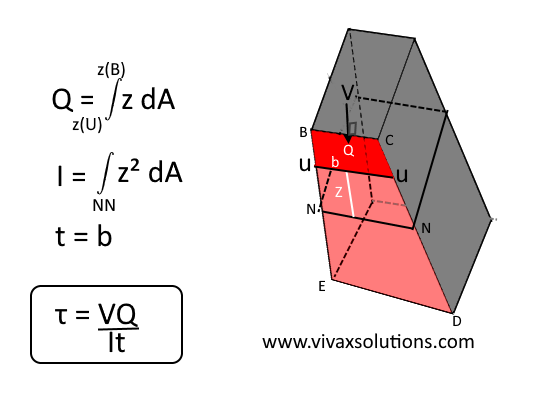
In this case, Q, the area above the plane of interest, UU, must be found by integration.
In addition, in order to calculate I, the moment of inertia for the surface around the neutral axis, NN, the parallel axis theorem must be used. Unlike in the case of a rectangular cross section, the width of the plane, t, changes too with z.
The above three unknowns can be calculated by simple integration and some algebraic calculations.
The process can be repeated even if the plane of interest, UU, is below the neutral plane, NN. The area, however, is the area under UU, right up to the bottom edge of the cross section.

Zhuravskii Formula: trapezoidal cross section - fully interactive simulation

You can practise the above fully interactively with the following simulation: you change the value of z, and Q so that V will be automatically updated.

Worked Examples

E.g.1

Derive an expression for the first moment of area of a rectangular lamina around the its base.

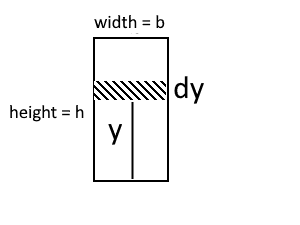
ȳ = ∫₀^h y dA / A_total
ȳ = ∫₀^h yb dy / A_total
ȳ = b/A_total[y²/2]₀^h
ȳ = bh²/2bh
ȳ = h/2

E.g.2

Derive an expression for the second moment of area of a rectangular lamina around the its base.

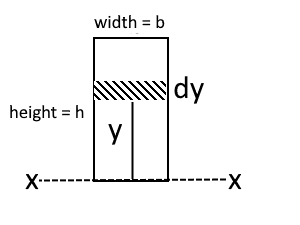
I_XX = ∫₀^h y² dA
I_XX = ∫₀^h y²b dy
I_XX= b[y³/3]₀^h
I_XX = bh³/3

E.g.3

Derive an expression for the second moment of area of a rectangular lamina around the neutral axis - the line through the centroid.

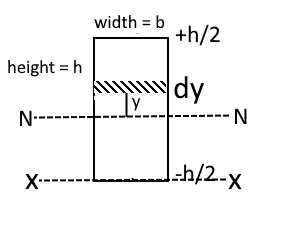
I_NN = ∫_-h/2^h/2y² dA
I_NN = ∫_-h/2^h/2y²b dy
I_NN= b[y³/3]_-h/2^h/2
I_NN = bh³/24 + bh³/24
I_NN = bh³/12

E.g.4

Using the formula for the second moment of area around the centroid, derive the same around the base with the aid of the Parallel Axis Theorem.

According to the parallel axis theorem, I_XX = I_NN + Ad²
I_XX = bh³/12 | A = bh | d = h/2
I_XX = I_NN + Ad²
I_XX = bh³/12 + bh(h/2)² = bh³/12 + bh³/4 = bh³/12 + 3bh³/12 = 4bh³/12
I_XX = bh³/3

E.g.5

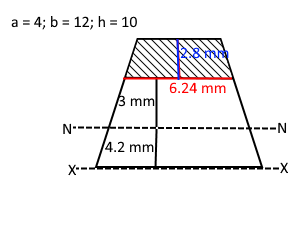
The height and the parallel sides of a trapezium are 10 mm, 4 mm and 12 mm respectively. Calculate the shear stress of a point that is 3 mm above the neutral plane.

For the entire trapezium,
ȳ = (h/3)(2a + b)/(a + b)
= (10/3)(8 + 12)/(4 + 12)
= 4.2
The neutral line passes through the centroid at 4.2 mm from the base.
I_XX = (h³/12)(3a + b)
I_XX = (10³/12)(12 + 12)
I_XX = 1000
From Parallel Axis Theorem,
I_XX = I_NN + Ad²
I_XX = 2000 | A = 80 | d = 4.2
2000 = I_NN + 80 x 4.2²²
I_NN = 611
The length of the plane of interest - shaded area = 6.24 - using similar triangles
Shaded area = (2.8/2)(4 + 6.24) = 14.3
Distance to the centroid of shaded area = 3 + 1.4 = 4.4
Q = ȳA = 4.3 x 14.3 = 61.5
τ = VQ/It
V = 120 Q = 61.5 I = 611 t = 6.24
τ = 120 x 61.5 /(611 x 6.24)
τ = 1.94 units

E.g.6

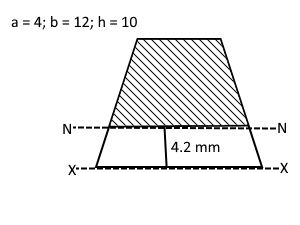
The height and the parallel sides of a trapezium are 10 mm, 4 mm and 12 mm respectively. Calculate the maximum shear stress of the cross section, taking into account the area above the neutral axis.

For the entire trapezium,
ȳ = (h/3)(2a + b)/(a + b)
= (10/3)(8 + 12)/(4 + 12)
= 4.2
The neutral line passes through the centroid at 4.2 mm from the base.
I_XX = (h³/12)(3a + b)
I_XX = (10³/12)(12 + 12)
I_XX = 1000
From the Parallel Axis Theorem,
I_XX = I_NN + Ad²
I_XX = 2000 | A = 80 | d = 4.2
2000 = I_NN + 80 x 4.2²²
I_NN = 611
The length of the plane of interest - shaded area = 8.64 - using similar triangles
Shaded area = (5.8/2)(4 + 8.64) = 36.7
Distance to the centroid of shaded area = 7.1
Q = ȳA = 2.5 x 36.7 = 93.4
τ = VQ/It
V = 120 Q = 93.4 I = 611 t = 8.64
τ = 120 x 93.4 /(611 x 8.64)
τ = 2.12 units

E.g.7

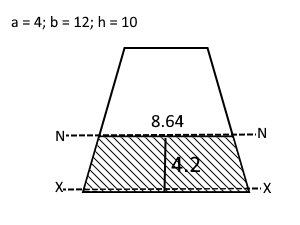
The height and the parallel sides of a trapezium are 10 mm, 4 mm and 12 mm respectively. Calculate the maximum shear stress of the cross section, taking into account the area below the neutral axis. Hence comment on the answers in e.g. 6 and e.g.7.

For the entire trapezium,
ȳ = (h/3)(2a + b)/(a + b)
= (10/3)(8 + 12)/(4 + 12)
= 4.2
The neutral line passes through the centroid at 4.2 mm from the base.
I_XX = (h³/12)(3a + b)
I_XX = (10³/12)(12 + 12)
I_XX = 1000
From the Parallel Axis Theorem,
I_XX = I_NN + Ad²
I_XX = 2000 | A = 80 | d = 4.2
2000 = I_NN + 80 x 4.2²²
I_NN = 611
The length of the plane of interest - shaded area = 8.64 - using similar triangles
Shaded area = (4.2/2)(12 + 8.64) = 43.3
Distance to the centroid of shaded area = 2.3
Q = ȳA = 2.3 x 43.3 = 99.7
τ = VQ/It
V = 120 Q = 99.7 I = 611 t = 8.64
τ = 120 x 99.7 /(611 x 8.64)
τ = 2.2 units
The two values in e.g.6 and e.g.7 are approximately equal, confirming the fact that maximum shear stress occurs close to the neutral axis.

Food for thought:

The above wooden beam has been subjected to shear forces. How do you account for the splitting closer to the middle axis?

E.g.8

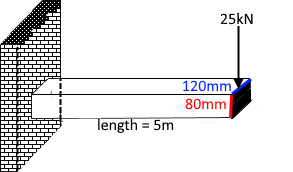
A cantilever beam is fixed to a wall. Its length is 5m and the dimensions of the cross section are 120mm and 80mm. A force of 25 kN is applied at the free end as shown below. Calculate the sheer stress at the following points from the top of the cross section. Hence find the maximum shear stress and point where it takes place at. Sketch a graph to show how the shear stress varies with the distance from the top, clearly showing the maximum stress.

1. 20mm
2. 40mm
3. 60 mm
4. 70 mm

τ = VQ/It
For a rectangular cross section, τ = (6V/bh³)(h²/4 - z²)
(6V/bh³) = 2.44x10⁹ | h²/4 = 1.6x10^-3
1) z = -20 → z² = 4x10^-4
τ = 2.93 MPa
2) z = 0 → z² = 0
τ = 3.9 MPa
3) z = 20mm → z² = 4x10^-4
τ = 2.93 MPa
4) z = 30mm → z² = 9x10^-4
τ = 1.7 MPa
Maximum sheer stress = 3.9 MPa; it occurs, when z = 0.