Modelling with Quadratics
Many real life situations or events can be modelled pretty accurately by mathematics formulae.
For instance, the tidal height of the River Thames that flows through London Suburbs has been modelled by a simple variation of the sine cure, which takes the following shape:
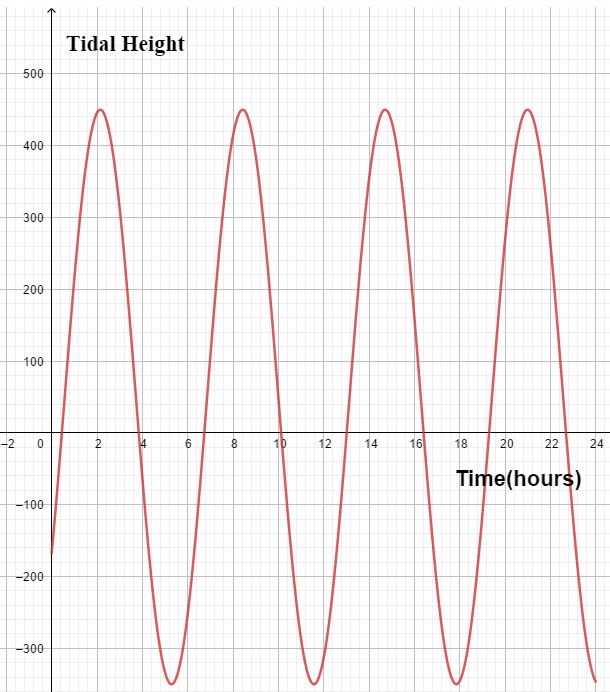
In the same way, the motion of a projectile can easily be modelled by a quadratic relationship.
In the following animation, a stone, thrown down from a cliff, is modelled by a quadratic equation - height against time. You can change the time and see how the height changes with it.
h(t) = 12 - t2/8, where h(t) is the height when time is t.
Modelling with Quadratics - worked examples
E.g.1
The height of a ball, dropped from a tree top, is modelled by the equation, h(t) = 625 - t2/25. Find the following:
- The significance of the number 625
- Time taken by the ball to drop by 4 metres
- Time taken by the ball to hit the ground
- h(t) = 625 - t2/25
h(o) = 625
It's the height of the tree.
- h(t) = 625 - t2/25
621 = 625 - t2/25
4 = t2/25
t2 = 100
t = ± 10
Since t is positive, t = 10 seconds.
- h(t) = 625 - t2/25
h(t) = 0
625 - t2/25 = 0
t2 = 625 x 25
t = ± 125 seconds.
Since t is positive, t = 125 seconds.
E.g.2
An arrow was thrown from the top of a hill; its height can be modelled by, h(t) = -4t2 + 16t + 80. Find the following:
- The height of the hill
- Time taken by the arrow to reach maximum height
- Time taken by the arrow to be at a height of 90 from the hill
- Time taken by the arrow to hit the ground
- h(t) = -4t2 + 16t + 80
h(o) = 80
It's the height of the hill.
- h(t) = -4t2 + 16t + 80 = -4[t2 - 4t - 20] = -4[(t - 2)2 - 24] = 4(t - 2)2 + 96
By the completing the square, when the height it maximum, t = 2. The corresponding height = 96 metres.
- h(t) = -4t2 + 16t + 80
h(t) = 90
-4t2 + 16t + 80 = 90
-4t2 + 16t - 10 = 0
t = 0.8 seconds or t = 3.2 seconds.
-
h(t) = -4t2 + 16t + 80
-4t2 + 16t + 80 = 0
t = -2.8 or t = 6.8
t = 6.8 seconds.