Polygons
A polygon is a closed shape with many sides.
E.g. triangle, square, rhombus, decagon
In this tutorial, you are going to see how the interior angles and exterior angles vary in polygons, depending on the number of sides. You can choose the number of sides of a polygon and see how the interior and exterior angles change.
The Sum of Interior Angles
The sum of interior angles of a polygon, T, is given by,
T = (n-2)(180, where n is the number of sides.
Based on the following image, you can see that there is a connection between the number of triangles in a polygon and the sum of interior angles of the polygon.
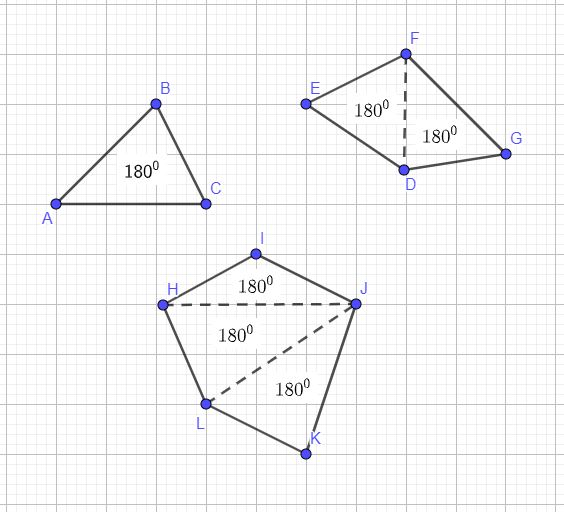
| Polygon | No of Sides | No of Triangles Inside | Sum of Interior Angles |
|---|
| Triangle | 3 | 1 | 1 x 180 |
| Square | 4 | 2 | 2 x 180 |
| Pentagon | 5 | 3 | 3 x 180 |
| Hexagon | 6 | 4 | 4 x 180 |
| Heptagon | 7 | 5 | 5 x 180 |
| Octagon | 8 | 6 | 6 x 180 |
| Nonagon | 9 | 7 | 7 x 180 |
| Decagon | 10 | 8 | 8 x 180 |
If the sides of a polygon are equal, it is called a regular polygon. In a regular polygon, the interior angles are equal.
The Sum of Exterior Angles
The angle between a side and the the extended adjacent side is called exterior angle.
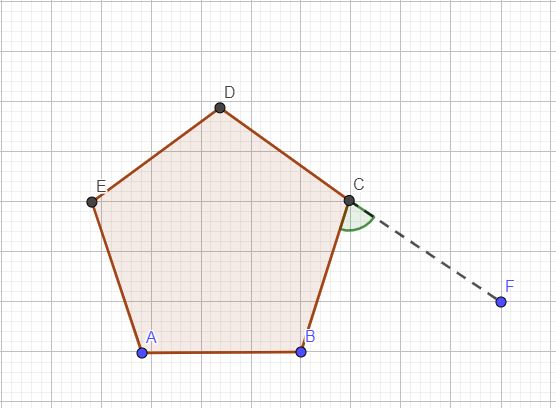
The sum of exterior angles add up to 3600. For a regular polygon of sides n,
Exterior angle = 360 / number of sides
Polygon Maker - interactive practice
With the following applet, you can practise interior and exterior angles of a polygon.