Logarithms

Exponential Functions

A function in the form of y = a^x, where a >= 1 is called an exponential function.

E.g.

y = 2^x; y = 3^x

The following image shows the nature of two exponential functions:

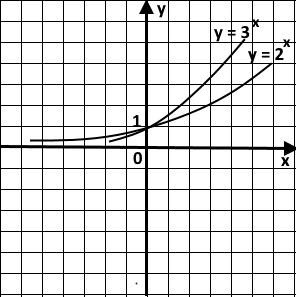
Exponential functions show the following features, regardless of the number:

• They go through (0,1) on a grid.
• For a small increase in x, there is a steep increase in y - hence, the change becomes exponential.
• As x approaches negative infinity, y approaches 0 - creating an asymptote.
• The values of the functions remain positive, regardless of the value of x.

The Exponential Function - e^x

This is a special exponential function, which is widely used in mathematics. It's special, because the gradient of the curve at any point is the same as the value of the function at the same point. It's still an exponential function, because it shows all the features that we discussed before.

The following image shows this feature:

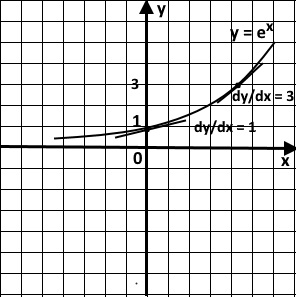
The Exponential Function - e^x - and the Natural Logarithm Function - ln(x)

The following image shows the exponential function and the natural logarithm function on the same grid. You can see they are closely related and worth studying together.

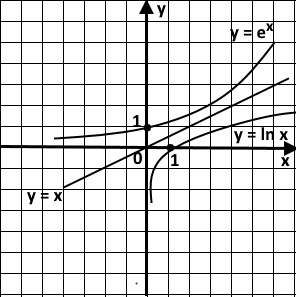
The following features can be seen in the two graphs:

• They swap around x and y values - e⁰ = 1; ln(1) = 0.
• They are symmetrical around y = x line.
• ln(x) is not defined for x = 0 or negative x values.
• The values of the function ln(x) can be positive, negative or even 0.

Logarithms

Consider the following indices and how they produce the corresponding logarithm values:

8² = 64 => we say that log₈64 = 2; - this is read as log 64 to the base 8 is 2.

4³ = 64 => we say that log₄64 = 3; - this is read as log 64 to the base 4 is 3.
Note the positions of the bases and indices in each case.

You may have noticed that in both cases the function is log(64), yet the values are different, because of the different bases. It shows the significance of the base, when it comes to dealing with logarithms. In short, log without a base is like a laptop without a keypad! The base is really important in logarithms.

In theory, a logarithm function can take any base value; the most used bases, however, are 10 and e.
log₁₀x = log(x) or lg(x); log_ex = ln(x);

Let's solve some problems involving logarithms now; the following approach is highly recommended to master this topic:

E.g.1

Find the value of log₃27
Let log₃27 = x
3^x = 27
Now write down 27 in index form with the same base.
3^x = 3³
So, x = 3.
log₃27 = 3.

E.g.2

Find the value of log₂32
Let log₂32 = x
2^x = 32
Now write down 32 in index form with the same base.
2^x = 2⁵
So, x = 5.
log₂32 = 5.

E.g.3

Find the value of log₁₀100
Let log₁₀100 = x
10^x = 100
Now write down 100 in index form with the same base.
10^x = 10²
So, x = 2.
log₁₀100 = 2.

E.g.4

Find the value of log₂2
Let log₂2 = x
2^x = 2
Now write down 2 in index form with the same base.
2^x = 2¹
So, x = 1.
log₂2 = 1.

E.g.5

Find the value of log₃1
Let log₃1 = x
3^x = 1
Now write down 1 in index form with the same base.
3^x = 3⁰
So, x = 0.
log₃1 = 0.

E.g.6

Find the value of log₂1/2
Let log₂1/2 = x
2^x = 1/2
Now write down 1/2 in index form with the same base.
2^x = 2^-1
So, x = -1.
log₂1/2 = -1.

E.g.7

Find the value of log₄8
Let log₄8 = x
4^x = 8
Now write down both 4 and 8 in a common base, such as 2, in index form.
(2²)^x = 2³
2^2x = 2³
So, 2x = 3.
x = 3/2
log₄8 = 3/2.

E.g.8

Find the value of log₃₆6
Let log₃₆6 = x
36^x = 6
Now write down both in index form with the base 6.
36^x = 6¹
(6²)^x = 6¹
So, 6^2x = 6¹
2x = 1 => x = 1/2
log₃₆6 = 1/2.

E.g.9

Find the value of log_0.254
Let log_0.254 = x
0.25^x = 4
Now write down both in index form with the base 4.
(1/4)^x = 4¹
(4^-1)^x = 4¹
So, 4^-x = 4¹
-x = 1 => x = -1
log_0.254 = -1.

E.g.10

Find the value of log₁₆8
Let log₁₆8 = x
16^x = 8
Now write down both in index form with the base 2.
(2⁴)^x = 2³
So, 2^4x = 2³
4x = 3 => x = 3/4
log₁₆8 = 3/4.

E.g.11

Solve log_x125 = 3
x³ = 125
Now write down 125 with the base 5.
x³ = 5³
x = 5

E.g.12

Solve log_x9 = 0.5
x^1/2 = 9
Now write down 9 with the base 81.
x^1/2 = 81^1/2
x = 81

Laws of Indices

Indices and logarithms go hand in hand. So, it's really important to understand the rules of indices, in order to deal with logarithms. The following examples may be helpful, when it comes to revising the basic rules of indices:

1. a^x . a^y = a^{x + y}

E.g.
2³ . 2⁴ = 2^{3 + 4} = 2⁷

2. a^x / a^y = a^{x - y}

E.g.
2⁷ / 2⁴ = 2^{7 - 4} = 2³

3. (a^x)^y = a^xy

E.g.
(2³)² = 2^3X2 = 2⁶

Laws of Logarithms

1. log_a(xy) = log_ax + log_ay

Proof:
Let log_a(x) = k and log_a(y) = l
So, a^k = x and a^l = y
By multiplying together, xy = a^k X a^l = a^{k + l}
log_a(xy) = k + l = log_a(x) + log_a(y).

E.g.

Find log_a(4X3).
log_a(4X3) = log_a4 + log_a3.

2. log_a(x/y) = log_ax - log_ay

Proof:
Let log_a(x) = k and log_a(y) = l
So, a^k = x and a^l = y
By dividing, x/y = a^k :- a^l = a^{k - l}
log_a(x/y) = k - l = log_a(x) - log_a(y).

E.g.

Find log_a(5/2).
log_a(5/2) = log_a5 - log_a2.

3. log_a(x)^y = ylog_ax

Proof:
Let log_a(x) = k
a^k = x
(a^k)^y = x^y
a^ky = x^y
log_a(x^y) = ky
log_a(x^y) = ylog_a(x).

E.g.

Find log_a(4)³.
log_a(4)³ = 3log_a4.

Additional Rule 1: log_a(1/x)= -log_ax

Proof:
log_a(1/x) = log_a(1) - log_a(x)
= 0 - log_a(x)
- log_a(x).

E.g.

Express log_a(1/4) in an alternate form.
log_a(1/4) = -log_a4.

Additional Rule 2: log_b(x)= log_ax/log_ab

Proof:
Let log_b(x) = k
b^k = x
Taking log to the base a on both sides,
log_a(b^k) = log_a(x)
k log_a(b) = log_a(x)
k = log_a(x)/log_a(b)
log_b(x) = log_a(x)/log_a(b).

E.g.

Find log₄(8) as a logarithm of the base 2.
log₄8 = log₂8/log₂4
Let x = log₂8 => 2^x = 8 => x = 3
Let y = log₂4 => 2^y = 4 => y = 2
log₄8 = 3/2

Additional Rule 3: log_x(y)= 1/log_yx

Proof:
From the additional rule 2,
log_x(y) = log_y(y)/log_y(x)
= 1/log_y(x).

E.g.

Express log₄(8) in an alternate form.
log₄(8) = 1/log₈4.

Logarithms Problem Solving

E.g.1

Write log₃8 + log₃7 as a single logarithm.
log₃8 + log₃7 = log₃8X7
log₃56.

E.g.2

Write log₃5 + log₃4 - log₃2 as a single logarithm.
log₃5 + log₃4 - log₃2 = log₃(5X4/2)
log₃10.

E.g.3

Simplify log₃81 - log₃9
log₃81 - log₃9 = log₃(81/9)
= log₃9
Let x = log₃9
3^x = 9 = 3²
x = 2
log₃81 - log₃9 = 2.

E.g.4

Simplify 2 log₃9 - log₃27
2 log₃9 - log₃27 = log₃9² - log₃27
= log₃(81/27)
= log₃3
Let x = log₃3
3^x = 3 = 3¹
x = 1
2 log₃9 - log₃27 = 1.

E.g.5

Simplify 3 log₃5 - 2 log₃5
3 log₃5 - 2 log₃5 = log₃5³ - log₃5²
= log₃(125/25)
= log₃5.

E.g.6

Simplify 3 log₆6 - 2 log₆6
3 log₆6 - 2 log₆6 = log₆6³ - log₆6²
= log₆(216/36)
= log₆6
Let x = log₆6
6^x = 6 = 6¹
x = 1
3 log₆6 - 2 log₆6 = 1.

E.g.7

Simplify 3 log₄4 + 1/2 log₄4 - 2 log₄4
3 log₄4 + 1/2 log₄4 - 2 log₄4 = log₄4³ + log₄4^1/2 - log₄4²
= log₄(64X2/16)
= log₄8
Let x = log₄8
4^x = 8
(2²)^x = 2³
2x = 3 => x = 3/2
3 log₄4 + 1/2 log₄4 - 2 log₄4 = 3/2.

E.g.8

Simplify 4 log₁₀10 - (2 log₁₀5 + 2 log₁₀2)
4 log₁₀10 - (2 log₁₀5 + 2 log₁₀2 = log₁₀10⁴ - (log₁₀5² + log₁₀2²)
= log₁₀(10000/25X4)
= log₁₀100
Let x = log₁₀100
10^x = 100
10^x = 10²
x = 2
4 log₁₀10 - (2 log₁₀5 + 2 log₁₀2) = 2.

E.g.9

Write in terms of log_xa, log_xb and log_xc, the simplified term of log_x(a²b / √c).
log_x(a²b / √c) = log_xa² + log_xb - log_x√ c
= 2 log_xa + log_xb - 1/2 log_xc

E.g.10

Write in terms of log_xa and log_xb, the simplified term of log_x(a²b²).
log_x(a²b²) = log_xa² + log_xb²
= 2 log_xa + 2 log_xb
= 2(log_xa + log_xb).

Solving equations involving logarithms

E.g.1

Solve 10^x = 102.
Before finding the value of x, we can estimate it; since 10² = 100, x must be slightly bigger than 2.
10^x = 102 => log₁₀102 = x
From calculator, log₁₀102 = 2.009
So, x = 2.009(3 d.p.).

E.g.2

Solve 10^{2x - 1} = 400.
10^{2x - 1} = 400 => log₁₀400 = 2x - 1
From calculator, log₁₀400 = 2.6
So, 2x - 1 = 2.6
2x = 3.6
x = 1.8

E.g.3

Solve 5^x = 130.
Since 5³ = 125, x must be slightly bigger than 3. Let's solve this by logarithms of different bases.
Method 1 - using log to the base 10
log₁₀5^x = log₁₀130
x log₁₀5 = ₁₀130
x = ₁₀130/₁₀5
= 3.02(2dp)
Method 2 - using log to the base e
log_e5^x = log_e130
x log_e5 = log_e130
x ln(5) = ln(130)
x = ln(130)/ln(5)
= 3.02(2 d.p.)
The answer is almost the same regardless of the log base.

E.g.4

Solve 5^{(2x + 1)} = 3^{(x - 1)} .
log(5^{2x + 1}) = 3^{(x - 1)}
(2x + 1)log 5 = (x - 1)log 3
(2x + 1)/(x - 1) = log 3 / log 5
(2x + 1)/(x - 1) = log 3 / log 5 = 0.6826
2x + 1 = 0.6826x - 0.6826
1.3174x = -1.6826
x = -1.28

E.g.5

Solve 3^2x + 4(3^x) - 12 = 0.
Let y = 3^x => 3^2x = 3^x . 3^x = y²
So, the equation becomes, y² + 4y - 12 = 0
(y + 6)(y - 2) = 0
y = -6 or y = 2
Since, y, 3^x - an exponential function - cannot be negative,
y = 2 => 3^x = 2
log 3^x = log 2
x log 3 = log 2
x = log 2/ log 3
x = 0.63(2 d.p.)

E.g.6

log₃x + 8/log₃x = 6
Let y = log₃x
y + 8/y = 6
y² + 8 = 6y
y² - 6y + 8 = 0
(y - 4)(y - 2)=0
y = 4 or y = 2
log₃x = 4 or log₃x = 2
x = 3⁴ or x = 3²
x = 81 or x = 9

E.g.6

log₅(3 - 2x) = log₂₅(5x² - 13x + 3)
= log₅(5x² - 13x + 3) / log₅25
Since log₅25 = 2,
log₅(5x² - 13x + 3) / log₅25 = log₅(5x² - 13x + 3) / 2
2 log₅(3 - 2x) = log₅(5x² - 13x + 3)
log₅(3 - 2x)² = log₅(5x² - 13x + 3)
log₅(3 - 2x)² - log₅(5x² - 13x + 3) = 0
log₅[(3 - 2x)² / (5x² - 13x + 3)] = 0
Since log(1) = 0 => [(3 - 2x)² / (5x² - 13x + 3)] = 1
9 - 12x + 4x² = 5x² - 13x + 3
x² - x - 6 = 0
(x - 3)(x + 2) = 0
x = 3 or x = -2
Since x = 3 is not valid for log(3 - 2x),
x = -2

Sketching Straight Lines from Curves

Thanks to logarithms, a complex mathematical relationship can be sketched as straight line, after a transformation in the format. In practice, it is tremendously useful and easy to analyse the relationship.

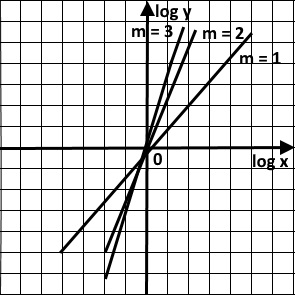
Suppose, the relationship involved is y = xⁿ, where n is a constant.
So, log y = log xⁿ
log y = n log x
This is in the form of y = mx, which is a straight line, as follows:

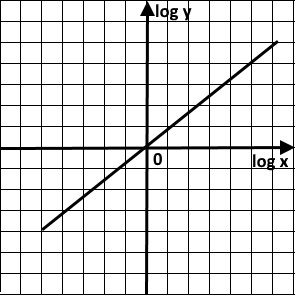
The gradient, m = n

In the same way, we can turn the following curves into straight lines easily by converting the variables into logarithms.
y = x² => log y = 2 log x
y = x³ => log y = 3 log x
y = x⁴ => log y = 4 log x
The gradient of each line is the index number of each function of the corresponding curve. The straight lines are as follows:

In addition, even a complex relationship can be turned into a corresponding logarithm function.

Suppose, y = pxⁿ
log y = log pxⁿ
log y = log p + log xⁿ
log y = log p + n log x
log y = n log x + log p
y = mx + c
The line is as follows:

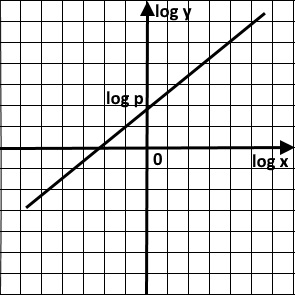
The gradient, m = n; y-intercept = log p

 

Do you want this tutorial with more worked examples? It's available at Amazon: