L'Hospital Rule
Guillaume de l'Hôpital, famously known as L'Hospital, came up with a method to deal with fractions, when they take the indeterminate forms, approaching certain limits.
The indeterminate form can be as follows:
- 0/0 - as in the case of sin(x)/x, when x approaches 0
- ∞ / ∞ - as in the case of ex2 / x2, when x approaches ∞
L'Hospital Rule help us deal with situations of this kind. It is as follows:
L'Hospital Rule
If Limit[f(x)/g(x)] as x approaches a is 0/0 or ∞ / ∞, then Limit[f(x)/g(x)] as x approaches a is [f'(x)/g'(x)].
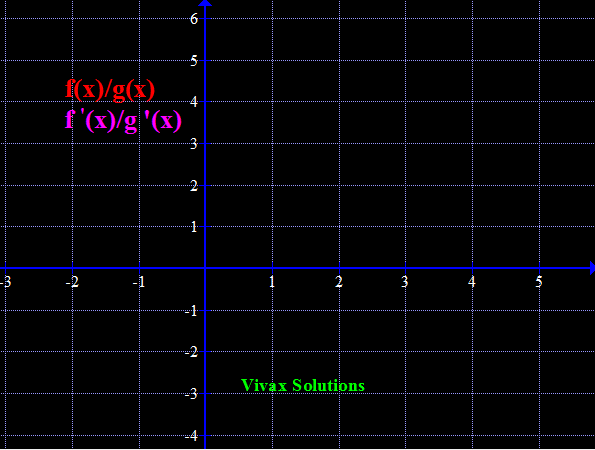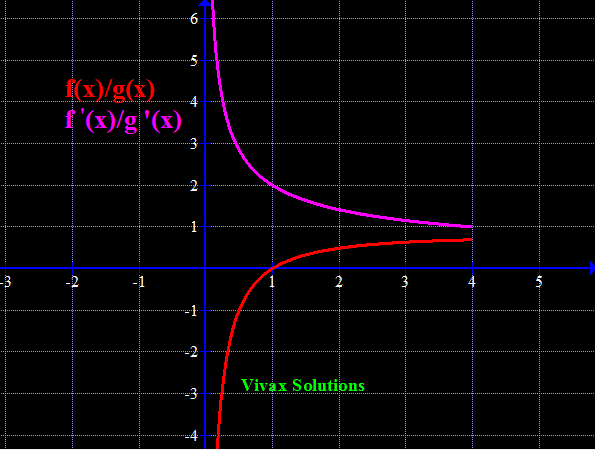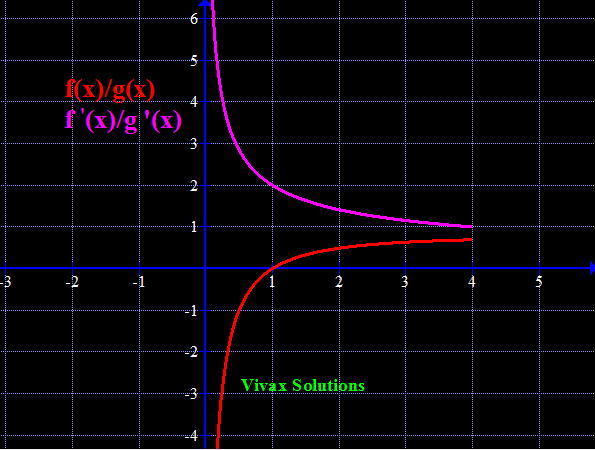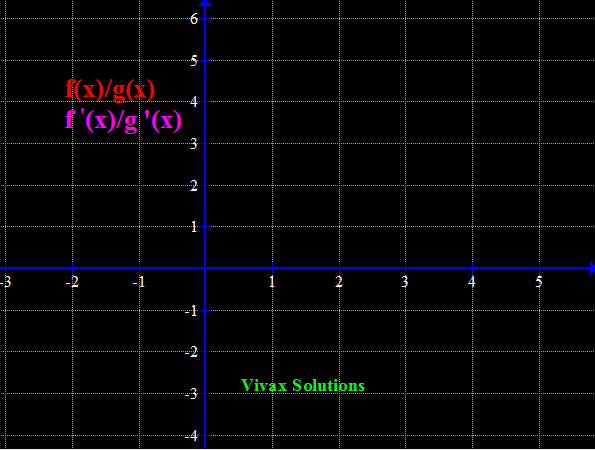
In all the following animations, [f(x)/g(x)] is drawn in red and [f'(x)/g'(x)] in purple.
Please note the convergence pf the two curves / lines to the same point, as the limit approaches.
E.g.1
Find Limit [(4x-3)/(5x-6)] as x approaches ∞.
If x = ∞, then [(4x-3)/(5x-6)] = ∞/∞ - indeterminate
Let's use L'Hospital rule for this:
f'(x)/g'(x) = 4/5 = 0.8, as x approaches ∞
E.g.2
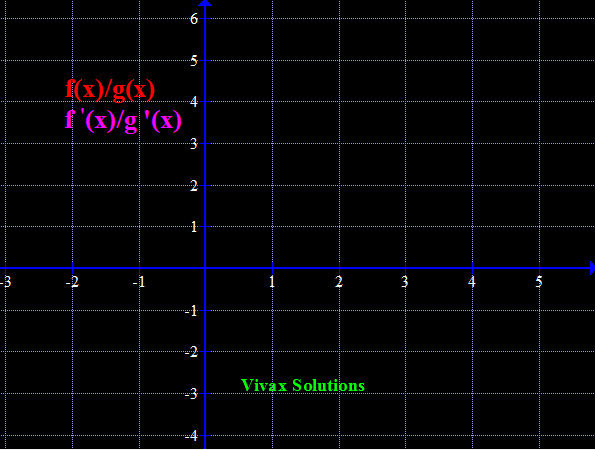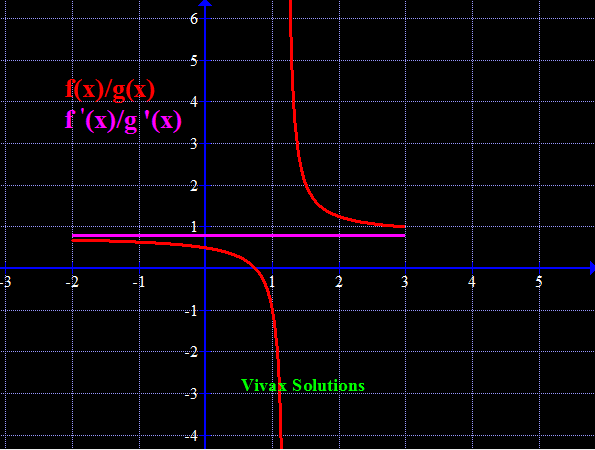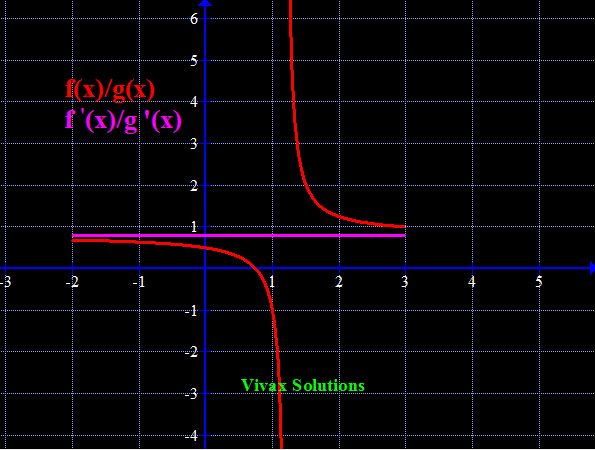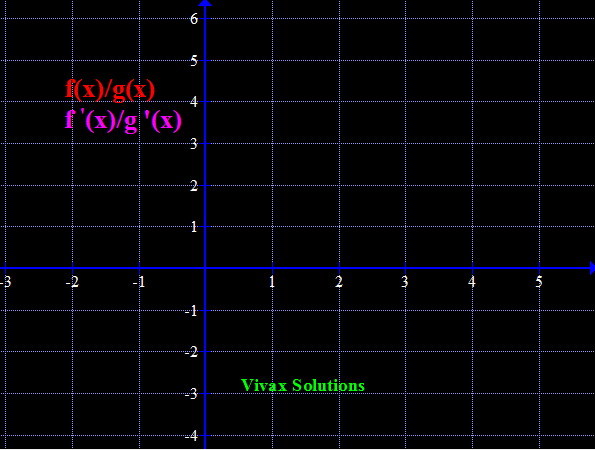
Find Limit [(x-4)/ln(x-3)] as x approaches 4.
If x = 4;, then [(x-4)/ln(x-3)] = 0/0 - indeterminate
Let's use L'Hospital rule for this:
f'(x)/g'(x) = 1/(1/x-3) = 1, as x approaches 4.
E.g.3
Find Limit [ln(x)/√x] as x approaches ∞.
If x = ∞, then [ln(x)/√x] = ∞/∞- indeterminate
Let's use L'Hospital rule for this:
f'(x)/g'(x) = (1/x)/(1/2)x-1/2 = 2/√x = 0, as x approaches ∞.
The behaviour of the curve will be clearer when x is really large.
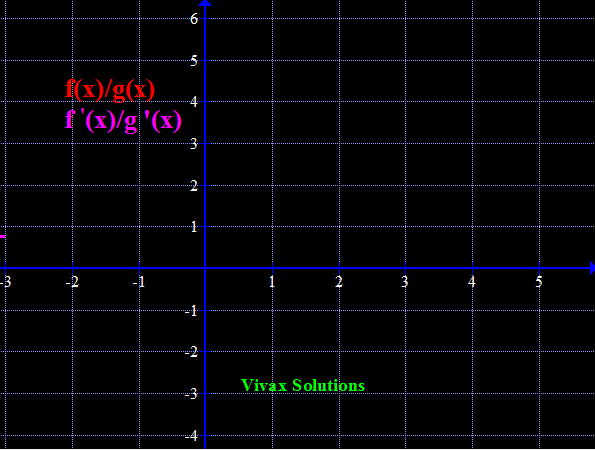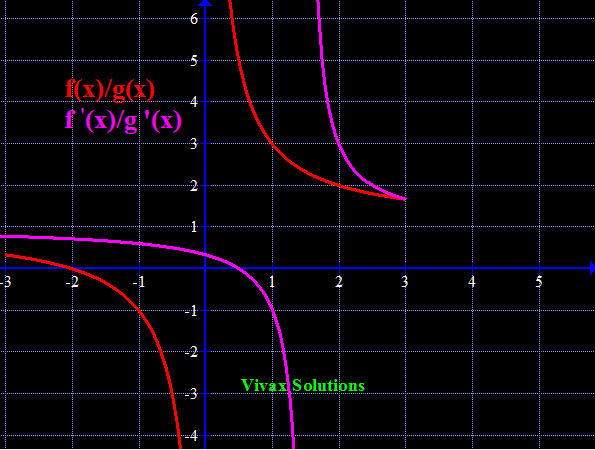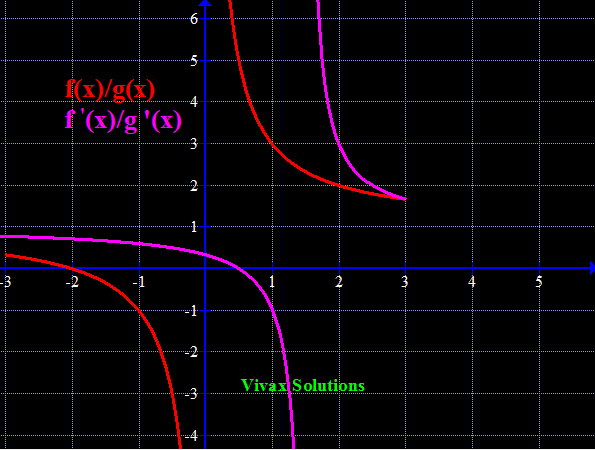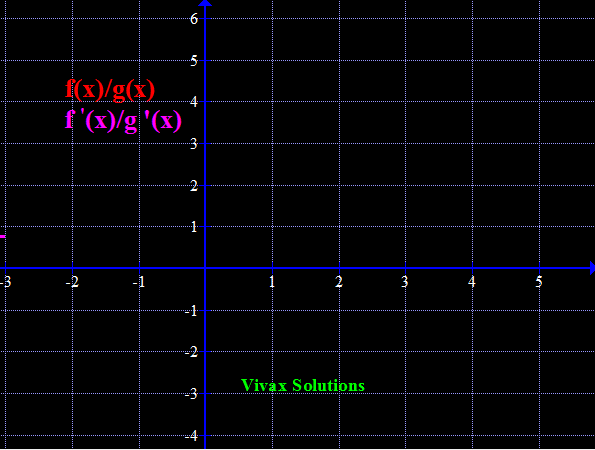
E.g.4
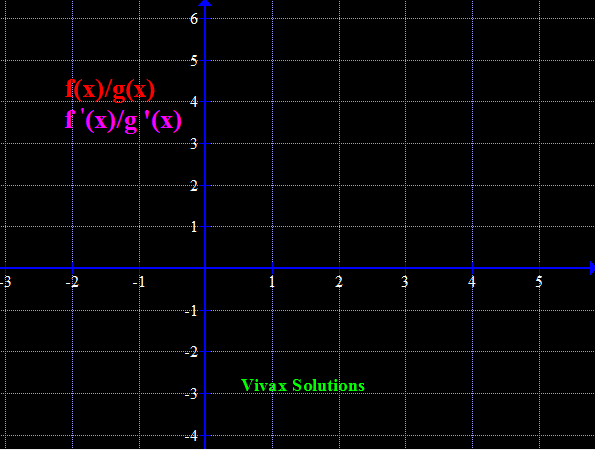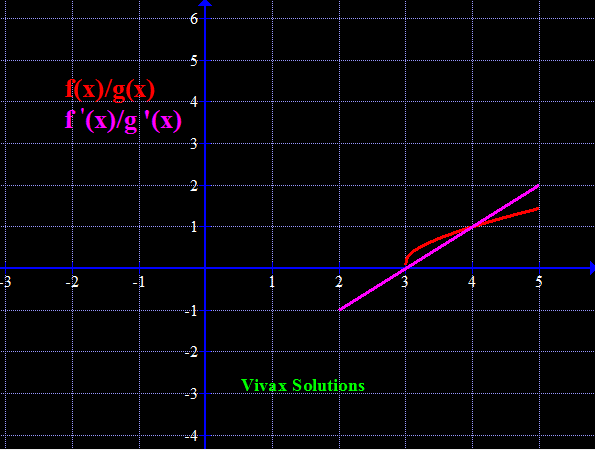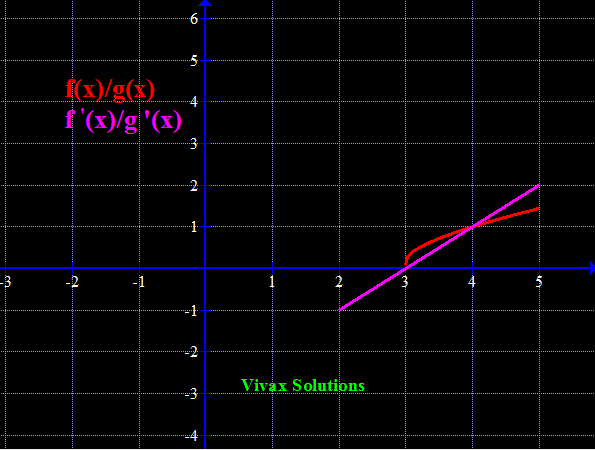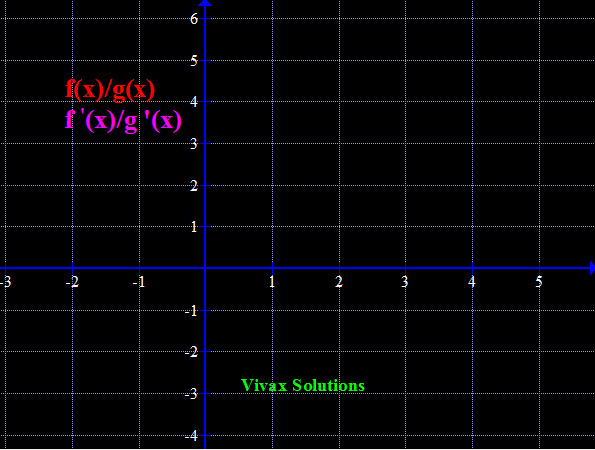
Find Limit [(x2 -x - 6)/(x2 -3x)] as x approaches 3;.
If x = 3, then [(x2 -x - 6)/(x2 -3x)] = 0/0 - indeterminate
Let's use L'Hospital rule for this:
f'(x)/g'(x) = (2x-1)/(2x-3) = 5/3, as x approaches 3.
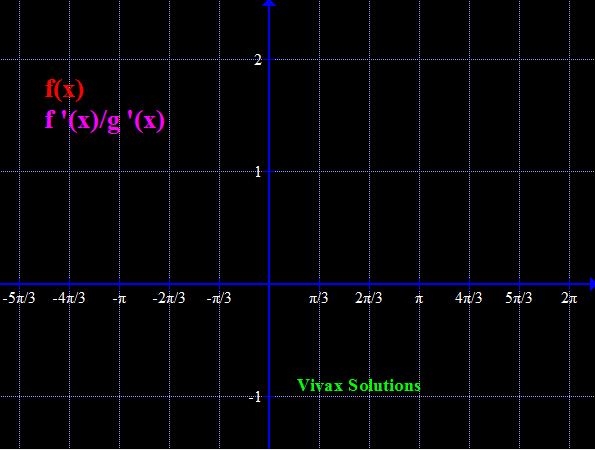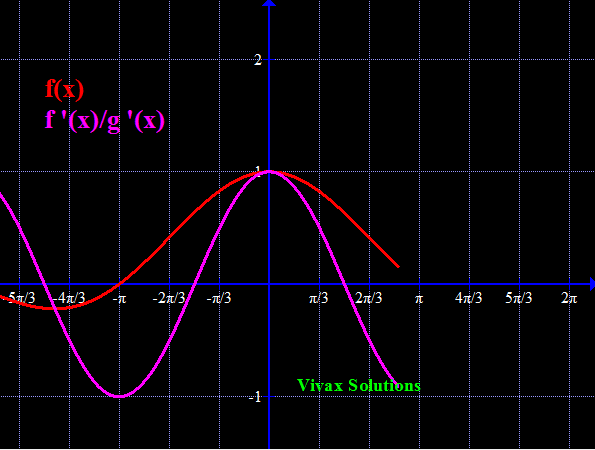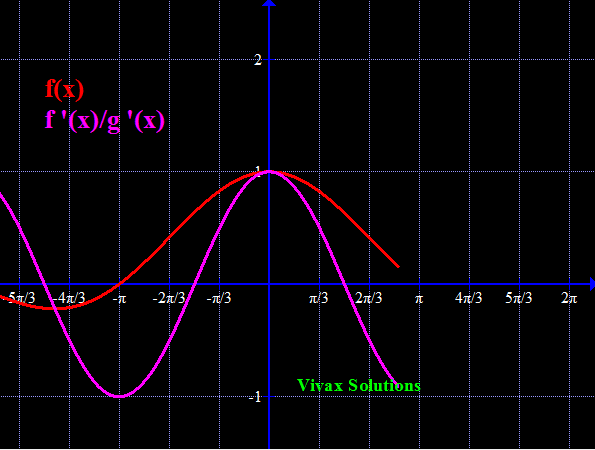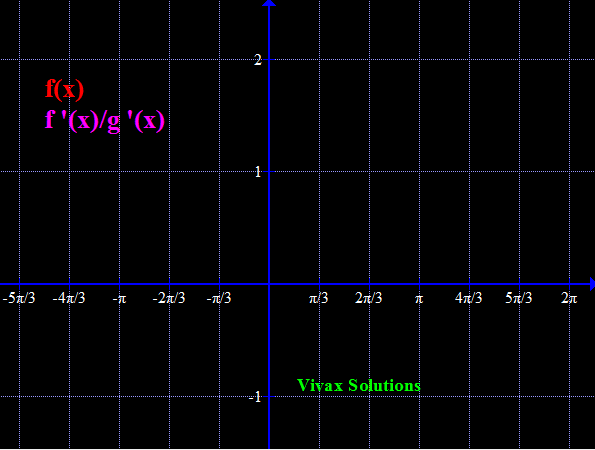
E.g.5
Find Limit sin(x) /x as x approaches 0 and hence sketch y = sin(x)/x.
sin(x) /x when x approaches 0 = sin(0)/0 = 0/0 - indeterminate
Let's use L'Hospital rule for this:
f'(x) = cos(x); g'(x) = 1
So, f'(x)/g'(x) = cos(x)/1
When x approaches 0, f'(x)/g'(x) = 1/1 = 1
Therefore, sin(x)/x, when x approaches 0 = 1.