Cracking the GMAT Code: Free Beginner to Advanced Prep

Dreaming of top business schools? The GMAT can be your gateway, but conquering it requires strategic preparation. This free, comprehensive GMAT prep course empowers you to master the test, from fundamental concepts to advanced strategies. It will guide you through every section, equipping you with the knowledge and skills to achieve your target score. Start following it today and unlock your full GMAT potential!

With this interactive tutorial, you can master every major math topic that comes in the latest GMAT exams. In most topics, you can generate questions at random, work them out and then, check the answers too.

The topics covered are as follows:

Basic Arithmetic

a + b → sum
a - b → difference
a x b → product
a :- b → division

Place Value of a Number

In the above example, there 4-ones, 3-tens, 2-hundreds and 5-thousands.That means, the following takes place in our heads as soon as we look at the number:
5x1000 + 2x100 + 3x10 + 4x1
5000 + 200 + 30 + 4
5234

E.g.1

258
2x100 + 5x10 + 8x1
= 200 + 50 + 8
= 258

E.g.2

5058
5x1000 + 0x100 + 5x10 + 8x1
= 5000 + 0 + 50 + 8
= 5058

E.g.3

Find the sum of 45 + 34, using the place values.
(4+3)tens → 7x10 = 70
(5+4)units → 9x1 = 9
= 70 + 9
= 79

E.g.4

Find the sum of 65 + 36, using the place values.
(5+6)units → 11 → 1ten + 1 unit
Now 10s count goes up by 1
(6+3+1) tens → 10x10 = 100
= 100 + 1
= 101

E.g.5

Find the sum of 85 - 32, using the place values.
(5-2)units → 3x1 = 3
(8-3)tens → 5x10 = 50
= 50 + 3
= 53

Fractions

A part of a whole number is a fraction; the numbers at the top and bottom are called the numerator and denominator respectively.
E.g.
1/2, 1/3, 2/5, 4/7

E.g.
¹²/₇ → 1⁵/₇
²⁷/₅ → 5²/₅

By convention, an improper fraction is usually written as a mixed number.

When writing a fraction, it should be written in the simplest form as follows:
E.g.
¹²/₃₆
Divide both the top and the bottom by 12
¹²/₃₆ → ¹/₃
E.g.
²⁴/₇₅
Divide both the top and the bottom by 3
²⁴/₇₅ → ⁸/₂₅

 

LCM - Lowest Common Multiple

The common multiple of two or more numbers that is the smallest is called the lowest common multiple.
E.g.1
3, 4 → multiples of 3: 3, 6, 9, 12, 15, 18... | multiples of 4: 4, 8, 12, 16, 20
LCM = 12
E.g.2
5, 6 → multiples of 5: 5, 10, 15, 20, 25, 30, 35... | multiples of 6: 12, 18, 24, 30, 36
LCM = 30
E.g.3
2, 3, 4 → multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26... | multiples of 3: 6, 9, 12, 15, 18, 21, 24, 27 | multiples of 4: 4, 8, 12, 16, 20, 24, 28
LCM = 24

 

 

HCF - Highest Common Factor ≡ GCD - Greatest Common Divisor

The common factor of two or more numbers that is the highest is called the highest common factor or greatest common divisor.
E.g.1
12, 15 → factors of 12: 2, 3, 4, 6, 12 | factors of 15: 3, 5, 15
HCF = 3
E.g.2
18, 48 → factors of 18: 2, 3, 6, 18 | factors of 48: 2, 3, 4, 6, 8, 12, 16, 24, 48
HCF = 6
E.g.3
12, 18, 24 → factors of 12: 2, 3, 4, 6, 12 | factors of 18: 2, 3, 6, 9 | factors of 24: 2, 3, 4, 6, 12, 24
HCF = 6

 

 

Prime Numbers

Numbers that can only be divided by itself and 1 are called prime numbers.

E.g. 2,3,5,7,9,11,13,.........................

1 is not a prime number; 2 is the only number that is both prime and even.

 

Prime Factors

When the factors of a number is written in the form of prime factors, they are called prime factors.

E.g. 12 - 1,2,3,4,6 and 12 are factors of 12, but they are all not prime factors

However, when 12 is written in terms of 2X2X3, both 2 and 3 are called prime factors.

In order to find prime factors of a number, keep dividing it with prime numbers, starting with the smallest, until you end up with a prime number.

E.g.

240 :-2 = 120 ⇒ 120 :- 2 = 60 ⇒ 60 :- 2 = 30 ⇒ 30 :-2 = 15 ⇒ 15 :- 3 = 5
240 = 2 X 2 X 2 X 2 X 3 X 5
240 = 2⁴ X 3 X 5

Prime factors can be used to find HCF and LCM of two numbers.

HCF / GCD - Highest Common Factor / Greatest Common Divisor with prime factors

1. Find the prime factors of both numbers first.
2. Then take the common prime factors out.
3. Multiply the lowest power of common prime factors; that gives HCF

E.g.1

Find the HCF of 150 and 120.
150 = 2 X 3 X 5 X 5 = 2 X 3 X 5²
120 = 2 X 2 X 2 X 3 X 5 = 2³ X 3 X 5
The product of lowest power of common factors = 2 X 3 X 5 = 30
So, HCF of 150 and 120 is 30.

E.g.2

Find the HCF of 75 and 120.
75 = 3 X 5 X 5 = 3 X 5²
120 = 2 X 2 X 2 X 3 X 5 = 2³ X 3 X 5
The product of lowest power of common factors = 3 X 5 = 15
So, HCF of 75 and 120 is 15.

You can get questions for practice from this calculator.

 

LCM - Lowest Common Multiple

1. Find the prime factors of both numbers first.
2. Then take the highest power of prime factors of both numbers.
3. Multiply the above prime factors together; that gives LCM

E.g.1

Find the LCM of 150 and 120.
150 = 2 X 3 X 5 X 5 = 2 X 3 X 5²
120 = 2 X 2 X 2 X 3 X 5 = 2³ X 3 X 5
The product of highest power of prime factors = 2³ X 3 X 5² = 600
So, LCM of 150 and 120 is 600.

E.g.2

Find the LCM of 150 and 60.
150 = 2 X 3 X 5 X 5 = 2 X 3 X 5²
60 = 2 X 2 X 3 X 5 = 2² X 3 X 5
The product of highest power of prime factors = 2² X 3 X 5² = 300
So, LCM of 150 and 60 is 300.

You can get questions for practice from this calculator.

Adding and Subtracting Fractions

In order to add or subtract fractions, their denominator must be made the same; it is normally is the LCM

E.g.1
¹⁄₂ + ²⁄₅
Find the Least Common Multiple (LCM) of 2 and 5, which is 10.
Convert the fractions to have a denominator of 10:
¹⁄₂ x (5/5) = ⁵⁄₁₀
²⁄₅ x (2/2) = ⁴⁄₁₀
Add the fractions: ⁵⁄₁₀ + ⁴⁄₁₀ = ⁹⁄₁₀
⁹⁄₁₀

E.g.2
2/₅ + 3/₈
LCM of 5 and 8 = 40
16/₄₀ + 15/₄₀
³¹⁄₄₀

E.g.3
⁵⁄₆ - ¹⁄₃
⁵⁄₆ - ²⁄₆
³⁄₆
¹⁄₂

E.g.4
⁵⁄₆ + ¹⁄₂ + ¹⁄₃
⁵⁄₆ + ³⁄₆ + ²⁄₆
10/6
1⁴⁄₆
1²⁄₃

E.g.5
7⁵⁄₆ + ¹⁄₃ - 1¹⁄₂
Separate Whole Numbers from Fractions:
7 + ⁵⁄₆ + ¹⁄₃ - 1 - ¹⁄₂
Combine Whole Numbers:
6 + ⁵⁄₆ + ¹⁄₃ - ¹⁄₂
Simplify Fractions with the Same Denominator:
6 + ⁵⁄₆ + ²⁄₆ - ³⁄₆
Combine Like Terms:
6 + ⁴⁄₆ = 6⁴⁄₆
6²⁄₃

Multiplying Fractions

Multiply the numerators and denominators separately and simplify, if possible.

E.g.1
²/₃ x ⁴/₅
⁸/₁₅

E.g.2
1²/₃ x ⁴/₅
⁵/₃ x ⁴/₅
²⁰/₁₅
1⁵/₁₅
1¹/₃

E.g.3
1²/₃ x 2⁴/₅
⁵/₃ x ¹⁴/₅
⁷⁰/₁₅
¹⁴/₃
4²/₃

Dividing Fractions

Flip over the second fraction and multiply them together.

E.g.1
³/₅ :- ²/₁₅
³/₅ x ¹⁵/₂
⁴⁵/₁₀
4⁵/₁₀
4¹/₂

E.g.2
2²/₃ :- ⁴/₅
⁸/₃ x ⁵/₄
⁴⁰/₁₂
3⁴/₁₂
3¹/₃

E.g.3
2²/₃ :- 1⁴/₅
⁸/₃ :- ⁹/₅
⁸/₃ x ⁵/₉
⁴⁰/₂₇
1¹³/₂₇

Now, you can practise calculations involving fractions with the following programme; click on the button to get the fractions and a random operation: +, -, x, :-

 

Decimals

Decimals are another way to write fractions, especially those with denominators (the bottom number) that are 10, 100, 1000, and soon. Think of them as tiny slices of a whole, just like fractions!
E.g.
0.2, 0.02, 0.51

Addition and subtraction

E.g.

• 3.2 + 2.6 = 5.8
• 6.4 + 3.8 = 10.2
• 3.2 + 4.35 = 3.20 + 4.35 = 7.55
• 8.6 - 3.2 = 5.4
• 7.4 - 3.6 = 3.8
• 10.2 - 2.54 = 10.20 - 2.54 = 7.66

Multiplication

Multiply the numbers as whole numbers. Then, the sum of decimal places of the two numbers is the number of decimal places in the answer.
E.g.

• 3.2 x 8 = 25.6 → 1 decimal place
• 2.2 x 0.2 = 0.44 → 2 decimal places
• 0.12 x 1.2 = 0.144 → 3 decimal places
• 3.1 x 0.01 = 0.031 → 3 decimal places
• 1.63 x 2. 45 = 3.9935 → 4 decimal places

Division

Make the decimal places of both numbers in the fraction the same, ignore the decimals and just carry out normal integer division.
E.g.

• 32 :- 0.8 = 32.0/0.8 = 320/8 = 40
• 23 :- 0.01 = 23.00/0.01 = 2300/1 = 2300
• 18 :- 0.02 = 18.00/0.02 = 1800/2 = 900
• 4.5 :- 0.05 = 4.50/0.05 = 450/5 = 90
• 120.4 :- 0.2 = 120.4/0.2 = 1204/2 = 602

 

Problem solving with fractions

E.g.1
Tina get ³/₅ of chocolate box that contains 120 chocolates. How many does she get?
'Of' means times or product, in this case,
³/₅ x 120 = 360/5 = 72
Tina gets 72 sweets.

E.g.2
The price of an amplifier has been increased by ¹/₄ of its original value, £240. How much does it cost now?
'Of' means times or product, in this case,
Increase in price = ¹/₄ x 240 = 240/4 = 60
New price = 240 + 60 = £300.00

E.g.3
The price of a bed has been reduced by ²/₅ of its original value, £180. How much does it cost now?
'Of' means times or product, in this case,
Drop in price = ²/₅ x 180 = 360/5 = 72
New price = 180 - 72 = £108.00

 

Percentage - %

When a fraction or a decimal number is multiplied by 100, it becomes a percentage.

E.g.1
Turn ²/₅ into a percentage.
²/₅ x 100 = 200/5 → 40%

E.g.2
Turn 0.25 into a percentage.
0.25 x 100 = 25 → 25%

 

Direct and Inverse Proportion

E.g1
Direct proportion - one thing goes up and so does the related other thing
Five books cost £60. Find the cost of 8 books. How many books can someone buy for £180?
5 books → £60
1 book → ⁶⁰/₅ = £12
8 books → 8 x 12 = £96
------------------------------------
£60 → 5 books
£1 → ⁵/₆₀ = ¹/₁₂ books!
£180 → ¹/₁₂ x 180 = 15 books

E.g2
Inverse proportion - one thing goes up and the related other thing goes down or vice versa
Five men take 60 days to construct a dam. How long will 4 men take to do the same job? If a group of men take 12 days for the same job, how many are there in the group?
5 men → 60 days
1 man → 5 x 60 = 300 days
4 men → 300/4 = 75 days
------------------------------------
60 days → 5 men
1 day → 5 x 60 = 300 men
12 days → 300/12 = 25 men

 

Problem solving with percentages

Sara receives 5% PA for £3000 that she deposits in a bank, every year. Find the interest earned in the first year. Hence, find the total interest after 5 years, if she deposits it for that period.
Interest = 5% of 3000 = ⁵/₁₀₀ x 3000 = 15000/100 = £150
Total interest after 5 years = 5 x 150 = £750.

E.g.2
Adam's salary has been increased by 4% from £40,000. How much is his new salary?
Increase = 4% of 40000 = ⁴/₁₀₀ x 40000 = 160000/100 = £1600

E.g.3
The price of a necklace, increased by 5%, now costs £63. Find the original price.
If it is £105 now, it was £100 before.
£ 105 → £100
£1 → ¹⁰⁰/₁₀₅
£63 → ¹⁰⁰/₁₀₅ x 63 = £60

E.g.4
The price of a laptop, decreased by 6%, now costs £564. Find the original price.
If it is £94 now, it was £100 before.
£ 94 → £100
£1 → ¹⁰⁰/₉₄
£564 → ¹⁰⁰/₉₄ x 564 = £600

 

Directed Numbers

E.g.

-3, +4, -0.5 are called directed numbers, as they carry '+' or '-' before the number; the positive numbers, however, usually do not carry '+' sign.

You can use the above slider to get an idea about how directed numbers work. When the slider moves to the left, you take away the movement from a number and if moved to the right, you add that to a number, as follows:

E.g.
8 - 2 → move the sider to 8, and then move 2 points to the left → answer = 6
-6 - 2 → move the sider to -6, and then move 2 points to the left → answer = -8
-4 + 2 → move the sider to -4, and then move 2 points to the right → answer = -2

When you take away a negative number from a number, the sign becomes '+'.
E.g.
8 - -4 = 8 + 4 = 12
-8 - -4 = -8 + 4 = -4

When you multiply or divide a positive number by a negative number, the answer remains negative.
E.g.
8 :- -2 = -4
8 x -4 = -32

When you multiply or divide a negative number by a negative number, the answer remains positive.
E.g.
-8 :- -2 = 4
-8 x -4 = 32

 

Inequalities

Mathematical relationships involving less than, '<', greater than, '>', less than or equal, '≤' and greater than equal, '≥' are called inequalities.

E.g.
x < 5: x is less than 5 → 4, 3, 2, 1, 0, -1, -2,...
x ≥ 3: x is greater than or equal to 3 → 3, 4, 5, 10, 1000, 1200, ...
-2 < x ≤ 5: x is greater than -2, but less than or equal 5 → -1, 0, 1, 2, 3, 4, 5
5 < x and x ≥ 8: x is less than 5 and x is greater than or equal to 8 → 4, 3, 2, 1, 0, -1, -2... or 8, 9, 10, 11, 12...

 

Index Numbers

A number in the form of a^b is an index number - plural, indices. a is called the base and b is called the power or index.

Laws of Indices

1 a^b x a^c = a^b+c
2 a^b :- a^c = a^b-c
3 (a^b)^c = a^bc

E.g.1
5² x 5² = 5²⁺³ = 5⁵
5⁶ :- 5² = 5^6-4 = 5²
(5²)³ = 5^2x3 = 5⁶

E.g.2
2³ x 4 = 2³ x 2² = 2³⁺² = 2⁵
8 x 16 = 2³ x 2⁴ = 2^{3 + 4} = 2⁷
81 :- 9 = 3⁴ :- 3² = 3^{4 - 2} = 3²

E.g.3
(2x²y)³
2³x⁶y³
8x⁶y³

E.g.4
Simplify (11 ¹/₉)^3₂
(¹⁰⁰/₉)^3/₂
(^10²/_3²)^3/₂
1000/²⁷

E.g.5
Simplify (3 ³/₈)^2/₃
(²⁷/₈)^2/₃
(³³/_2³)^2/₃
9/⁴

 

PEDMAS - parenthesis, exponent, division, multiplication, addition, subtraction

PEDMAS highlights the order of mathematical operations. Please follow the steps below to get it right:

1. Deal with what is inside the parentheses first.
2. Then, check for exponent forms in the expression; if any, deal with it next.
3. Having performed the above steps, starting from left to right, deal with division and multiplication in that order.
4. Then, starting from left to right, deal with addition and subtraction.

E.g.1
2 x (3 + 5) x 4² + 9 :- 3 - 2
= 2 x 8 x 4² + 9 :- 3 - 2
= 2 x 8 x 16 + 3 - 2
= 16 x 16 + 3 - 2
= 256 + 3 - 2
= 256 + 1
= 257

E.g.2
25 :- (1 + 2²) + 3 x 4 - 6
= 25 :- (1 + 4) + 3 x 4 - 6
= 25 :- 5 + 3 x 4 - 6
= 5 + 3 x 4 - 6
= 5 + 12 - 6
= 17 - 6
= 11

E.g.3
58 - (2² + 3²) :- 13 x 4 - 11
= 58 - (4 + 9) :- 13 x 4 - 11
= 58 - 13 :- 13 x 4 - 11
= 58 - 1 x 4 - 11
= 58 - 4 - 11
= 54 - 11
= 43

E.g.4
112 - 4² - 2(3 + 4)² - 6 x 4 + 5
= 112 - 4² -2 x 7² - 6 x 4 + 5
= 112 - 16 -2 x 49 - 6 x 4 + 5
= 112 - 16 - 98 - 24 + 5
= 112 - 16 - 98 - 19
= 96 - 98 - 19
= -2 - 19
= -21

E.g.5
(3 x 5 + 1)² - 24 :- 4 x 3 + 6 - 2
= (15 + 1)² - 24 :- 4 x 3 + 6 - 2
= 16² - 24 :- 4 x 3 + 6 - 2
= 256 - 24 :- 4 x 3 + 6 - 2
= 256 - 6 x 3 + 6 - 2
= 256 - 18 + 6 - 2
Deal with the like terms exactly as in Algebra
= 262 - 20
= 242

When using the following calculator,
If you want, multiplication, "x", enter "*" for it. If you want, exponentiation or power, use "**" for it. For division,":-", use /. Between a number and parenthesis, use "*".
E.g.
2 x 3² → 2*3**2
12 :- 3 → 12/3
2(5 + 4) → 2*(5+4)

If you want more practice material for arithmetic, ranging from fractions to decimals, please follow the link below:
Math Worksheet Generator

Basic Algebra

Algebraic Expressions

E.g

• 2x + 3x = 5x
• 2x + 3y + 6y = 2x + 9y
• 8x + 6y - 2x - y = 6x + 5y
• 2(x + y) + 3x + 2y = 2x + 2y + 3x + 2y = 5x + 4y
• 5 - 2(2x - 3) = 5 - 4x + 6 = 11 - 4x
• 3(4x - y) + 2(5x + 3y) = 12x - 3y + 10x + 6y = 22x + 6y
• (x + y)² = (x + y)(x + y) = x² + xy + xy + y² = x² + 2xy + y²
• (2x - 3y)² = (2x - 3y)(2x - 3y) = 4x² 6xy - 6xy + 9y² = 4x² - 12xy + 9y²
• (x + 2y)² + (x - y)² = x² + 4xy + 4y² + x² - 2xy + y² = 2x² + 2xy + 5y²
• (2x - 3)² - (3x + 2)² = [4x² - 12x + 9] - [9x² + 12x + 4] = 4x² - 12x + 9 - 9x² - 12x - 4 = -5x² - 24x + 5

 

Simple Linear Equations

In this section, you will learn how to solve linear, simultaneous and quadratic equations, along with corresponding problem solving.

 

Simple Equations

 

 

An equation is almost a sort of seesaw: you add something to the left, lose the balance and are forced to do the same to the right; you divide and multiply by something, once again, the same must be done to the other side; if you subtract something, there is no exception. Therefore, solving equation means, getting rid of everything around x by seesaw method.

E.g.1

x + 5 = 8
- 5 => x + 5 -5 = 8 - 5
x = 3

E.g.2

x - 5 = 10
+ 5 => x -5 + 5 = 10 + 5
x = 15

E.g.3

2x = 10
:- 2 => 2x / 2 = 10 /2
x = 5

E.g.4

x / 5 = 2
X 5 => x /5 X 5 = 2 X 5
x = 10

E.g.5

2x - 4 = 10
+ 4 => 2x - 4 + 4 = 10 + 4
2x = 14
:- 2 => 2x / 2 = 14 / 2
x = 7

E.g.6

2x + 4 = 10
- 4 => 2x + 4 - 4 = 10 - 4
2x = 6
:- 2 => 2x / 2 = 6 / 2
x = 3

E.g.7

x/3 + 7 = 10
-7 => x/3 + 7 - 7 = 10 - 7
x/3 = 3
X 3 => x/3 X 3 = 3 X 3
x = 9

E.g.8

(x - 3) / 4 = 3
X 4 => (x-3) /4 X 4 = 3 X 4
(x-3) = 12
+ 3 => x - 3 + 3 = 12 + 3
x = 15

E.g.9

3x + 3 = x + 10
-3 => 3x + 3 -3 =x + 10 - 3
3x = x + 7
- x => 3x - x = x - x + 7
2x = 7
:-2 => 2x / 2 = 7 / 2
x = 3.5

E.g.10

2x - 4 = 5x + 8
+4 => 2x - 4 + 4 = 5x + 8 + 4
2x = 5x + 12
-5x => 2x - 5x = 5x - 5x + 12
-3x = 12
:--3 => -3x/-3 = 12 / -3
x = -4

 

Simple Equation Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the question first, work out the solution and then check with the answer shown below the question.

 

Hard Linear Equations

E.g.1

2(x + 5) = 18
:- 2 => 2(x + 5) :- 2 = 18 :- 2
x + 5 = 9
- 5 => x + 5 - 5 = 9 - 5
x = 4

E.g.2

5(x - 2) = 2(x - 3)
5x - 10 = 2x - 6
+10 => 5x - 10 + 10 = 2x - 6 + 10
5x = 2x + 4
-2x => 5x - 2x = 2x - 2x + 4
3x = 4
:-3 => 3x / 3 = 4 /3
x = 1.3

E.g.3

4(x + 4) + 3(x -3) = 2(x -3) + 12
4x + 16 + 3x - 9 = 2x - 6 + 12
7x + 7 = 2x + 6
- 7 => 7x + 7 - 7 = 2x + 6 - 7
7x = 2x - 1
-2x => 7x - 2x = 2x - 2x -1
5x = -1
:-5 => 5x / 5 = -1 / 5
x = -0.2

E.g.4

(x + 5) / 4 = (x -3) / 2
X 4 => 4 X (x + 5) /4 = 4 X (x- 3) / 2
(x + 5) = 2 (x -3)
x + 5 = 2x - 6
- 5 => x +5 -5 = 2x - 6 - 5
x = 2x - 11
-2x => x - 2x = 2x - 2x -11
-x = -11
-1 X x = 11

E.g.5

3 + 2(x + 5) = 3 - (2x - 1)
3 + 2x + 10 = 3 -2x + 1
13 + 2x = 4 - 2x
-13 => 2x + 13 - 13 = 4 - 2x - 13
2x = -2x - 9
+2x => 2x + 2x = 2x - 2x - 9
4x = -9
:- 4 => 4x / 4 = -9 / 4
x = -2.25

 

Hard Equation Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the question first, work out the solution and then check with the answer shown below the question.

 

Linear Equations: word problems

These are a set of problems that you can solve algebraically. Form the equation from the description and then solve it.

E.g.1

I think of a number, add 7 and the answer is 10. Find the number.
Let the number be x.
x + 7 = 10
-7 => x + 7 -7 = 10 -7
x = 3
The number is 3.

E.g.2

I think of a number, take away 5 and the answer is 10. Find the number.
Let the number be x. x - 5 = 10
+ 5 => x -5 + 5 = 10 + 5
x = 15
The number is 15.

E.g.3

I think of a number, multiply by 3 and the answer is 30. Find the number.
Let the number be x.
3x = 30
:- 3 => 3x / 3= 30 /3
x = 10
The number is 10.

E.g.4

I think of a number, multiply it by 2, take away 4. The answer is 10. Find the number.
Let the number be x. 2x - 4 = 10
+ 4 => 2x - 4 + 4 = 10 + 4
2x = 14
:- 2 => 2x / 2 = 14 / 2
x = 7
The number is 7.

E.g.5

I think of a number, divide by three, add 7. The answer is 10. Find the number.
Let the number be x. x/3 + 7 = 10
-7 => x/3 + 7 - 7 = 10 - 7
x/3 = 3
X 3 => x/3 X 3 = 3 X 3
x = 9
The number is 9.

E.g.6

I think of a number, take away three and then divide by 4. The answer is 3. Find the number.
Let the number be x.
(x - 3) / 4 = 3
X 4 => (x-3) /4 X 4 = 3 X 4
(x-3) = 12
+ 3 => x - 3 + 3 = 12 + 3
x = 15
The number is 15.

E.g.7

I think of a number, multiply by 3, add 3. The answer is the same, if I add 10 to the number. Find the number.
Let the number be x.
3x + 3 = x + 10
-3 => 3x + 3 -3 =x + 10 - 3
3x = x + 7
- x => 3x - x = x - x + 7
2x = 7
:-2 => 2x / 2 = 7 / 2
x = 3.5
The number is 3.5.

E.g.8

I think of a number, multiply by 2, take away 4. The answer is the same if I multiply it by 5 and then add 8. Find the number.
Let the number be x.
2x - 4 = 5x + 8
+4 => 2x - 4 + 4 = 5x + 8 + 4
2x = 5x + 12
-5x => 2x - 5x = 5x - 5x + 12
-3x = 12
:--3 => -3x/-3 = 12 / -3
x = -4
The number is -4.

E.g.9

The width of a rectangle is 2cm less than the length. The perimeter is 20 cm. Find the length and the area.
let the width be x. So, the length = x + 2.
x + x + 2 + x + x + 2 = 20
4x + 4 = 18
-4 => 4x + 4 - 4 = 20 - 4
4x = 16
:-4 => 4x / 4 = 16 / 4
x = 4
Width = 4cm; length = 6cm;
Area = 24 cm².

E.g.10

The sum of two consecutive odd numbers is 52. Find the numbers.
Let the first number be x. Then the next one is x + 2.
x + x + 2 = 52
2x + 2 = 52
-2 => 2x + 2 - 2 = 52 - 2
2x = 50
:-2 => 2x / 2 = 50 / 2
x = 25
The numbers are 25 and 27.

 

Simple Equations - word problems

 

Now, in order to complement what you have just learned, work out the following questions:

1. I think of a number, multiply by 4 and add 5. The answer is 29. Find the number.
2. I think of a number, add 3 and the result is multiplied by 4. The answer is 28. Find the number.
3. I think of a number, add 6 and divide by 3. The answer is 5. Find the number.
4. I think of a number, multiply by 4, and add 6. The result is then multiplied by 5 and the answer is 70. Find the number.
5. Twice a number added to 5 is the same as the number added to 10. Find the number.
6. A number multiplied by 5, add 4 is the same as 6 times the number. Find the number.
7. Three times a number, add nine, divided by 6 is the same as the number itself. Find the number.
8. Twice a number added to 6 is the same as ten subtracted from six times the number. Find the number.
9. The sum of three consecutive numbers is 78. Find the numbers.
10. The sum of three consecutive even numbers is 60. Find the numbers.
11. The sum of the half, the third and the forth of a number is 10 more than the original number. Find the number.
12. The sixth of a number exceeds the eight of the same number by 4. Find the number.
13. Divide £110 among Amy, Basil and Clare in such a way that Amy has £10 more than Basil and Basil has £20 more than Clare.
14. Find a number so that its half exceeds the sum of the fifth and the sixth of the same by 16.
15. A man is twice old as his son is now. Eighteen years ago, he was 5 times as old as his son was then. How old is his son now?
16. The length of a plank of wood is 2cm more than its width. If the length and width were 1cm and 3cm more, the plank would have been a square. Find the length and width of the plank.
17. Anil and Bimal shared £80 between them. When Bimal gives Anil £20, Anil has £12 more than Bimal. How much did then have at the beginning?
18. The sum of two numbers is 112. Find the numbers, if the difference between them is 48.
19. Find two numbers with a difference and a mean, 8 each.
20. The longest side of an isosceles triangle is 4cm more than the twice of each other side. Find the length of the longest side, if the perimeter is 44cm.

 

Simple Equations - answers

 

Move the mouse over, just below this, to see the answers:

1. 6
2. 4
3. 9
4. 2
5. 5
6. 4
7. 3
8. 4
9. 25, 26, 27
10. 18, 20, 22
11. 120
12. 96
13. 50, 40, 20
14. 120
15. 24
16. 6, 4
17. 26, 54
18. 80, 32
19. 12, 4
20. 24

 

Straight Line Graphs

The equation of a straight line takes the form of y = mx + c, where m and c are the gradient and the y-intercept of the line respectively. Both the gradient and y-intercept can be positive, zero or negative.

 

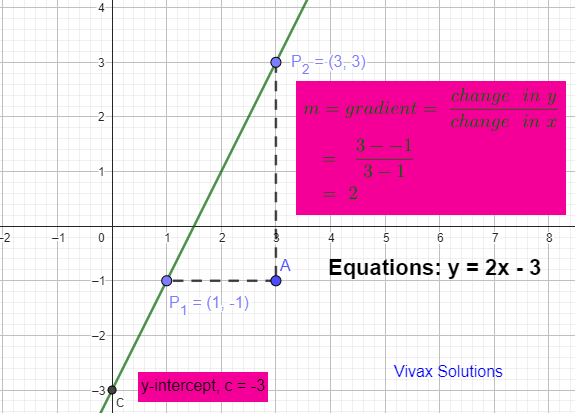
E.g.1
The gradient of a straight line is 5 and it passes through the point, (2, 5). Find its equation.
m = 5 | x = 2 | y = 5
y = mx + c
5 = 5(2) + c
5 = 10 + c
c = -5
y = 5x - 5

E.g.2
The gradient of a straight line is -3 and it passes through the point, (3, 6). Find its equation.
m = -3 | x = 3 | y = 6
y = mx + c
6 = -3(3) + c
6 = -9 + c
c = 15
y = -3x + 15

E.g.3
The gradient of a straight line is 3 and it passes through the point, (4, 12). Find its equation.
m = 3 | x = 4 | y = 12
y = mx + c
12 = 3(4) + c
12 = 12 + c
c = 0
y = 3x

E.g.4
The equation of a straight line is y = 2x - 5. Find the equation of a parallel line that passes through (5, 7).
Since the lines are parallel, they have the same gradient. For the second line,
m = 2 | x = 5 | y = 7
y = mx + c
7 = 2(5) + c
7 = 10 + c
c = -3
y = 2x - 3

E.g.5
The equation of a straight line is y = 4x - 3. Find the equation of a perpendicular line that passes through (4, 5).
Since the lines are perpendicular to each other, the gradient of the second line is -1/4 - negative reciprocal. For the second line,
m = -1/4 | x = 4 | y = 5
y = mx + c
5 = -1/4(4) + c
5 = -1 + c
c = 6
y = -(¹/₄)x + 6

E.g.6
The equation of a straight line is 2y - 3x = 8. Find the equation of a perpendicular line that passes through (3, 5).
2y - 3x = 8
y = ³/₂x + 4
Since the lines are perpendicular to each other, the gradient of the second line is -²/₃ - negative reciprocal. For the second line,
m = -²/₃| x = 3 | y = 5
y = mx + c
5 = -2/3(3) + c
5 = -2 + c
c = 7
y = -(²/₃)x + 7

E.g.7
The coordinates of two points on a straight line are (1, 3) and (4, 9) respectively. Find its equation.
m = ^{9 - 3}/_4-1
m = ⁶/₃ = 2
m = 2 | x = 1 | y = 3 - coordinates of any point can be used here.
y = mx + c
3 = 2(1) + c
3 = 2 + c
c = 1
y = 3x + 1

 

The following simulator can be used to generate a random point and a line that goes through it. You can find the equation of the line by taking into account its gradient and the coordinates of the point in question. Then, you can chcek the answer. You can draw different lines at random for practice.

 

 

Simultaneous Equations

Equations with two unknowns are called simultaneous equations. In order to solve them, they must be boiled down to a single equation, a linear one, first, and then solve it. Here are some methods and worked examples for you to follow them.

Elimination Method

In this method, we must get rid of one variable in order to find the other.

E.g.1

x + y = 6 1
x - y = 2 2
If we add the two equations, we can remove y.
1 + 2 => 2x = 8
x = 4
Sub in 1 => 4 + y = 6
y = 2
Solutions are x = 4 and y = 2.

E.g.2

2x + y = 6 1
3x - 2y = 2 1
To remove y, multiply the first equation by 2 and then add the two equations together.
1 X 2 => 4x + 2y = 123
2 + 1 => 7x = 14
x = 2
Sub in 1
4 + y = 6
y = 2
The solutions are x = 2 and y = 2.

E.g.3

2x + 3y = 1 1
3x - 2y = 8 2
In this case, to eliminate y, the first equation must be multiplied by 2 and the second equation must be multiplied by 3.
1 X 2 => 4x + 6y = 2 3
2 X 3 => 9x - 6y = 24 4
3 + 4 => 13x = 26
x =2
Sub in 1=> 4 + 3y = 1
-4 => 3y = -3
y = -1
The solutions are x = 2 and y = -1.

Substitution Method

We get y in terms of x or vice versa from one equation, and put that in the other.

E.g.1

x + y = 6 1
x - y = 2 2
From 1 => x = (6 - y)
Sub this in 2 => 6 - y - y = 2
6 - 2y = 2
-6 => -2y = -4
:--2 => y = 2
Sub in 1 => x + 2 = 6
x = 4
Solutions are x = 4 and y = 2.

E.g.2

2x + y = 6 1
3x - 2y = 2 2
From 1 => y = (6 - 2x)
Sub this in 2 => 3x - 2(6 - 2x) = 2
3x - 12 + 4x = 2
7x - 12 = 2
+ 12 => 7x = 14
x = 2
Sub in 1 => 4 + y = 6
-4 => y = 2
The solutions are x = 2 and y = 2.

E.g.3

2x + 3y = 1 1
3x - 2y = 8 2
From 1 - 3y => 2x = (1 - 3y)
x = (1 - 3y)/2
Sub in 2 => 3(1 - 3y)/2 - 2y = 8
X 2 => 3(1 - 3y) - 4y = 16
3 - 9y - 4y = 16
3 - 13y = 16
-3 => -13y = 13
y = -1
Sub in 1 => 2x - 3 = 1
+ 3 => 2x = 4
x = 2
The solutions are x = 2 and y = -1.

Graphical Method

In this method, two straight lines are drawn for each equation. Then the point where the two lines intersect at is noted. The coordinates of this point are the solutions of the equations.

E.g.1

2x + y = 8 1
y -x = 1 2
1 => y = 8 - 2x
2 => y = x + 1

x	y = 8 - 2x
0	8
-1	10
2	4

x	y = x + 1
0	1
-1	0
2	3

Rearrange the two equations in the form of y = mx + c and draw two lines for them on the same grid.

 

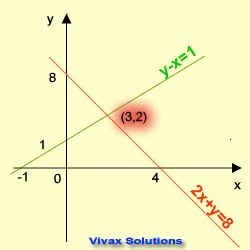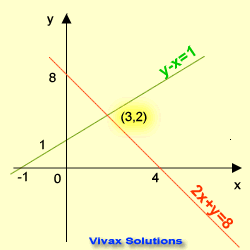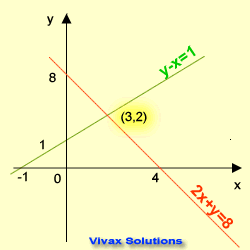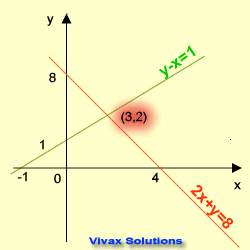
The coordinates of the point of intersection are x = 3 and y = 2.
So, the solutions are x = 3 and y = 2.

 

Simultaneous Equations Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the questions first, work out the solution and then check with the answer shown below the question.

 

Simultaneous Equations - word problems

Equations that must be solved at the same time are simultaneous equations.

E.g.1

The sum of two numbers is 6 and the difference is 2. Find the numbers.
Let the numbers be x and y.
x + y = 6 1
x - y = 2 2
1 + 2 => 2x = 8
x = 4
Sub in 1=> 4 + y = 6
y = 2
The numbers are x = 4 and y = 2.

E.g.2

The sum of two books and a pencil is £6.00. The difference of cost between 3 books and 2 pencils is £2.00. Find the cost of a book and a pencil.
Let the cost of a book be x and that of a pencil be y.
2x + y = 6 1
3x - 2y = 2 2
1 X 2 => 4x + 2y = 123
2 + 3 => 7x = 14
x = 2
Sub in 1
4 + y = 6
y = 2
The cost of a book and a pencil is £2.00 each.

E.g.3

If I double a number and add three times a second number, the answer is 1. If I multiply the first number by 3 and take away twice the second number, the answer is 8. Find the numbers.
Let the numbers be x and y.
2x + 3y = 1 1
3x - 2y = 8 2
From 1 - 3y => 2x = (1 - 3y)
x = (1 - 3y)/2
Sub in 2 => 3(1 - 3y)/2 - 2y = 8
X 2 => 3(1 - 3y) - 4y = 16
3 - 9y - 4y = 16
3 - 13y = 16
-3 => -13y = 13
y = -1
Sub in 1 => 2x - 3 = 1
+ 3 => 2x = 4
x = 2
The numbers are x = 2 and y = -1.

E.g.4

The sum of twice the cost of a box biscuits and the cost of a box chocolates is £8.00. The difference between the cost of box of chocolates and the box of biscuits is £1.00. Find the cost of each.
Let the cost of the box chocolates and the box of biscuits be y and x respectively.
2x + y = 8 1
y -x = 1 2
1 => y = 8 - 2x
Sub in 2 => y = 8 - 2x - x = 1
8 - 3x = 1
-8 => -3x = -9
:- -3 => x = 3
Sub in 1 => 6 + y = 8
-6 => y = 2
The cost of box of chocolates =£2.00 and that of biscuits = £3.00.

Solving Simultaneous Equations - fully interactive

The following applet help you solve simultaneous equations instantly. Just type in the two equations into the text boxes, exactly in the form shown, and then press enter. You may move the grid to see the point of intersection of the two lines.

 

 

Simultaneous Word Problems for Practice

Now, in order to complement what you have just learnt, work out the following questions:

1. The sum of two numbers is 18. The difference is 4. Find the numbers.
2. A straight line passes through (3 , -4) and (5 , 8). Find the equation of the line.
3. The cost of 3 DVD's and 4 CD's is £62.00. The cost of 4 DVD's and 3 CD's is £64.00. Find the cost of each.
4. A diver swims downstream a distance of 40 miles in two hours. If he swims upstream, he can only move 16 miles during the same time. Find his swimming speed and the speed of the river.
5. Half the difference between two numbers is 8. The average of the numbers is 12. Find the numbers.
6. Nicole has 23 notes of £20 and £5 in her hand bag. The amount of money she has in the bag is £340.00. Find the number of notes of each type.
7. There are two angles on a straight line. One angle is 15 more than twice the other. Find the size of each angle.
8. The sum of ages of an uncle and his nephew two years ago was 40. In two years time from now, the age of the uncle will be three times that of his nephew by then. Find their ages in 7 years time.
9. The curve, px² + qx, passes through (3,6) and (1,-2). Find the values of p and q.
10. The numerator of a fraction is 3 smaller than its denominator. If both the numerator and denominator are increased by by 1, the fraction is 5/8. Find the original fraction.
11. A car covers a distance of 220 miles at 3o mph and 20 mph respectively. Find the time taken for each part of the journey.
12. The curve, px² + qx + r, passes through (0,5) and (2,5) and (3,11). Find the values of p, q and r.

 

Answers

Move the mouse over, just below this, to see the answers:

1. 11,7
2. y = 6x - 22
3. 10,8
4. 14,6
5. 20,4
6. 15,8
7. 125, 55
8. 34, 10
9. 2, -4
10. 4/7
11. 6, 2
12. 2, -4, 5

 

Factorisation

The following examples show how to factorize algebraic expressions.

The process of taking common factors out in an algebraic expression is called factorising

E.g.1

2x + 8
2(x + 4)

E.g.2

2x + 8y
2(x + 4y)

E.g.3

4x² + 6x
2x(2x + 3)

E.g.4

ax²p - 2ax³r
ax²(p - 2xr)

In this method, we pair up the terms and then factorize twice as follows:
x² + 6x + 2x + 12
x² + 6x + 6x + 12
First factorizing:
x(x + 6) + 2(x + 6)
Second factorizing:
(x + 6)(x + 2)

E.g.1

2ax + 6ay + bx + 3by
2a(x + 3y) + b(x + 3y)
(x + 3y)(2a + b)

E.g.2

xk - xl - yk + yl
x(k - l) - y(k - l)
(k - l)(x - y)

E.g.3

x² - 6x + 4x - 24
x(x - 6) + 4(x - 6)
(x - 6)(x + 4)

E.g.3

x² - 3x - 2x + 6
x(x - 3) - 2(x - 3)
(x - 3)(x - 2)

Factorizing Quadratic Expressions - easier

An expression with the highest term of x being a squared one, is called a quadratic expression.

E.g.1

x² + 6x + 8
Think of two factors of 8 that add up to 6 - 4 and 2.
Now, split up the middle term into 4x and 2x
x² + 4x + 2x + 8
Now, factorize in pairs
x² + 4x + 2x + 8
x(x + 4) + 2(x + 4)
(x + 4)(x + 2)

E.g.2

x² - 6x + 8
Think of two factors of 8 that add up to -6 - -4 and -2.
Now, split up the middle term into -4x and -2x
x² - 4x - 2x + 8
Now, factorize in pairs
x² - 4x - 2x + 8
x(x - 4) - 2(x - 4)
(x - 4)(x - 2)

E.g.3

x² + 6x - 16
Think of two factors of -16 that add up to 6 - 8 and -2.
Now, split up the middle term into 8x and -2x
x² + 8x - 2x - 16
Now, factorize in pairs
x² + 8x - 2x - 16
x(x + 8) - 2(x + 8)
(x + 8)(x - 2)

Factorizing Quadratic Expressions - harder

E.g.1

2x² + 13x + 6
Multiply 2 and 3 first - 2 x 6 = 12.
Think of two factors of 12 that add up to 13 - 12 and 1.
Now, split up the middle term into 12x and x
2x² + 12x + x + 6
Now, factorize in pairs
2x² + 12x + x + 6
2x(x + 6) + 1(x + 6)
(x + 6)(2x + 1)

E.g.2

3x² - 11x + 6
Multiply 3 and 6 first - 3 x 6 = 18.
Think of two factors of 18 that add up to -11 - -9 and -2.
Now, split up the middle term into -9x and -2x
3x² - 9x - 2x + 6
Now, factorize in pairs
3x² - 9x - 2x + 6
3x(x - 3) - 2(x - 3)
(x - 3)(3x - 2)

E.g.3

4x² - 8x - 5
Multiply 4 and 5 first - 4 x 5 = -20.
Think of two factors of 20 that add up to -8 - -10 and 2.
Now, split up the middle term into -10x and 2x
4x² - 10x + 2x - 5
Now, factorize in pairs
4x² - 10x + 2x - 5
2x(2x - 5) + 1(2x - 5)
(2x - 5)(2x + 1)

Factorizing Difference of Squares

x² - y² = (x + y)(x - y)

E.g.1

x² - 9
x² - 3²
(x + 3)(x - 3)

E.g.2

4x² - 9y²
(2x)² - (3y)²
(2x + 3y)(2x - 3y)

E.g.3

x² - 9/4
x² - (3/2)²
(x + 3/2)(x - 3/2)

E.g.4

x³ - 9x/4
x[x² - 9/4]
x[x² - (3/2)²]
x[(x + 3/2)(x - 3/2)]
x(x +3/2)(x - 3/2)

E.g.4

Find 101² - 99²
(101 - 99)(101 + 99)
2 x 200
400

Now, please practise the following:

1. 3x² - 12x
2. x² - 12x + 20
3. 2x² - 9x -5
4. x² - 25/49
5. x³ - 36x/81
6. x³ - x² + 2x - 2
7. x³ - y² - x² + xy²
8. 5x³ + 5x² - x - 1
9. ax + bx + ay + by - cx - cy
10. 12x² - 8x³ + 9 - 6x

Challenge

The sum of the two factors of x/y - y/x is x/y + y/x . Find the two factors.

 

Factorable Expression Generator

With this simple programme, you can generate questions at random, along with answers in the form of factors - unlimited number of questions. Generate the questions first, work out the solution and then check with the answer shown below the question.

Quadratic Equations

An equation in the form of ax² + bx + c = 0 is called a quadratic equation.

E.g.

• x² + 6x + 8 = 0
• 2x² - 5x + 6 = 0
• x² - 6 = 0
• x² - 6x = 0

A quadratic equation has two solutions; that means there are two values for x that satisfy the equation. There are four different ways to solve a quadratic equation:

1. Factorizing Method
2. Formula Method
3. Graphical Method
4. Completing the Square Method

Factorizing

E.g.1
x² + 8x = 0
x(x + 8) = 0
x = 0 or (x + 8) = 0
x = 0 or x = -8

E.g.2

x²= 6x
x² - 6x = 0
x(x - 6) = 0
x = 0 or (x - 6) = 0
x = 0 or x = 6

E.g.3

x² + 6x + 8 = 0
x² + 4x + 2x + 8 = 0
x(x + 4) + 2(x + 4) = 0
(x + 4)(x + 2) = 0
(x + 4) = 0 or (x + 2) = 0
x = -4 or x = -2

E.g.4

x² - 6x + 8 = 0
x² - 4x - 2x + 8 = 0
x(x - 4) - 2(x - 4) = 0
(x - 4) = 0 or (x - 2) = 0
x = 4 or x = 2<

E.g.5

x² + 6x - 16 = 0
x² + 8x - 2x - 16 = 0
x(x + 8) - 2(x + 8) = 0
(x + 8) = 0 or (x - 2) = 0
x = -8 or x = 2

E.g.6

2x² + 13x + 6 = 0
2x² + 12x + x + 6 = 0
2x(x + 6) + 1(x + 6) = 0
(x + 6) = 0 or (2x + 1) = 0
x = -6 or 2x = -1
x = -6 or x = -1/2

E.g.7

x² - 9/4 = 0
(x + 3/2)(x - 3/2) = 0
x + 3/2 = 0 or x - 3/2 = 0
x = -3/2 or x = 3/2

Formula Method

If ax² + bx + c = 0, then
x = [-b ±√(b² - 4ac) ]/ 2a

E.g.1

x² - 6x + 8 = 0
a = 1; b = -6; c = 8
x = -(-6) ±√((-6)² - 4(1)(8)) / 2(1)
x = 6 ±√(36 - 32) / 2
x = 6 ±√(4) / 2
x = (6 ± 2 )/ 2
x = 4 or x = 2

E.g.1

2x² - 5x + 3 = 0
a = 2; b = -5; c = 3
x = -(-5) ±√((-5)² - 4(2)(3)) / 2(2)
x = 5 ±√(25 - 24) / 4
x = 5 ±√(1) / 4
x = (6 ± 1 )/ 4
x = 1.5 or x = 1

 

Graphical Method

In this method, a graph is plotted for a quadratic function. The graph takes the typical shape, known as parabola.

E.g. Solve x² + 5x - 7 = 0

First of all, make a table for both x and y of the function.

x	y
-2	-13
-1	-11
0	-7
1	-1
2	7
3	17

 

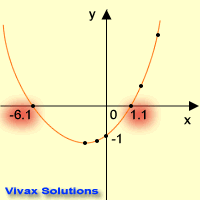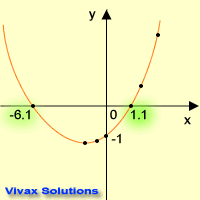
Now, plot a graph of y against x. Note the points at which the curve the crosses the x-axis. They are the solutions of the quadratic function. The solutions are:
x = 1.1 or x = -6.1

The following animation is interactive: it shows how to solve a quadratic equation by a graph; by clicking on the button, you can generate a random equation and its solutions appear at the same time. If there are no solutions - the graph being above the x-axis - instead of solutions, the word, undefined, appears in those places.

 

 

Completing the Square Method

x² + 4x - 5 = 0
Let (x + a)² + b = x² + 4x - 5
x² + 2ax + a² + b = x² + 4x - 5
Now, make the coefficients of x and the constant equal.
x => 2a = 4
a =2
a² + b = -5
4 + b = -5
b = -9
(x + 2)² - 9 = 0
(x +2)² = 9
(x + 2) = ±3
x = -2 ±3
x = 1 or -5

 

Now, in order to complement what you have just learnt, work out the following questions:

Click the button to get the quadratic equations; solve them by all four methods to master the techniques.

Quadratic Equation Generator

 

Simultaneous Quadratic Equations

These equations are simultaneous as there are two unknowns in them; since one of the unknown is in quadratic form, they are quadratic too. Therefore, these equations have two sets of solutions, one for each unknown.

E.g.1

The equation of a circle is x² + y² = 45. It intersects with, y = 2x, at two points. Find the coordinates of the points of intersection.
x² + y² = 45 1
y = 2x 2
Sub y in 1 => x² + 4x² = 45
5x² = 45
:- 5 => x² = 9
x = ± 3
Sub in 2 => y = ±6
Solutions: (3,6); (-3,-6)

E.g.2

The equation of a circle is x² + y² = 25. It intersects with the line, x + y = 7, at two points. Find the coordinates of the points of intersection.
x² + y² = 25 1
x + y = 7 2
y = (7-x)
Sub y in 1 => x² + (7-x)² = 25
x² 49 - 14x + x² = 25
2x² - 14x + 24 = 0
x² - 7x + 12 = 0
(x - 4)(x - 3) = 0
x = 4 or x = 3
Sub in 2
y = 3 or y =4
Solutions: (4,3); (3,4)

 

Simultaneous Quadratic Equation Generator

With this simple programme, you can generate questions at random, along with answers - unlimited number of questions. Generate the questions first, work out the solution and then check with the answer shown below the question. If you don't see the solutions, please click the refresh button on the applet once.

 

Quadratic Equations - word problems

You will get an amazing set of worked examples here involving quadratic equations. In addition, there are lots of questions for you to practise in order to complement your experience that you get from these examples.

E.g.1

The sum of two numbers is 27 and their product is 50. Find the numbers.
Let one number be x. Then the other number is 50/x.
x + 50/x = 27
X x => x² + 50 = 27x
- 27x => x² - 27x + 50 = 0
(x -25)(x -2) = 0
(x -25) = 0 or (x -2) = 0
x = 25 or x = 2.

E.g.2

The length of a rectangle is 5 cm more than its width and the area is 50cm². Find the length, width and the perimeter.
Let the width be x. Then the length = x + 5.
x(x + 5) = 50
x² + 5x = 50
-50 => x² + 5x - 50 = 0
(x + 10)(x -5) =0
(x + 10) = 0 or (x -5) =0
x = -10 or x = 5 - x = -10 is impossible to be a width
Width = 5cm; so, the length = 10cm.
Perimeter = 30cm.

E.g.3

The three sides of a right-angled triangle are x, x+1 and 5. Find x and the area, if the longest side is 5.
The hypotenuse = 5
x² + (x+1)² = 5² (Pythagoras' Theorem)
x² + x² + 2x + 1 = 25
-25 => x² + x² + 2x - 24 = 0
2x² + 2x - 24 = 0
x² + x - 12 = 0
(x - 3)(x + 4) = 0
(x + 4) = 0 or (x - 3) = 0
x = -4 or x = 3
x = 3;
Area = 1/2 x 3 x 4 = 6cm²

E.g.4

The product of two numbers is 24 and the mean is 5. Find the numbers.
Let one number = x; then the other = 24/x
(x + 24/x)/2 = 5
X 2 => x + 24/x = 10
X x => x² + 24 = 10x
- 10x => x² + -10x + 24 = 0
(x - 6)(x -4) = 0
(x - 6) = 0 or (x -4) = 0
x = 6 or x =4
The numbers are 6 or 4.

E.g.5

The sum of numbers is 9. The squares of the numbers is 41. Find the numbers.
These are quadratic simultaneous equations.
let the numbers be x and y.
x + y = 9
x² + y² = 41
From the first equation, y = (9-x)
Now substitute this in the second equation.
x² + (9-x)² = 41
x² + 81 - 18x + x² = 41
2x² - 16x + 81 = 41
2x² - 16x + 40 = 0
x² - 8x + 20 = 0
(x - 5)(x -4) =0
(x - 5) = 0 or (x -4) =0
x = 5 or x = 4
Substitute in the first equation, y = 5 or 4
The numbers are 5 and 4.

 

 

Now, in order to complement what you have just learned, work out the following questions:

Questions

1. The sum of squares of two consecutive even numbers is 244. Find the numbers.
2. The base length of a triangle is 2cm more than its height. The area is 24cm². Find the length of hypotenuse and the perimeter of the triangle.
3. The length of a square is increased by a 5^th so that its new area is 44cm² more than the original value. Find the difference in perimeter of two shapes.
4. The length and width of a rectangular garden are 150m and 120m. A foot path of regular width is added to the boundary of the garden and the total area of the garden becomes 2800m² more than its original area. Find the width of the footpath.
5. Adam is about to embark on a journey on a narrow country lane that covers 32km and decides to go at x km/h. On second thoughts, he calculates that if he increases the speed by 4km/h, his journey time can be cut down by 4 hrs. Find x.
6. The reciprocal of the sum of reciprocals of two numbers is 6. The sum of numbers is 25. Find the numbers.
7. The speed of an ant is (2t + 10) and after travelling for t minutes, it covers a distance of 12m. Find t.
8. Two chords and a diameter form a triangle inside a circle. The radius is 5cm and one chord is 2cm longer than the other one. Find the perimeter and the area of the triangle.
9. The sum of a number and it reciprocal is 26/5. Find the number.
10. The product of two numbers is 20. The sum of squares is 41. Find the numbers.
11. The dimensions of the glass plate of a wedding photo are 18cm and 12cm respectively. A new frame of equal width is about to be fitted around the glass so that the area of the frame is the same as that of the glass. Find the width of the frame.
12. A group of acquaints went to a restaurants for a meal. When the bill for £175 was brought by a waiter, two of the cheeky ones from the group just sneaked off before the bill was paid, which resulted in the payment of extra £10 by each remaining individual. How many were in the group at first?
13. Ashwin and Donald decided to set out from two towns on their bikes, which are 247 miles apart, connected by a straight t Roman road in England. When they finally met up somewhere between the two towns, Ashwin had been cycling for 9 miles a day. The number of days for the whole adventure is 3 more than the number of miles that Donald had been cycling in a day. How many miles did each cycle?
14. When a two-digit number is divided by the product of the two digits, the answer is 2 and if 27 is added to the number, the original number turns into a new number with the digits being swapped around. Find the number.
15. There are three numbers: the difference of the differences of them is 5. The sum and product are 44 and 1950 respectively. Find the numbers.
16. Find the two numbers, whose sum is 19 and the product of the difference and the greater, is 60.
17. A boy was asked his age: "If you add the square root of it to half of it, and then subtract 12, the answer will be nothing," replied the boy. What was his age?
18. A group of army cadets, consisting of 1066 men, form two squares in front of a garrison. In the side of one square, there are 4 more men than the other. How many men are in each side of the squares?
19. The height of a triangle is 4cm less than three times its base length. If the area is 80 cm², find the lengths of the base and height.
20. An isosceles triangle is inscribed in a circle in such a way that its longest side, which goes through the centre is √50cm. Find the area of the triangle.
21. A butcher bought some pheasants for £100.00. Had each cost £1 less, he would have bought 5 more. How many pheasants did he buy?
22. The sum of reciprocals of two consecutive integers is 13/42. Find the integers.
23. The product of two numbers and the difference between them are 289 and 20 respectively. Find the numbers.
24. The sum of two numbers is 20. The sum of squares is 250. Find the numbers.
25. The area of a square exceeds twice that of another by 56cm². If the difference of the perimeter between the two is 24cm, find the area of the smaller square.

 

Answers

Move the mouse over, just below this, to see the answers:

1. 10, 12
2. 10cm, 24cm
3. 8cm
4. 5m
5. 4km/h
6. 10, 15
7. 1
8. 24cm, 24cm²
9. 5
10. 5 and 4
11. 3cm
12. 7
13. 117 and 130 miles
14. 36
15. 6, 13, 25
16. 12,7
17. 16
18. 21 and 25
19. 8cm, 20cm
20. 12.5cm²
21. 20
22. 6, 7
23. 27, 7
24. 15, 5
25. 100 or 4

 

Direct and Inverse Variation/Proportion

There are a few worked examples of the topic, shown below. In addition, there are a few questions for you to practise.

Direct Variation

When one quantity increases, if another quantity increases with that, it is called direct variation.
E.g.
The length of a rubber band (l) and the force that stretches it (F), are in direct variation.
l ∝ F
l = kF, where k is a constant.

Please move the slider and experiment with it.

l ∝ F

E.g.3

The length of a rubber band, when stretched by 20N is 6cm. Find the length, when the force is raised to 60N. Find the Force that keeps the length at 15cm.
l ∝ F
l = kF
When l = 6 and F = 20,
6 = k x 20
k = 6/20
When F = 60,
l = 6/20 x 60 = 18
F = 18 N.
When l = 15,
15 = 6/20 x F
F = 50N.

E.g.4

The power of a certain device (P) is directly proportional to the square of the current through it. The power is 60W, when the current is 2Amps. Find the power, when the current is 3Amps. Find the current when the power is 90W.
P ∝ I²
P = k I²
When I = 2 and P = 60,
60 = K X 4
k = 15
When I = 3,
P = 15 x 9
P = 135W.
When P = 90,
90 = 15 * I²
I = 2.3A.

Inverse Variation

When one quantity increases, if another quantity decreases with that, it is called inverse variation.
The volume of a fixed mass of gas is inversely proportional to the pressure.
V ∝ 1/P
V = k1/P

Please move the slider and experiment with it.

P ∝ 1 / V

E.g.5

The volume of a gas container is 3cm³ when pressure is 12Pa. Find the volume, when the pressure is 36N. At what pressure, will the volume be 9cm³?
When P = 12 and V = 3,
3 = k x 1/12
k = 36
When P = 36,
V = 36 x 1/36 = 1
V = 1cm³
When v = 9,
9 = 36 x 1/P
P = 4Pa.

E.g.6

The force between two magnets is inversely proportional to the distance between them. When the distance is 3cm, the force is 12N. Find the force, when the distance is 2cm. Calculate the distance, when the force is 432N as well.
F ∝ 1/d²
F = k 1/d²
When d = 3 and F = 12,
12 = k x 1/9
k = 108
When d = 2,
F = 108 x 1/4
F = 27N.
When F = 432,
432 = 108 x 1/d²
d² = 1/4
d = 1/2cm.

Now, in order to complement what you have just learnt, work out the following questions:

1. The distance d through which a feather falls from rest is proportional to the square of the time taken t. if the feather falls 15m in 3 seconds, how far will it fall in 9 seconds? How long will it take to fall 45m?
2. The energy E stored in a square-plated capacitor varies as the square of the length of the side x. When the length is 3cm, the energy stored is 81 Joules. What is the energy stored when the length is 5cm? What is the length when the stored energy is 243Joules?
3. The length L of an embryo of a certain mammal is proportional to the square root of the number of hours left before its birth. If the embryo is 12 cm long before 2 hours, how long will it be after 8 hours? How long will it take to grow to a length of 18cm?
4. p is directly proportional to q. Fill in the banks.
   

   p	q
   x	60
   4	12
   1/3	y

5. L is directly proportional to (M - 2). L is 36 when M is 4. Find L when M = 10. Find M when L = 108.
6. The kinetic energy of an object is proportional to the square of its speed. The kinetic energy is 64J when the speed is 4m/s. Find the kinetic energy when the speed is 20m/s. At which speed will the Kinetic energy be 900J?
7. The frictional force against the motion of a car is proportional to the square of the speed of the car. If this force is 16000N at 10 m/s, what is the force at 30 m/s? At what speed is the force equal to 900N?
8. The force of attraction between any two stars is inversely proportional to the square of the distance between them. The force between two, when they are 4 light years apart is 24x10⁶⁴N.Find the force when the distance is 3 light years. If the force is 48x10⁶⁴N, find the distance between them too.
9. In the following table, p is inversely proportional to q. Fill in the blanks.
   

   p	q
   x	60
   4	3
   1/3	y

10. y is inversely proportional to (x - 3). y = 4 when x = 5. Find y when x = 18. Find x when y = 144.

 

Statistics

Averages

The number chosen for representing a set of data is called its average. It must,

• • Represent all the values
• • Should not be an exaggerated one - not too small or not too big

There are three averages:

1. Mean
2. Mode
3. Median

Mean

This is the sum of all values divided by the number of data - Σ,sigma, means, add
Mean = ∑ x / n

Mode

This is the value that occurs most frequently.

Range of Data

The difference between the highest and lowest values is called the range of the data.

E.g. Data: 3, 4, 8, 6, 11, 21
Range = 21 - 3 = 18

Median

This is the middle value, when the data is arranged in order of size. Now, let's try some examples.

Finding Averages of Raw Data

Data that exists in the exact form since its collection is usually considered raw data.

E.g.1

The heights of five plants in a garden are 3cm, 4cm, 7cm, 12cm and 9cm. Find the averages.

Mean = ∑ x / n = 3 + 4 + 7 + 12 + 9 / 5 = 7cm
There is no mode, as each value occurs only once.
To find the median, let's rearrange them in order of size:
3, 4, 7, 9, 12
The middle value is 7. So, the median = 7cm.

E.g.2

The lengths of 6 carpets are 7m, 15m, 15m, 9m, 22m, 4m. Find the averages.

Mean = ∑ x / n = 7 + 15 + 15 + 9 + 22 + 4 / 6 = 12m
The mode = 15m
To find the median, let's rearrange them in order of size:
4, 7, 9, 15, 15, 22
The middle value = 9 + 15 /2 = 12, and so is the median.

Finding Averages of Tabular Data

Raw data, when arranged in a table for convenience, is in tabular form.

E.g.

The frequency of shoe sizes of students in a certain class is as follows:

shoe-size (x)	frequency (f)
3	3
4	5
5	10
6	8
7	4

Here, we have a slightly different approach;
Mean = sum of fx/n ∑ fx / n = 3X3 + 4X5 + 5X10 + 6X8 + 7X4 /30 = 5.2
TheMedian Class is the class where (n/2)^th value lies in. In this case, 30/2 = 15th value lies in shoe-size 5 class. So, it is the median class.
The Modal class is the class with the highest frequency. So, the modal class is shoe-size 5 class.

Finding Averages of Grouped Data

Raw data, when arranged in classes for easy handling, form grouped data. It is usually called a group frequency table.

E.g.

The marks obtained by a group of students for maths are as follows:

Marks (x)	frequency (f)
0 - 20	3
21 - 40	6
41 - 60	9
61 - 80	8
81 - 100	4

Mean = ∑ fx / n = 10X3 + 30X6 + 50X9 +70X8 + 90X4 /30 = 52.7 - x is the middle class value
The Median Class is the class where n/2 the value lies in. In this case, 30/2 = 15th value lies in 41 - 60 class. So, it is the median class.
The Modal class is the class with the highest frequency. So, the modal class is 41 - 60 class.

The reliability of the Mean

The mean can easily be influenced by the extremes values of data:

E.g

The heights of five plants are 2cm, 4cm, 7cm, 18cm, 19cm. Find the mean and comment on the result.
Mean = 2 + 4 + 7 + 18 + 19 / 5 = 10 cm
This value does not represent either the shortest plant - 2cm - or the tallest - 19cm. So, the mean in this case is not accurate; it may even mislead!

Probability

Possibility or likelihood of something happening is called probability.

Probability = no of events / total number of events

Toss a coin and you get Head and Tail:
P(Head) = 1/2  ;  P(Tail) = 1/2

Probability can take any value between 0 and 1, inclusive: if the event is certain to happen, the probability is 1; if the event is impossible, the probability is 0.

E.g.1

Nilup throws a die. Calculate the following probabilities:

1. Getting a prime number
2. Getting a number less than or equal 4
3. Getting a multiple of three

• P(prime) = 3/6 = 1/2
• P(number ≤ 4) = 4/6 = 2/3
• P(multiple of 3) = 2/6 = 1/3

E.g.2

Adam throws a die and toss a coin at the same time. Find the following probabilities:

1. Getting a Head and a prime number
2. Getting a Tail and a multiple of two
3. Getting a tail and an odd number

• P(Head and Prime) = 3/12 = 1/4
• P(Tail and multiple of two) = 3/12 = 1/4
• P(Tail and odd number) = 3/12 = 1/4

E.g.3

The letters of the word CHAOS are placed in a container. Calculate the following probabilities.

1. Getting a vowel
2. Getting a consonant
3. Getting a letter from the first half of the alphabet

• P(Vowel) = 2/5
• P(Consonant) = 3/5
• P(Letter from the First Half) = 3/5

E.g.4

Three red balls, two green balls and five blue balls are in a container. Calculate the following probabilities:

1. Getting a red ball
2. Getting a red or blue ball
3. Not getting a blue ball

• P(Red) = 3/10
• P(Red or Blue) = 8/10 = 4/5
• P(Not getting a blue) = 5/10 = 1/2

E.g.5

A coin is tossed three times. Find the following probabilities:

1. Getting three Heads
2. Getting at least two heads
3. Getting two Heads and a Tail

The space diagram looks like this - HHH; HTT; HHT; HTH; TTH; THT; TTT; THH

• P(three Heads) = 1/8
• P(at least two heads) = 4/8 = 1/2
• P(two Heads and a Tail) = 3/8

 

E.g.6

Two dice are thrown. Find the following probabilities.

1. Getting two equal numbers
2. The sum of the two numbers being less than 7
3. Getting at least one even number

1. 6/36 = 1/6
2. 15/36 = 5/12
3. 27/36 = 3/4

 

 

Mutually Exclusive Events

If two events cannot happen at the same time, they are said to be mutually exclusive.

E.g.

Someone throws a die; look at the following events:

• Event A - getting a prime number
• Event B - getting number 2
• Event C - getting an odd number

A and B can happen at the same time - not mutually exclusive.
A and C can happen at the same time - not mutually exclusive.
B and C cannot happen at the same time - mutually exclusive.

Do you find difficulty to remember this? Think of day and night - they are mutually exclusive.

'OR' rule for Mutually Exclusive Events

If Event A and Event B are mutually exclusive,
P( A or B ) = P(A) + P(B)

E.g.
Gehan throws a die. Calculate the probability of getting number 2 or an odd number.
P(2) = 1/6; P(odd) = 1/2
Since these two events are mutually exclusive,
P(2 or Odd) = 1/6 + 1/2 = 4/6 = 2/3

Independent Events

If one event does not influence another event, they are said to be Independent.

E.g.
You throw a die and toss a coin. The outcome of coin does not affect that of die and vice versa; so, these events are independent.

However, now look at the following events:

• Event A - you go to school by bus in time
• Event B - the bus is late

Event A and Event B are not independent; B certainly influences A.

'AND' rule for Independent Events

If Event A and Event B are independent,

P( A and B ) = P(A) X P(B)

E.g.
Natalie throws a die and toss a coin. Calculate the probability of getting a Head and an even number.
P(Head) = 1/2; P(even) = 1/2
Since these two events are independent,
P(Head and even) = 1/2 x 1/2 = 1/4

 

Any comments? Please drop a line.