Trigonometric Curves

The three main trigonometric graphs are:

• Sine graph
• Cosine graph
• Tan graph

Sine Graph

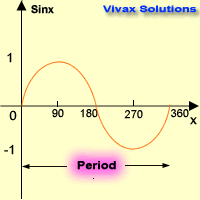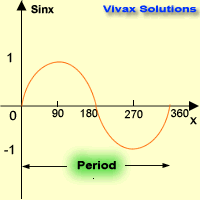
x0	sin x
0	0
90	1
180	0
270	-1
360	0

Characteristics:

• Period is 360⁰. It repeats itself every 360 degrees.
• Maximum value = +1
• Minimum value = -1

Cosine Graph

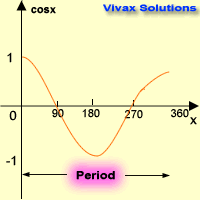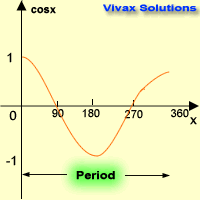
x0	cos x
0	1
90	0
180	-1
270	0
360	1

Characteristics:

• Period is 360⁰. It repeats itself every 360 degrees.
• Maximum value = +1
• Minimum value = -1

Tan Graph

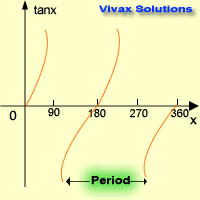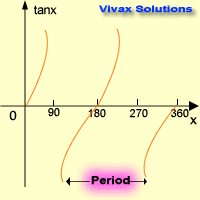
x0	tan x
0	0
90	∞
180	0
270	∞
360	0

Characteristics:

• Period is 180⁰. It repeats itself every 180 degrees.
• Maximum value = +∞
• Minimum value = -∞

Practice for Trigonometric Curves - interactive

You may move the grid so that you can see the behaviour of the curves for the bigger values of the angles - on both sides.

Transformation of a Graph

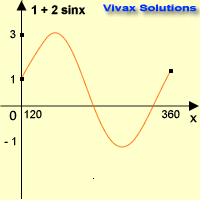
x0	sin x	2 sin x	1 + 2 sin x
0	0	0	1
90	1	2	3
180	0	0	1
270	-1	-2	-1
360	0	0	1

This is stretched by a factor 2 parallel to the y-axis and then moved up by 1 - a translation of 1 in the positive y-axis.

Now, in order to complement what you have just learnt, work out the following questions:

>

1. Sketch the following graphs:
   • 2 cos x
   • 1 - 3 sin x
   • 2 tan x
   • 2 + 3 sin x
2. Find the period, maximum value and minimum value of the following functions:
   • 3 cos x
   • 1 - 2sin 2x
   • 3 cos 2x
   • 2 + 3 sin x/2