Straight-line Graphs

In this tutorial, you will learn the following in detail interactively:

We all know how straight line graphs span across graph papers - or grids. These graphs have two things in common. They are Gradient and Intercept.

Gradient - m

 

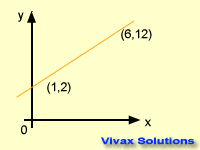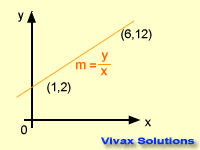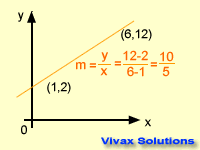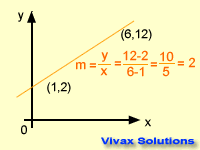
The slope or steepness of a graph is called the gradient. It is calculated by dividing a change in 'y' by change in 'x' between two points.

 

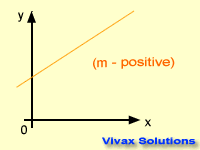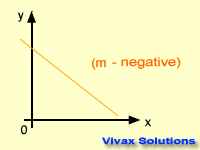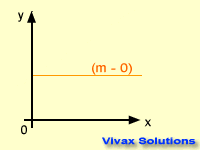
The gradient can be positive, negative or zero.

Intercept - c

 

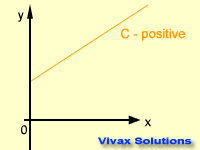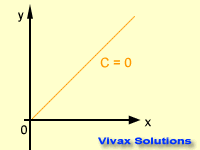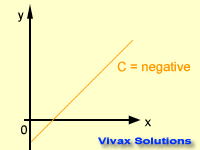
This is the distance between the origin of a graph and the point where it crosses the y-axis. The intercept can also be negative, positive or zero.

You can practise the above concepts interactively in the following applet; choose an intercept value and then click the play button and watch.

 

The Equation of a Straight Line

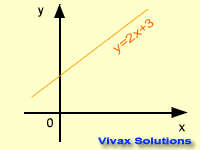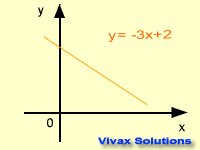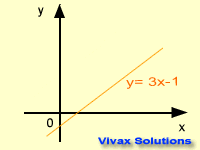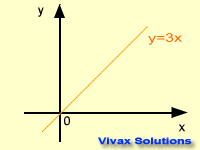
y = mx + c is the equation of a straight line. Any straight line can be expressed in this form where 'm' and 'c' are gradient and intercept respectively. The graph takes its shape, depending on the values of the gradient and the intercept. This following animation shows that.

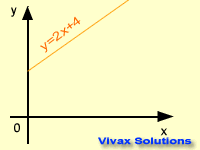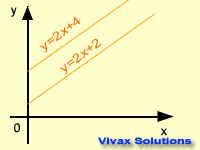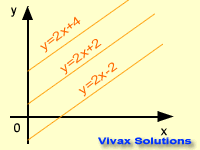
The gradients of parallel lines are the same; the product of the gradients of perpendicular lines is
-1.

E.g.1

The gradient of a straight line is 2. It passes through (3,4). Find its equation.
y = mx + c
4 = 2 X 3 + c
4 = 6 + c
c = -2
The equation is, y = 2x - 2.

E.g.2

The gradient of a straight line is -3. It passes through (-2,4). Find its equation.
y = mx + c
4 = -3 X -2 + c
4 = 6 + c
c = -2
The equation is, y = -3x - 2.

E.g.3

A straight line passes through (2,5) and (4, 11). Find its equation.
m = (11 - 5) / (4 - 2) = 6 / 2 = 3
y = mx + c
x = 2, y = 5, m = 3,
5 = 3 X 2 + c
5 = 6 + c
c = -1
The equation is y = 3x - 1.

E.g.4

The equation of a straight line is y = 3x -2. Find the equation of a second line that passes through (4,-3), parallel to the first line.
Since the two lines are parallel, the gradients are the same. For the second line,
x = 4, y = -3, m = 3
-3 = 3 X 4 + c
-3 = -12 + c
c = 9
The equation is y = 3x + 9.

E.g.5

The equation of a straight line is y = 2x -3. Find the equation of a second line that goes through (4,-5), at right angles to the first line.
If the gradient of the second line is m, then 2 X m = -1; => m = -1/2
For the second line,
x = 4, y = -5, m = -1/2
-5 = 4 X (-1/2) + c
-5 = -2 + c
c = -3
The equation is y = -1/2 x - 3.

 

E.g.6

The equation of a straight line is 2y = 3x - 8. Find the equation of a parallel line that goes through (4,3).
Let's rearrange the equation in y = mx + c form.
So, y = 3/2 x - 4 If the gradient of the line is m, then m = 3/2;
For the second, parallel line,
x = 4, y = 3, m = 3/2
3 = 4 X (3/2) + c
3 = 6 + c
c = -3
The equation is y = 3/2 x - 3. or 2y = 3x - 6

 

E.g.7

The equation of a straight line is 3y = 2x -12. Find the equation of a second line that goes through (4,-5), at right angles to the first line.
Let's rearrange the equation in y = mx + c form.
y = 2/3 x - 4
If the gradient of the second line is m, then 2/3 X m = -1; => m = -3/2
For the second line,
x = 4, y = -5, m = -3/2
-5 = 4 X (-3/2) + c
-5 = -6 + c
c = 1
The equation is y = -3/2 x + 1.

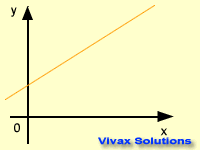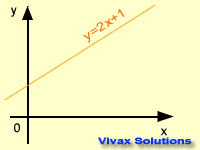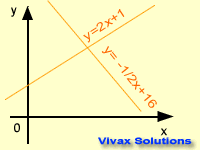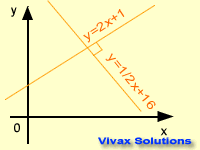
Parallel Lines and Perpendicular Lines

If two lines are parallel, they have the same gradient.If two lines are perpendicular, the gradient of one line is the negative reciprocal of the other; it's also called, the normal.

You can practise the concept below; just move the point, A, and see how gradients change:

 

 

E.g.1

The equation of a straight line is y = 2x - 3. Find the equation of a parallel line that goes through, (4,7).
Since they are parallel, for the second line, m = 2
y = mx + c
7 = 2(4) + c
7 = 8 + c
c = -1
y = 2x - 1

E.g.2

The equation of a straight line is y = 4x - 5. Find the equation of a perpendicular line that goes through, (4,7).
Since they are perpendicular, for the second line, m = -1/4
y = mx + c
7 = (-1/4)4 + c
7 = -1 + c
c = 8
y = (-1/4)x + 8

E.g.3

The equation of a straight line is y = (-1/2)x - 5. Find the equation of a perpendicular line that goes through, (8,7).
Since they are perpendicular, for the second line, m = 2
y = mx + c
7 = (2)8 + c
7 = 16 + c
c = -9
y = 2x - 9

E.g.4

The equation of a straight line is 2y = 3x - 8. Find the equation of a parallel line and a perpendicular line that go through, (6,8).
By rearranging equation,
y = (3/2)x - 4
For a parallel line, m = 3/2
y = mx + c
8 = (3/2)6 + c
8 = 9 + c
c = -1
y = (3/2)x - 1
For a perpendicular line, m = -2/3
y = mx + c
8 = (-2/3)6 + c
8 = -4 + c
c = 12
y = (-2/3)x + 12

Equation of the Tangent to a Curve

With the following interactive animation, you can easily master maths behind the equation of a tangent to a curve.

E.g.

 

 

Find the equation of the circle and the equation of the tangent to the curve at point, A(4,3).
The coordinates of the point, A, are(4,3)
If the radius of the circle is r, r² = 4² + 3²,
r = 5
The equation of the circle: x² + y² = 5²
The gradient of the radius = 3/4
Since the tangent is perpendicular to the radius at A,
Gradient of the tangent = -4/3
For the tangent,
x = 4, y = 3, m = -4/3
3 = -(4/3)x4 + c
3 = -16/3 + c
c = 25/3
y = -4/3 x + 25/3
3y = -4x + 25
4x + 3y = 25 or y = (-4/3)x + 25/3
Now, change the radius with the slider - and the coordinates of A - and find the equations of new tangents and radii of the circle.

 

Length of Line Segment and Coordinates of Mid-Point

The length of the line segment can be calculated by using the Pythagoras' Theorem. The coordinates of the mid-point is given by the average of the coordinates of the two points.

 

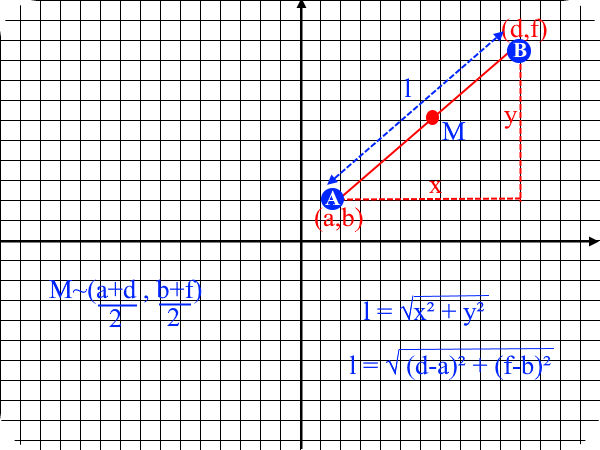
E.g.1

The coordinates of A and B are (2,5) and (5,9) respectively. Find the length and the coordinates of the mid-point.

M ~ ((2+5)/2, (5+9)/2)
M ~ (3.5,7)
l = √(5-2)² + (9-5)²
l = 5

E.g.2

The coordinates of A and B are (-7,4) and (5,9) respectively. Find the length and the coordinates of the mid-point.

M ~ ((-7+5)/2, (4+9)/2)
M ~ (-1,6.5)
l = √(5--7)² + (9-4)²
l = √12² + 5²
l = 13

E.g.3

The coordinates of A and B are (-2,8) and (1,4) respectively. Find the length and the coordinates of the mid-point.

M ~ ((-2+1)/2, (8+4)/2)
M ~ (-0.5,6)
l = √(-2-1)² + (8-4)²
l = √3² + 4²
l = 5

 

Now, in order to complement what you have just learnt, work out the following questions:

Find the equations of the following graphs - use the button to get a pair of coordinates.