Quadratic Equations

Quadratic Equations: Your GCSE & IGCSE Mastery Guide (4 Methods Included!)
Feeling a little lost in the world of quadratics? Don't worry, you're not alone! Quadratic equations are a fundamental concept in GCSE and IGCSE maths, but solving them can feel tricky. But fear not, intrepid student! This comprehensive guide will equip you with not one, but **FOUR** powerful methods to tackle any quadratic equation with confidence.
Whether you're a whiz at factoring or prefer a more formulaic approach, we've got you covered. We'll break down each method step-by-step with clear explanations and helpful examples. By the end of this tutorial, you'll be a quadratic-conquering champion, ready to ace those exams!

In this tutorial, you will learn:

Quadratic Equations

An equation in the form of ax² + bx + c = 0 is called a quadratic equation.

E.g.

• x² + 6x + 8 = 0
• 2x² - 5x + 6 = 0
• x² - 6 = 0
• x² - 6x = 0

A quadratic equation has two solutions; that means there are two values for x that satisfy the equation. There are four different ways to solve a quadratic equation:

1. Factorizing Method
2. Formula Method
3. Graphical Method
4. Completing the Square Method

Factorizing

E.g.1
x² + 8x = 0
x(x + 8) = 0
x = 0 or (x + 8) = 0
x = 0 or x = -8

E.g.2

x²= 6x
x² - 6x = 0
x(x - 6) = 0
x = 0 or (x - 6) = 0
x = 0 or x = 6

E.g.3

x² + 6x + 8 = 0
x² + 4x + 2x + 8 = 0
x(x + 4) + 2(x + 4) = 0
(x + 4)(x + 2) = 0
(x + 4) = 0 or (x + 2) = 0
x = -4 or x = -2

E.g.4

x² - 6x + 8 = 0
x² - 4x - 2x + 8 = 0
x(x - 4) - 2(x - 4) = 0
(x - 4) = 0 or (x - 2) = 0
x = 4 or x = 2<

E.g.5

x² + 6x - 16 = 0
x² + 8x - 2x - 16 = 0
x(x + 8) - 2(x + 8) = 0
(x + 8) = 0 or (x - 2) = 0
x = -8 or x = 2

E.g.6

2x² + 13x + 6 = 0
2x² + 12x + x + 6 = 0
2x(x + 6) + 1(x + 6) = 0
(x + 6) = 0 or (2x + 1) = 0
x = -6 or 2x = -1
x = -6 or x = -1/2

E.g.7

x² - 9/4 = 0
(x + 3/2)(x - 3/2) = 0
x + 3/2 = 0 or x - 3/2 = 0
x = -3/2 or x = 3/2

Formula Method

If ax² + bx + c = 0, then
x = [-b ±√(b² - 4ac) ]/ 2a

E.g.1

x² - 6x + 8 = 0
a = 1; b = -6; c = 8
x = -(-6) ±√((-6)² - 4(1)(8)) / 2(1)
x = 6 ±√(36 - 32) / 2
x = 6 ±√(4) / 2
x = (6 ± 2 )/ 2
x = 4 or x = 2

E.g.1

2x² - 5x + 3 = 0
a = 2; b = -5; c = 3
x = -(-5) ±√((-5)² - 4(2)(3)) / 2(2)
x = 5 ±√(25 - 24) / 4
x = 5 ±√(1) / 4
x = (6 ± 1 )/ 4
x = 1.5 or x = 1

 

Graphical Method

In this method, a graph is plotted for a quadratic function. The graph takes the typical shape, known as parabola.

E.g. Solve x² + 5x - 7 = 0

First of all, make a table for both x and y of the function.

x	y
-2	-13
-1	-11
0	-7
1	-1
2	7
3	17

 

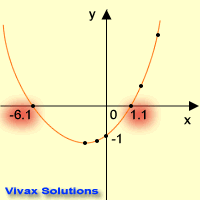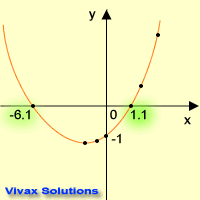
Now, plot a graph of y against x. Note the points at which the curve the crosses the x-axis. They are the solutions of the quadratic function. The solutions are:
x = 1.1 or x = -6.1

The following animation is interactive: it shows how to solve a quadratic equation by a graph; by clicking on the button, you can generate a random equation and its solutions appear at the same time. If there are no solutions - the graph being above the x-axis - instead of solutions, the word, undefined, appears in those places.

 

 

Completing the Square Method

x² + 4x - 5 = 0
Let (x + a)² + b = x² + 4x - 5
x² + 2ax + a² + b = x² + 4x - 5
Now, make the coefficients of x and the constant equal.
x => 2a = 4
a =2
a² + b = -5
4 + b = -5
b = -9
(x + 2)² - 9 = 0
(x +2)² = 9
(x + 2) = ±3
x = -2 ±3
x = 1 or -5

 

Now, in order to complement what you have just learnt, work out the following questions:

Click the button to get the quadratic equations; solve them by all four methods to master the techniques.