Functions and Transformation of Graphs
Feeling lost in the world of graph transformations for your GCSE or IGCSE Maths?
Struggling to visualize how adding, subtracting, multiplying, and dividing affects the position and shape of a function's graph?
Worry no more! This interactive tutorial breaks down graph transformations into easy-to-understand concepts with clear explanations, step-by-step worked examples,and engaging simulations.
By the end of this guide, you'll be confidently transforming graphs like a pro, feeling prepared to ace your exams!
You will interactively learn the following:
- What a function is
- Three types of transformation of functions
- Translation of graphs
- Reflection of graphs
- Stretching of graphs
- Interactive simulations to practise transformations
- Worked examples to master the concept
Functions
y = x2 + 3x -2 is said to be a function of x - an expression of x. This can also be written, in a bit more advanced way as f(x) = x2 + 3x -2 -
it is read as you write, function of x, f(x)
So, f(x) = x2 + 3x -2
Now whatever you put in as 'x' on the left, substitutes 'x' on the right.
E.g.
- f(2) = 22 + 3x2 -2 = 4 + 6 - 2 = 8
- f(-2) = (-2)2 + 3x(-2) -2 = 4 - 6 - 2 = -4
- f(0) = 02 + 3x0 -2 = 0 + 0 - 2 = -2
- f(x+1) = (x+1)2 + 3(x+1) -2 = x2 + 2x + 1 + 3x + 3 -2 = x2 + 5x + 2
- f(x-1) = (x-1)2 + 3(x-1) -2 = x2 - 2x + 1 + 3x - 3 -2 = x2 + x - 5
- f(2x) = (2x)2 + 3(2x) -2 = (2x)2 + 6x -2 = 4x2 + 6x - 2
- f(x/2) = (x/2)2 + 3(x/2) -2 = x2/4 + 3x/2 -2 = x2/4 + 3x/2 - 2
There are three major transformations:
- Translation
- Reflection
- Stretching
Let's apply the above transformations to the following curve.
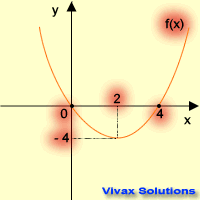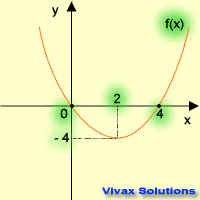
Translation
| f(x) -----> f(x+1) | f(x) -----> f(x-1) |
|---|
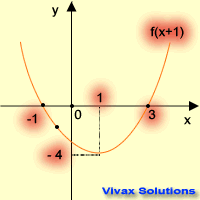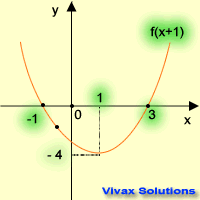 | 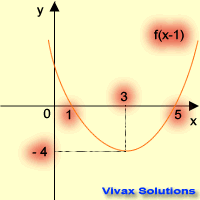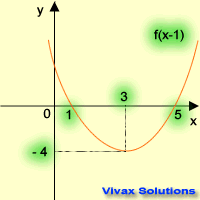 |
| translation in the -ve x-axis | translation in the +ve x-axis |
| f(x) -----> f(x) + 2 | f(x) -----> f(x) - 2 |
|---|
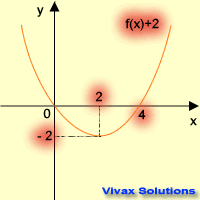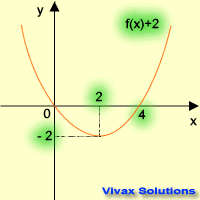 | 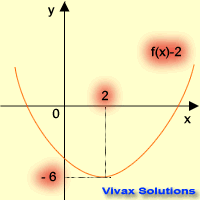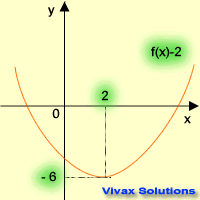 |
| translation in the +ve y-axis | translation in the -ve y-axis |
You can animate the following curves to see how translation works. Please select an option and then move the sliders.
Choose slider, a, for the translation in the x-axis.
Choose slider, c, for the translation in the y-axis.
Reflection
| f(x) -----> f(-x) | f(x) -----> -f(x) |
|---|
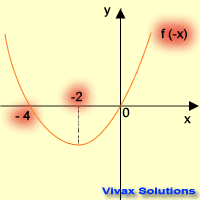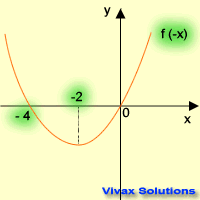 | 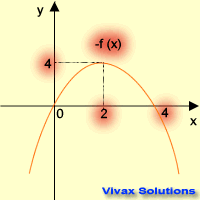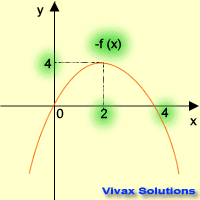 |
| reflection in the y-axis | reflection in the x-axis |
Stretching
| f(x) -----> f(2x) | f(x) -----> 2f(x) |
|---|
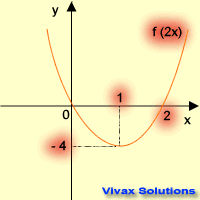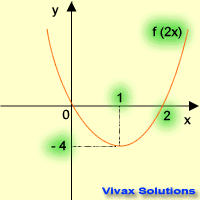 | 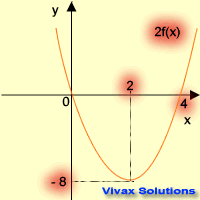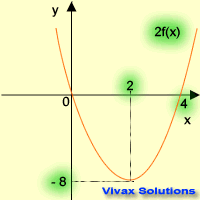 |
| stretching parallel to x-axis | stretching parallel to y-axis |
You can animate the following curves to see how stretching works. Please select an option and then move the sliders.
Choose slider, a, for the stretching parallel to y-axis.
Choose slider, c, for the stretching parallel to x-axis.
Now, let's apply the transformation to some of the well-known curves.
E.g.1
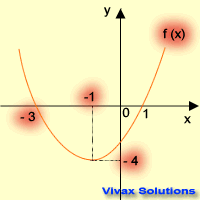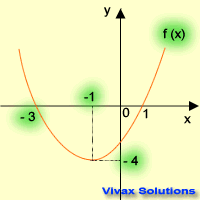
Sketch f(x) = x2 + 2x -3, and find the following:
- line of symmetry
- minimum value
- translations from f(x) = x2
- solutions
First of all, let's use the completing the square method:
Let x2 + 2x -3 = (x+a)2 +b
x2 + 2x -3 = x2 + 2ax + a2+ b
Make the coefficients of x2, x and the constant on either side equal.
2a = 2 => a = 1
a2+ b = -3 => b = -4
f(x) = (x+1)2 -4
Line of symmetry, x = 1
Minimum value = -4
This is a translation of f(x) = x2, 1 in the negative x-axis and 4 in the negative y-axis.
The solutions are, x = -3 and x = 1
E.g.2
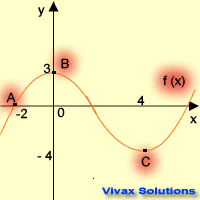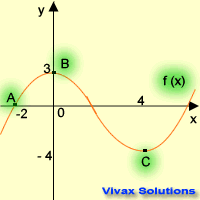
This question is based on the curve above; its equation is, f(x) = (x+4)(x-3)(x-2). Find the coordinates of A, B and C after the following
transformations. The answers are on the table.
| Transformation | New Coordinates |
|---|
| f(x+1) | A( -4 , 6 ) | B( 0 , -30 ) | C( 2 , 0 ) |
| f(x-1) + 2 | A( -2 , 8 ) | B( 1 , -22 ) | C( 4 , 2 ) |
| f(2x) | A( -1.5 , 6 ) | B( 0 , -24 ) | C( 1.5 , 0 ) |
| f(x/2) | A( -6 , 6 ) | B( 0 , -24 ) | C( 6 , 0 ) |
| 2f(x) | A( -6 , 12 ) | B( 0 , -48 ) | C( 3 , 0 ) |
| f(-x) | A( 3 , 6 ) | B( 0 , -24 ) | C( -3 , 0 ) |
| -f(x) + 2 | A( -3 , -4 ) | B( 0 , 26 ) | C( 3 , 2 ) |
Combination of Transformations
Here is an opportunity for you to practise transformations using a sine curve. The curve is in the form of
y = a + b sin(cx + d). Change the values of a, b, c and d or to see the corresponding change. This is the best form of mastering the transformations.
Now, in order to complement what you have just learnt, work out the following questions:
- Use the completing the square method to sketch f(x) = x2 + 3x -4. Then describe the transformations of f(x) = x2 to get this particular shape. Write down the
minimum value and the line of symmetry too.
- Show that the reflection in the y-axis of f(x) = x4 - 2x2 + 5 is the same as f(x).
- Write down a function that shows f(x) = -f(-x). Hence, sketch 2f(x) and f(2x) of the same function.
- If f(x) = x2 + 2x, sketch the following:
- f(-x)
- -f(x) + 2
- f(x+2) - 3
- f(2-x)
- 2f(x) + 1
- f(2x) - 3
- Sketch f(x) = x2 -x - 6 and hence sketch g(x) = (x+2)(x+3) and show that f(x+1) = g(x).
- Sketch f(x) = 1 +2 sin(x) and solve f(x) = 1.3 for 0 < x < 360. What is the minimum value and maximum value of the function?<
- Sketch f(x) = 1 + cos(3x) and hence find the period of the function, maximum value and minimum value.
- Sketch f(x) = 3 - 2sin(3x) and hence find the period of the function, maximum value and minimum value.
- Sketch f(x) = 1/x and then transform as follows:
- f(-x) + 2
- -f(x) + 2
- 2f(x) - 3
- The maximum value of f(x) = q + p cos(x) graph is 7 and the minimum is 1. find p and q.