
Very hard questions for GCSE Maths
Do you need highly challenging questions for GCSE Maths exam? Here are some. Take the plunge and see whether you can crack them! They are from:
- Numbers
- Algebra
- Geometry
- Trigonometry
- Data handling
- Vectors
- Probability
- And many more...
Answers are at the bottom of the page. ↓
Question 1
If x² + y² = 13 and x + y = 5, find (x - y)², clearly showing the steps.
Question 2
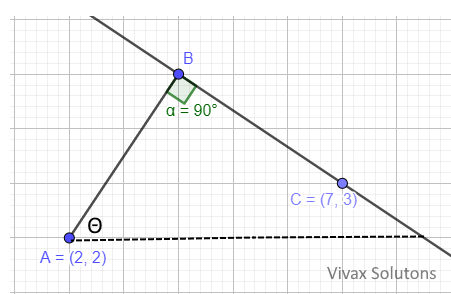
If tan Θ = 3/2, find the equation of the line that goes through B and C. Leave your answer in the form of ax + by = c, where a, b and c are integers. Hence find the coordinates of B.
Question 3
a)
A group of girls in a class shared a bill for £22.09, equally between them. How many girls were there in the group? How much did it cost each?
b) u = v - ft/m is a formula in which v f, m and t are 18, 12, 6, 3, each correct to 1 significant figure. Find the lower and upper bound of u. Hence, provide a good approximation for u.
Question 4
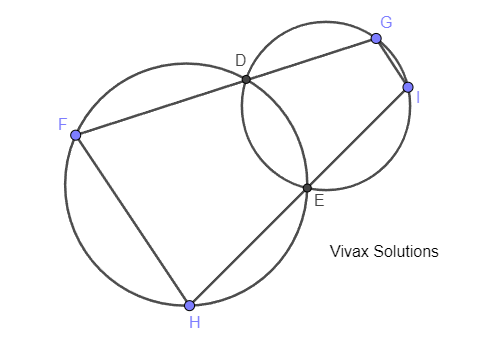
a) The two circles intersect at D and E. Prove that the sides FH and GI are parallel.
b) The radii of the two circles are 8 cm and 6 cm respectively. If the centres of the large and small circles are A and C respectively, find the angle between AD and DC, if AC = 12 cm.
Question 5

A twelve-sided, fair die is rolled n times. Find the probability of getting 1 in two successive throws. How do you justify your answer? Hence find the probability of getting at least number 1 once, if the die
is thrown n times.
Question 6
a) A cyclist covers two sections of a road, 10 miles and 15 miles, at 5 mph and 3 mph respectively. Find his average speed.
b) In another cycle ride, he covers one half of a certain distance at 10 mph and the rest at 15 mph respectively. Find his average speed.
Question 7
a) Ted gave £1400 to share between his children, Berty, Clare and Damion in such a way that Berty gets twice as much as Clare and Damion gets half of what Clare gets. How much does Clare get?
b) If it takes 8 workers 6 days to build a wall 6 meters high, how many workers are needed to build a wall 9 meters high in 9 days?
Question 8
a) If x(x - 2) : x² - 6x + 8 = 7 : 3, find the value of x.
The ages of three siblings, A, B, and C, are in the ratio 3:4:7 respectively. The sum of their ages is 84 years.
b) Determine the age of each sibling.
c) If n years ago, C was twice as old as B was then, Find n.
Question 9
If 2x² + 4x + 1 ≡ a(x + b)² + c,
a) find a, b and c.
b) Find the line of symmetry of the curve.
c) Find the coordinates of the minimum point of the curve.
d) Find the y-intercept.
e) Find the values of x where the curve crosses the x-axis.
f) If the curve is brought down by p, the solutions of the equations become x = 0 and x = -2. Find p.
Question 10
The numerator of a fraction is 2 less than its denominator. If both numerator and denominator are increased by 2, the fraction becomes 7/9. Find the original fraction.
Question 11
Two trains remained stationary on the same track 90 km apart, facing each other. They started moving towards each other at constant speeds, 40km/h and 20 km/h, respectively. As soon as they started moving, a bird started flying from one train to the other and vice versa at
50 km/h until the two trains just managed to stop next to each other in time. Find the total distance that the bird had flown by then?
Question 12
Please use a pair of compasses and a ruler for the following constructions. You may use a protractor only for verifying the angles.
a) Construct an angle of 105°.
b) Construct a regular octagon inside a circle.
c) The three sides of the triangle, ABC, are 5 cm, 12 cm and 13 cm respectively. Construct the triangle. Hence construct a circle that touches the vertices, A, B and C. Find the area of the circle as well.
Question 13
The equation of a curve is f(x) = ax² + bx + c and f(-1), f(2) and f(3) are 10, 7 and 14 respectively. Find a, b and c.
Question 14
A courier driver has 72 parcels in his van. At a certain store, he drops 2 parcels and x were collected. At the next store, he drops a fifth
of the parcels, before collecting 4. If he has 64 parcels in his van at this stage, find x.
Question 15
a) Find the exact value of 202² - 198² without long multiplication.
b) Fully factorize x3 + 6x² - 4x - 24
Question 16
a) Three coins are tossed. Find the probability of getting at least 2 heads.
b) There are n balls in a container. Two of them are
black and the rest are white. A ball is taken out
at random, its colour noted and put back in.
Then a second ball is taken and the steps are
repeated. The probability of getting two balls of
different colours is 12/25. Show that 3n² - 25n +
50 = 0 and calculate the number balls in the
container.
Question 17
The nth term of a sequence of triangular numbers is
given by the formula, (n² + n)/2. Prove that the sum of
any two consecutive triangular numbers is a square
number.
Question 18
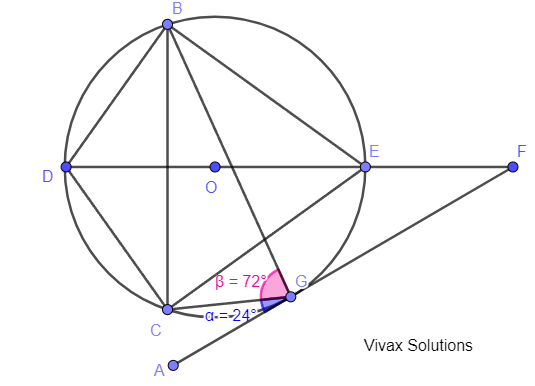
a) Find the angle BOC.
b) find the angle BCG.
c) If BE = EC, find the angle EBG.
Question 19
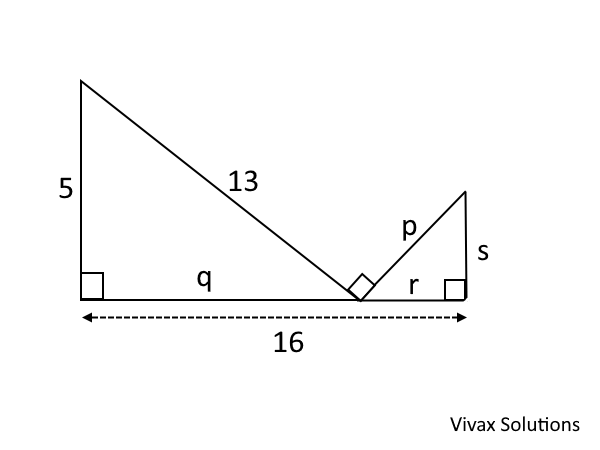
In the above diagram, find the value of length p.
Question 20
a) The mean of the numbers, 4, 5, 10, 11 , Y, is the same as the median of the numbers. Find Y.
b) The mean score for maths of 6 girls is 72 and that for 4 boys is 60. Find the mean score of the whole group. If two boys are added to the group with scores, 67 and 81, find the new mean of the group.
Question 21
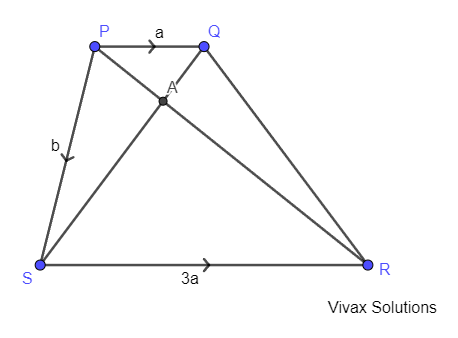
PQRS is a trapezium with PQ being parallel to SR. The vectors, PQ = a, PS = b and SR = 3a. PA = PR/4.
a) Find the vectors, PR, PA, SA and SQ.
b) Show that the points, S, A and Q lie on the same straight line.
Question 22
a) If p : q = 4 : 5 and q : r = 3 : 2, find p : q : r.
b) If a : b = 3 : 5 and 3b : c = 4 : 7, find a : b : c.
Question 23
a) Solve x4 - x² = 6 and leave the answer in surd form.
b) Solve x - 7√x + 12 = 0 .
Question 24
a) Prove that the area of a kite is half of the product of the diagonals.
b) The coordinates of the points, A, B and C are (4 , 6), (8 , 4) and (5 , 3) respectively. Find the area of the triangle ABC.
Question 25
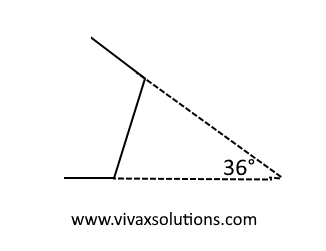
If the angle between the two extended sides is 36°, find the number of sides of the regular polygon. If the length of a side is 5cm, find its area.
Question 26
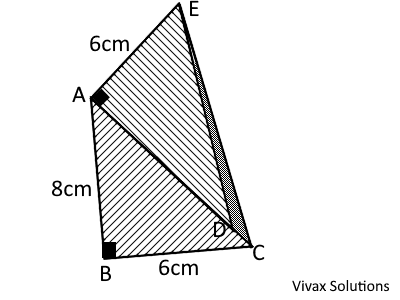
Find the area and the perimeter of triangle EDC, if the above composite shape consists of two identical triangles, ABC and ADE.
Question 27
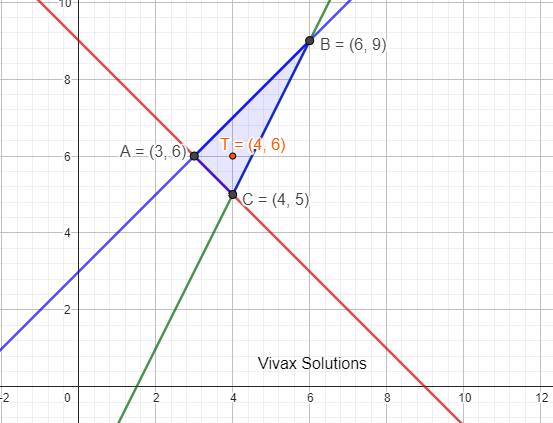
Find the shaded area and the three inequalities that satisfy the region.
Question 28
a) Find the value of 1/x, when x approaches infinity.
b) Hence, find the value of (n+1)/(n-1), when n gets really large.
Question 29
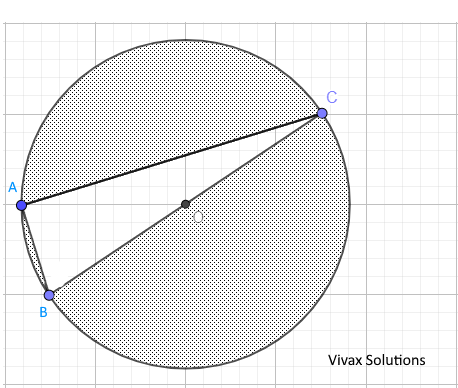
In the above diagram, AB = 7 cm and AC = 24 cm, find the shaded area, if O is the centre of the circle.
Question 30
Prove that the sum of the squares of diagonals of a parallelogram is twice the sum of the squares of the two adjacent sides.
Question 31
The length of a wire is 64cm and it is divided into n equal parts. The sum of the reciprocals of the lengths is equal to 1. Find the value of n.
Question 32
a) If f(x) = 2x - 3 and g(x) = (x + 3)/2, show that gf(x) = fg(x).
b) If h(x) = x² - 2x, find h-1(x).
Question 33
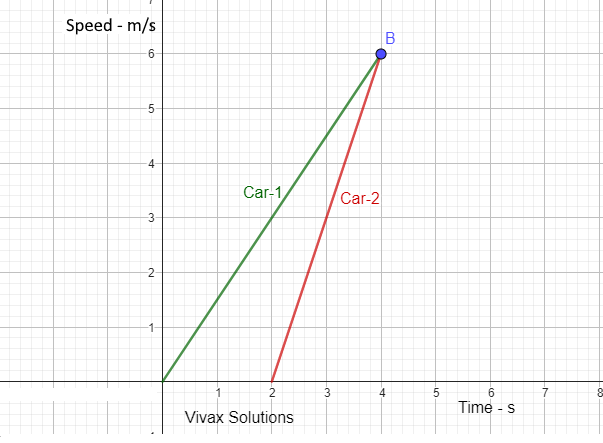
Two cars, Car-1 and Car-2, move as shown above. Both start from rest with a time interval 2 seconds. Both cars accelerate.
a) What is the significance of point B? Explain your answer.
b) Do they meet up at B? Justify your answer.
c) Find the acceleration of each car.
Question 34
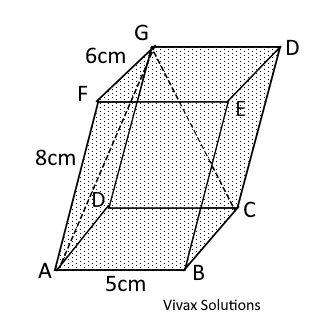
Find the angle of AGC of the triangle CGA, without the use of the cosine rule. You may use basic trigonometry.
Question 35
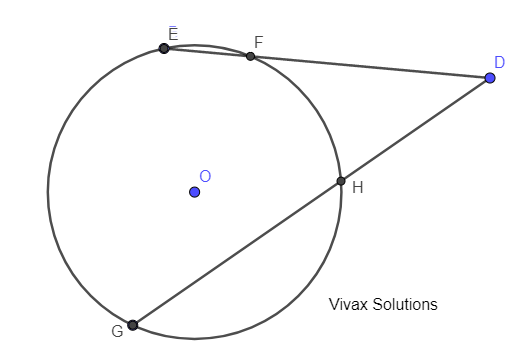
In the above diagram, ED = 6.69cm, GD = 8.88cm, HD = 3.7cm. Find the length of FD.
Question 36
The equation of a trigonometric curve is f(x) = a sin(x) + b, where a > b > 0. The maximum and minimum values of the functions are 7 and -3 respectively.
a) Sketch the graph, showing a and b clearly on the grid.
b) Find a and b.
c) Describe the transformation of f(x), from y = sin(x).
Question 37
a) Solve (2n)n X (1/8)n X 1/16 = 1, if n > 0.
b) Solve 32(x+2)/(x+7) = 1/8
Question 38
a) Show that the curve y = x² - 2x and the line y = 4x - 9 intersect only at one point.
b) Find the coordinates of the above point, A.
b) Find the distance between the point A and the y-intercept.
Question 39
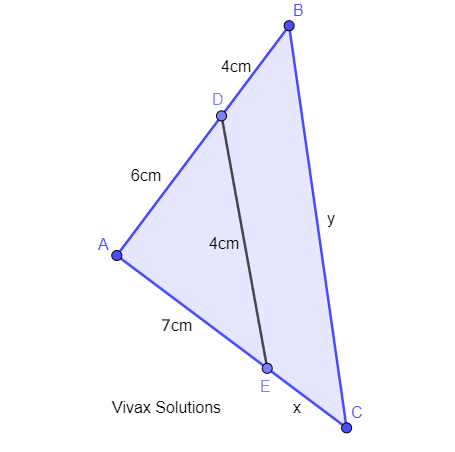
The triangles, ABC and ADE, are similar.
a) Find x.
b) Find y.
Question 40
The masses of two similar solid cylinders, made of the same substance, are 7 kg and and 189 kg respectively.
a) If the height of the shorter cylinder is 6 cm, find the height of the taller cylinder.
b) Find the ratio of the surface areas of the cylinders.
Question 41
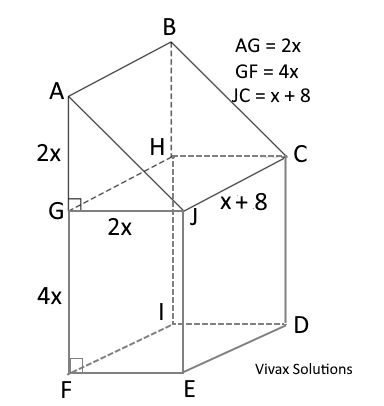
The composite object consists of two sections - a section with a triangular cross section and a rectangular cross section. The volume of the former is ¼ th of the latter. The lengths are in cm.
a) If the volume of the object is 10x3 + 720, find x.
b) If a liquid pours into the object at 33 cm3/min, how long will it take to fill it to a 1/6 the of its maximum height?
Question 42
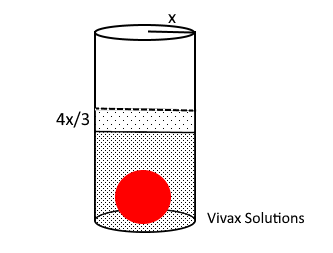
a) When the sphere is dropped into the liquid in the cylinder, the height of the liquid goes up by 4/3 the of the radius of the cylinder. Prove that the radius of the sphere is the same as that of the cylinder.
b) If the height of the liquid in the cylinder is 4 times its radius, find the ratio of volume of the liquid to the volume of the sphere.
Question 43
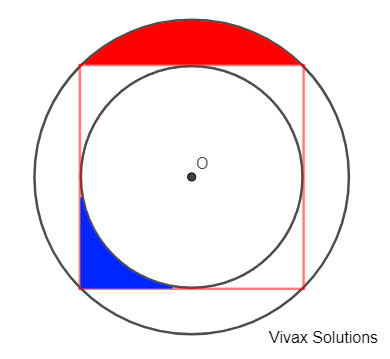
The centres of the two circles and the square are the same.
a) Prove that the area of the larger circle is twice as big as the smaller circle.
b) Find the ratio of areas of the red section to blue section.
Question 44
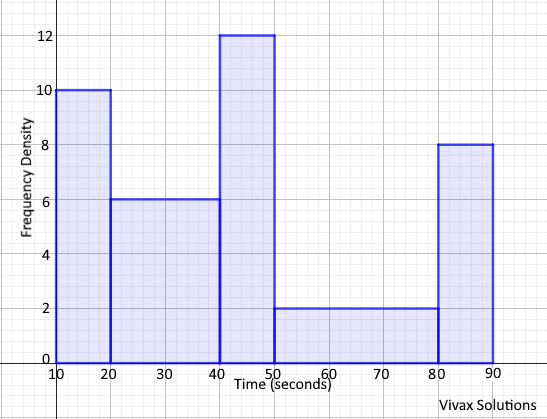
A large group of Year 11 students have been asked to learn the first 20 elements of the Periodic Table by heart. The above histogram shows frequency against the time taken by them.
There were 25 students who took between 10 to 20 seconds.
a) How do you justify the use of a histogram to represent the data?.
b) Find the total number of students.
c) What is the probability of a student taking between 60 to 70 seconds to remember the elements?
Question 45
Having mastered factorization for his GCSE, Ben showed the following to his friend, Piyal:
x = y
Multiply both sides by x,
x² = xy
Take away y²,
x² - y² = xy - y²
Factorizing both sides,
(x + y)(x - y) = y(x - y)
Dividing by (x - y)
x + y = y
Since x = y
2y = y
Dividing by y,
2 = 1! 😲
a) Piyal spotted the mistake. What was the mistake that Ben made?
b) Fully factorize 75x3 - 27xy².
c) Solve (2x - 3)² = 7, and leave the answer in surd form.
Question 46
Adrian thinks that n² + n + 41 is a prime number for any value of n. Jane does not agree with that.
a) How did Jane disprove Adrian's claim?
The first four terms of a linear sequence are as follows:
5, 11, 17, 23
b) Find the nth term of the sequence.
c) Prove that the difference of squares of any two consecutive terms of the sequence is a multiple of 12.
Question 47
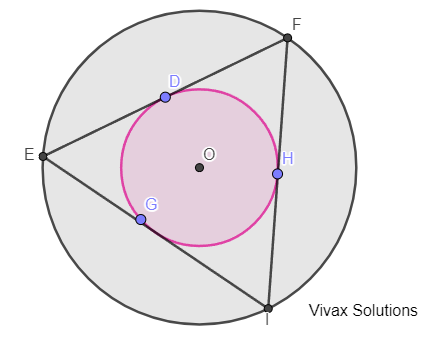
The two circles share the same centre, O and the radii are 2cm and 4cm respectively. Three longest lines drawn in the space between two circles are shown as above.
a) Show that EF, EI and FI are tangents to the smaller circle.
b) Find the total area between the larger circle and the triangle.
Question 48
Solve 3p + 3p-1 + 3p-2 = 39 and find p.
Question 49
A hedgehog that wants to cross a road of width, d, sees an owl on top of a tree of height 8m, on the other side of the road. The hedgehog sees the owl at an angle of elevation of 42°.
Then, it reluctantly crosses the road and looks at the owl again, to note the angle of elevation being 53°.
a) How wide is the road?
b) Find the distance between the tree and the edge of the road, closer to the tree.
Question 50
a) Sketch f(x) = (x + 1)/x and clearly mark the asymptotes, if any.
b) Sketch f(x) = -1/x on the same grid.
c) Solve algebraically or otherwise (x+1)/x + 1/x = 0 and comment on the feasibility of the answers.
Do you need detailed solutions to the above questions? Please click the following and you will be able to download a copy as a PDF:
Get Detailed Solutions
for All
Maths Questions
As a PDF
for Just £3.50
Question 51
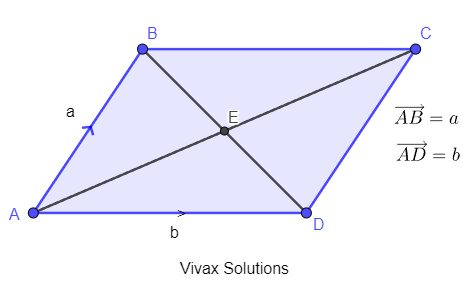
ABCD is a parallelogram and the two diagonals intersect at E.
a) Find vector expressions for both diagonals.
b) Hence prove that the two diagonals bisect each other.
Question 52
Move the points with your mouse or finger and you will see the sum of angles B and C remains 180°, regardless of the individual angles. If O is the centre of the circle, prove this fact geometrically - and algebraically - without using any of the circle theorems.
Question 53
Sarah runs the above spinner by clicking, Start Spin, button for some experiments with probability.
a) Find the probability of getting a 2.
b) Find the probability of getting a 2 or a 5.
c) If she spins twice, find the probability of getting a 2, followed by a 4.
d) If she spins twice, find the probability of getting a 3 and a 4 in any order.
e) If she spins twice, find the probability of getting a 5, at least once.
f) If she runs the spinner until she gets a 4 or total spins are two. Find the probability.
Question 54
There are n number of chocolates with a number written on them in a container; three of them have different prime numbers written on them. Fionna is allowed to take two chocolates, one chocolate at a time. If a prime number is written on a chocolate, she is allowed to eat it. If the probability of Fionna eating at least one chocolate with a prime number on it, is 4/5, find the value of n.
Question 55

The numbers, 3, 4 and 7, are written on three cards. They are arranged next to each other in such a way that they form a number less than 700.
a) Find the probability of getting two numbers with the last digit being 7.
b) Find the probability of the difference between the last two digits being odd.
Question 56
The probability of raining tomorrow is 0.6. If it rains, the probability of identical twins, Mrs Dorcey as well as Mrs Bayles, catching a cold is 0.4. Due to low immunity, even if it will not rain tomorrow, the probability of both women catching a cold is 0.2.
a) Find the probability of Mrs Dorcey catching a cold tomorrow.
b) Find the probability of neither of them catching a cold tomorrow.
Question 57
A number that cannot be written as a fraction is an irrational number. Surds are considered to be irrational numbers.
a) Find an irrational number between 5 and 6.
b) Daniel says that the product of two irrational numbers is always irrational. Giving an example, show that Daniel is not correct.
c) If a and b are integers, prove that (a + √b)(a - √b) is rational.
d) Show that 7√27/2√12 is rational.
Question 58
cos90 = cos60 x cos30 - sin30 x sin 60
The above is true for any three angles that follow the above pattern on both side of the equation.
a) Without using a calculator, find cos 75.
b) Without using a calculator, find cos 63 x cos 27 - sin 27 sin 63.
c) By using two appropriate angles, show that cos 120 < 0.
Question 59
There are 3 boys and 2 girls in a group.
a) How many ways can two boys and a girl be chosen for educational purposes?.
b) How many ways can two girls and a boy be chosen for an expedition?
Question 60
a) Solve 322x - 3y = 1/16 and 4x + y = 1, to find x and y.
b) Hence, find the value of z, if 8x x 4y = 2z.
Question 61
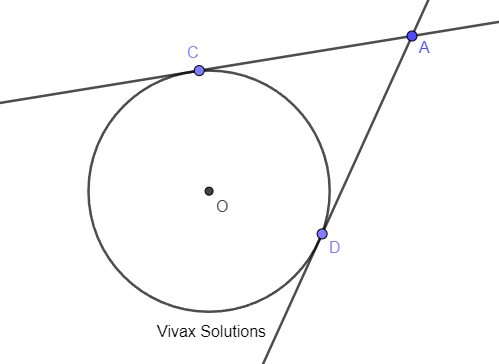
The radius of the circle is x and centre is O. CA and DA are two tangents to the circle. CA = x+7 and OA = x+8.
a) Find the value of x.
b) Find the angle between the two tangents.
c) Find the length of CD.
Question 62
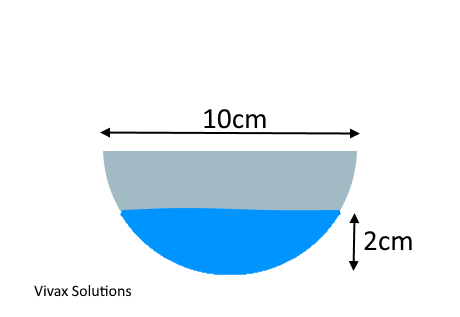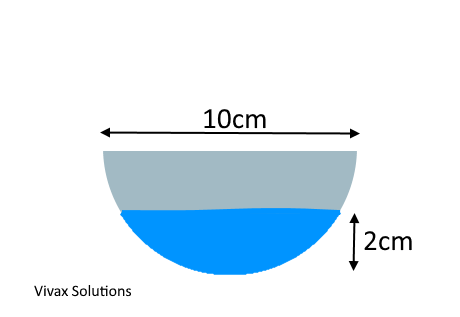
The above shows a cross section of a container that is a semicircle. The container is placed horizontally and filled with a liquid to a height, 2 cm. The length of the container is 10 cm.
a) Find the volume of the liquid in the container.
b) If the density of the liquid is 5000 kg/m3, find the mass of the liquid in the container in grams.
Question 63

There are 5 star chocolates, 3 round chocolates and a square chocolate in a container. Maya takes three chocolates from it.
a) Find the probability of equal number of star chocolates and round chocolates left in the container.
b) Find the probability of more round chocolates than star chocolates left in the container.
Question 64
xn+1 = xn(2 - 8x²n) is an iterative formula.
a) By using the calculator, find x1 to x10, if x0 = 0.02 .
b) Hence show that it is an approximate value of 1/√8.
c) Verify the answer to part, b), by rearranging the iterative formula.
Question 65
ABC is a triangle drawn inside a circle with AC being a diameter and O being the centre. BO is perpendicular to the diameter.
a) Show that cos 45° = 1/√2.
The point B is slightly moved so that the angle of BAC is equal to 53°.
b) If sin 53 = 5/8, find cos 37, without using a calculator.
c) Hence, find sin 37.
Question 66
The distance between two towns, A and B, is 600km. David drives his car at a steady speed of x km/h in the hope of arriving at B on time. Having traveled 3/4 of the distance, his car broke down unexpectedly. Within an hour, however, he rectified the problem and then, made it to town B on time, by just raising the speed by 25 km/h. Find the value of x.
Question 67
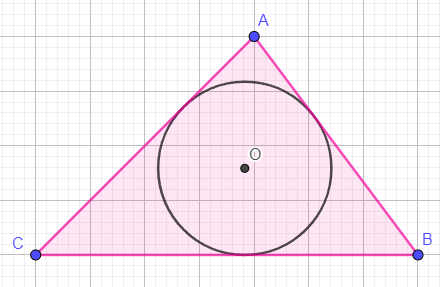
The perimeter of the inscribed circle is P and its radius is r. The area of the triangle is A. Prove that r = 2A/P.
Question 68
f(x) = x3 + 2x² - x - 2
a) Solve the above equation, f(x) = 0.
b) Sketch the curve, f(x).
c) Hence, sketch the curve f(2x) .
Question 69
x2 + (b/a)x + c/a = 0
a) Show that x = -b/2a ± √(b² - 4ac)/2a
b) Show that there will be no solution, if a = 2, c = 3 and b = 4
c) Hence, sketch the curve of the quadratic function and verify that there are no solutions.
Question 70
(x - p)(x - q) = x2 -4x - 5
a) Show that p + q = 4
b) Show that pq = -5
c) Find the value of 1/p + 1/q.
Question 71
The probability of getting a HEAD of a biased coin is 2/3. It is tossed up until a HEAD appears or the total number of tosses is equal to 3. Find the probability of getting at least 2 TAILs.
Question 72
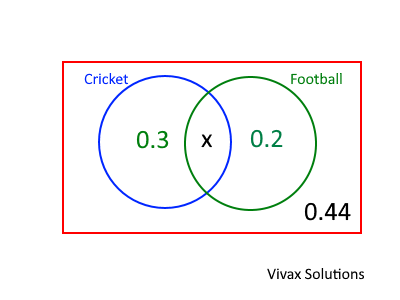
The boys in a certain group indicate how they like two type of sports, cricket and football.
a) Find the value of x.
b) Hence, determine whether the events, 'like cricket' and 'like football', are independent.
Question 73
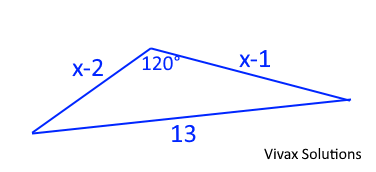
The lengths of the three sides of a triangle are shown above.
a) Find the value of x.
b) Hence, find the perimeter and area of the triangle.
Question 74
The product of the first and last of the four consecutive, positive integers is 154. Find the sum of the second and third integer.
Question 75
Factorize the following expression fully, stating in the form of linear expressions:
4x4 - 29x² + 25
Question 76
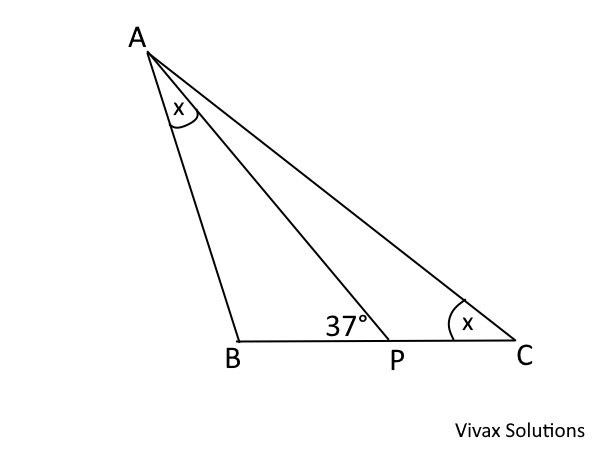
Show that AB/BP = AC/AP.
Question 77
There are two glasses, A and B, with diluted alcohol. The content in Glass A has 60% alcohol and that of Glass B has 30% alcohol. A certain volume from glass A and some volume from glass B are mixed together to form 120 ml of alcohol solution. Find the volumes taken from glass A and glass B to form the final solution that is 50% alcohol.
Question 78
A fruit picker is supposed to pluck a certain number of apples a day. Before midday, she picks 2/3 of her daily target. In the afternoon, she picks 2/5 of her remaining daily target and in the evening she picks the remaining 24kg of the target, in order to finish her daily task. What is her daily target in kg?
Question 79
ABCD is a trapezium with AD being parallel to BC and AD < BC. AB = 5 cm and the smallest distance between AD and BC is 4 cm. The two diagonals of the trapezium bisect the angles at B and C. Find the perimeter and area of the trapezium.
Question 80
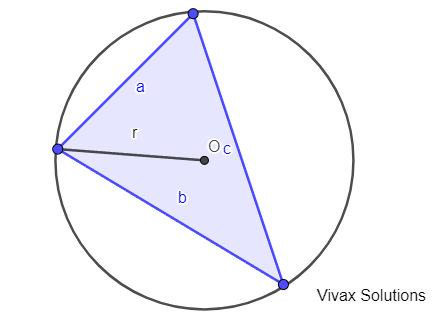
The lengths of the three sides of the triangle are a, b and c respectively. The area of the triangle is A and the radius is r. Prove that Ar : abc = 1 : 4.
Question 81
a) Show that n3 - n is a product of three consecutive numbers.
b) Hence show that it is a multiple of 3.
Question 82
A, B and C are three glasses filled with mixtures of alcohol and water. The alcohol contents of Glasses A, B and C are 30%, 20% and x%respectively. Three samples from each glass in the ratio of 12:5:3 are taken by volume and mixed together to form a mixture that contains 25% alcohol. Find the value of x.
Question 83
Solve 22x + 128 = (6)2x + 2 and find the possible values of x.
Question 84
If two digits are the same of a list of 2-digit integers, they are removed. Find the following probabilities:
a) Having a 4 in the units place.
b) Having a 4 in either tens place or units place.
Question 85
Let events A, and B such that P(A and B) = p; P(A' and B') = q.
a) If p > q, find p and q.
b) Hence find P(A or B).
Question 86
a) x = 0.47 + 0.47/100 + 0.47/10000 + 0.47/1000000 + ....
Show that the above value can be written as a fraction.
b) If S = x + 2x + 3x + .....+ nx, show that S = n(n + 1)x/2
Question 87
a) Solve x = 1 - 1/(2x - 5).
b) The two sides of a right-angled triangle are 2cm and 4cm shorter than its hypotenuse respectively. Find the area of the triangle.
Question 88
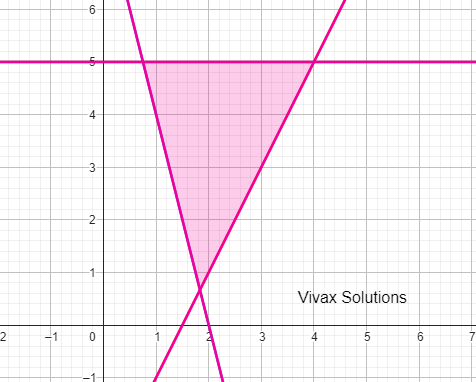
Write down three inequalities to represent the shaded region.
Question 89
When the length of a cube is decreased by 1cm, its volume goes down by 37cm3. If the length of the same cube is increased by 1 cm, its volume goes up by 61 cm3. Find the original volume of the cube. If the density of the cube is 80 g/cm3, find the masses of the three cubes.
Question 90
The distance, s, fallen by a stone, dropped from rest from a tall building, is given by the formula, s = 5t², where t is the time taken. During the last second of the fall, the stone moves through (16/25)th of the total height of the building. Find the height ofthe building and the total time taken for the fall.
Question 91
a) Show that (2n + 3)² - (2n - 3)² is a multiple of 12 for any value of n.
b) Simplify 5p/(p + q) - (2p - 3q)/(p - q) - (2p² - 6pq + 2q²)/(p² - q²)
Question 92
Two trains depart Birmingham Station at average speeds of 48 km/h and 60 km/h respectively towards Sheffield Station in the United Kingdom simultaneously. The first train reaches Sheffield station, 36 minutes after the second train arrives. Calculate the distance between the two cities.
Question 93
a) Solve x² - (m+n)x + mn = 0 and express the solutions in terms of m and n.
b) If the solutions of x² - 0.8x + 0.12 are p and q, without solving the equation, find the values of 1/p + 1/q and p² + q².
Question 94
a) Solve 2/(x² + 2) + 3/(x² + 3) = 2
b) The number of rows in a West End theatre equals the number of seats in each row. If we double the number of rows
and reduce the number of seats in a row by 10, then the number of seats in the theatre will increase by 300. How many rows are there in the cinema?
Question 95
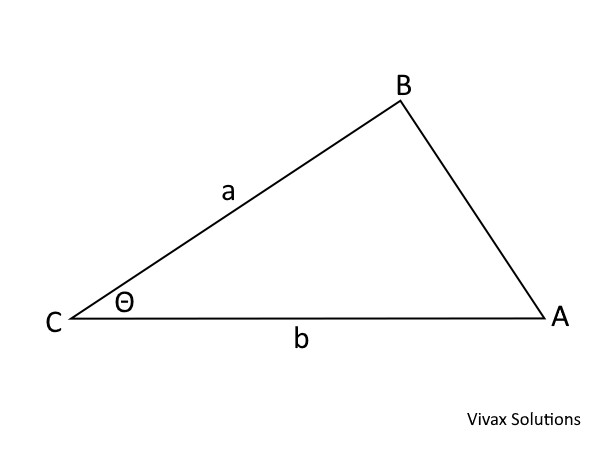
a) By drawing an appropriate line from B, prove that the area of the triangle = 1/2 ab sin Θ.
b) The ratio of hypotenuses of two right-angled triangles is 1 : 2. An acute angle of one triangle is 38° and that of the other is 52° respectively. If the area of the smaller triangle is 12 cm², find the area of the larger triangle.
Question 96
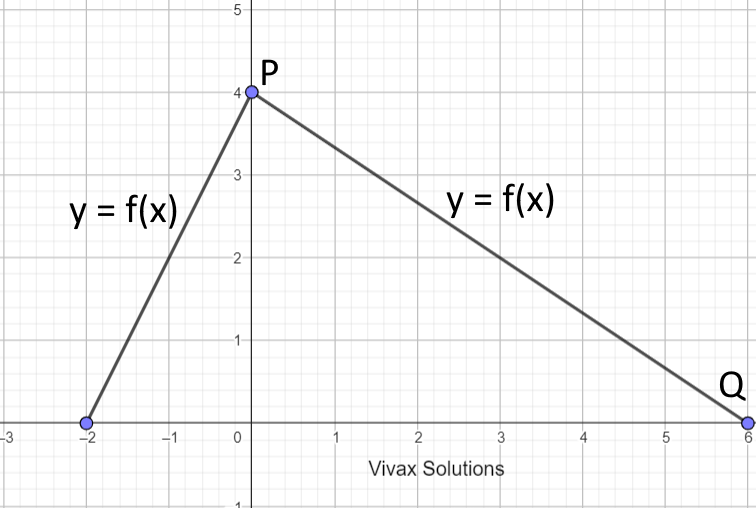
a) If f(x) = 2x - 3, find f²(x).
b) If f(x) = x²- 2x - 3, find f-1(x).
c) In the above diagram, find the value of ff(0).
Question 97
a) Show that n² + n + 3 is an odd number for any value of n.
b) If x² + 2px + q = 0, make x the subject of the equation.
c) Prove that x² - 6x + 12 ≥ 3 for all values of x.
Question 98
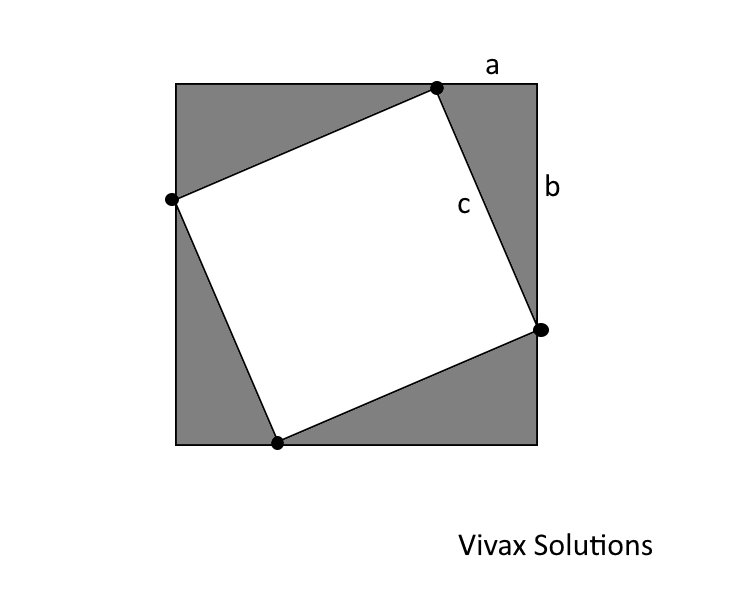
If the four right-angled triangles drawn in the square are congruent, derive Pythagoras Theorem from the above.
Question 99
David and Andrew live in London and Manchester respectively. The two major cities in England are 240 km apart. David and Andrew decided to meet up somewhere between the two cities at the weekend. They started driving leisurely at 60 km/h and 10 km/h respectively at 06:00.
a) Sketch a distance-time graph on the same grid to show the motion of the two drivers.
b) Find the distance travelled by David before meeting Andrew and the time taken for the journey.
Question 100
ABC is an equilateral triangle. The point P lies inside the triangle. The shortest distances from P to the three sides of the triangle are x, y and z. The perpendicular distance from any vertex to a side is l. Prove that l = x + y + z. Find the area of the triangle in terms of x, y and z.
Question 101
2y = √a x | x² = 1 - b²/4
Show that 4y = √(a(2-b)(2+b)).
Question 102
Sara says that there is a linear relationship between T and h in the equation, T = 2π√((H-h)/g). She wants to plot a graph of T² against h to obtain a straight line graph.
a) What is the gradient of the graph?
b) What is the y-intercept of the graph?
c) If the gradient and y-intercept are m and c respectively, show that H = c/m.
Question 103
a) Solve 2 - 7/√x = -3/x .
b) The product of two consecutive, positive even numbers is 41 more than the mean of the two numbers. Find the numbers.
Question 104
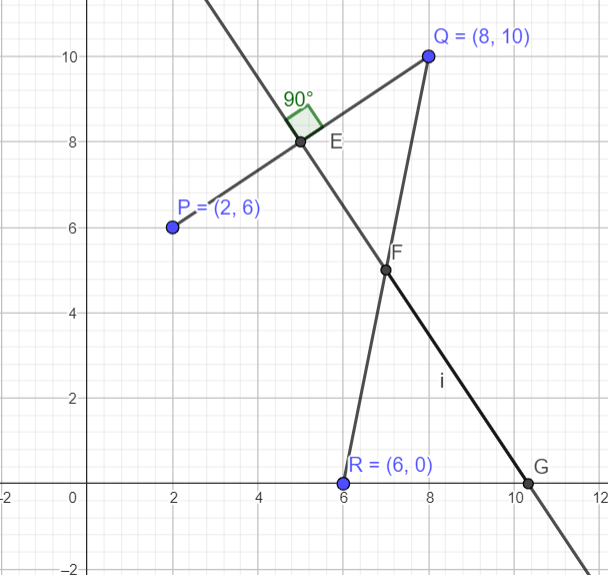
The point, E, is the mid-point of the line PQ. EFG is a straight line. The coordinates of P and Q are shown in the above diagram.
a) Find the equation of the line, EFG.
b) Find the coordinates of F and G.
c) Find the length FG.
Question 105
The numbers, 7,........,647, 651, form a linear sequence.
a) Find the nth term of the sequence.
b) How many terms are there in the sequence?
c) Is 438, a number of the sequence? Explain.
Question 106
Solve the following equation to find x and y.
9x² -32yx² + 32y+1 = 27
Question 107
There are a number of black and white balls in a container. The probability of picking a black ball is 3/8. The ball is put back into the container. Then, 2 more black balls and 7 white balls are added to the container. The new probability of picking a white ball is 2/9. How many black and white balls were originally in the container?
Question 108
The equation of an exponential curve is y = pqx. It passes through the points, (-2,12) and (3,0.375).
a) By sketching the curve, show that 0 < q < 1.
b) Find p, q and the y-intercept.
Question 109
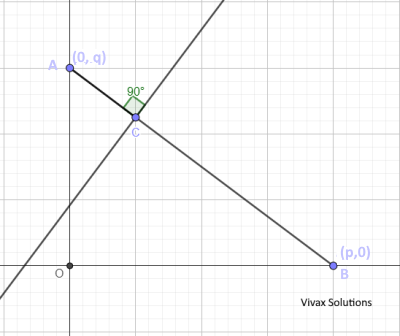
The straight line crosses the axes at (p, 0) and (0, q).
a) Show that the equation of the line is y/q + x/p = 1 .
The values o, p and q are 8 and 6 respectively. The point, C, lies on the line in such a way that AC = 1/4 of AB.
b) Find the coordinates of C.
c) Find the equation of the perpendicular line that goes through C.
Question 110
The function, f(x) = x² - x - 8 is defined on the interval, -4 ≤ x ≤ 2.
a) Find the greatest value of the function in the above range of x.
b) Find the lowest value of the function in the above range of x.
c) Find the distance between the two corresponding points on the curve.
Any comments? Please drop a line.
Do you need detailed solutions to the above questions? Please click the following and you will be able to download a copy as a PDF:
Get Detailed Solutions
for All the
Maths Questions
As a PDF
for Just £3.50
Answers: ↓ please move the mouse over the following space:
Q1: 1
Q2: 2x + 3y = 23; (4,5)
Q3: 47 | 11.81
Q4: 117.7°
Q5: 1/144 | 1 - (11/12)n
Q6: 3.6 | 12
Q7: 400 | 8
Q8: 7 | 18, 24, 42 | 6
Q9: 2, 1, -1 | x = -1 | (-1,-1) | 1 | -1.7, -0.3 | 1
Q10: 5/7
Q11: 75
Q13: 2, -3, 5
Q14: 5
Q15: 1600 | (x - 2)(x + 2)(x + 6)
Q16: 1/2 | 5
Q18: 144 | 84 | 30
Q19:10.4
Q20: 20 | 68.3
Q22: 12 : 15 : 10 | 12 : 20 : 105
Q23: ± √3 | 16, 9
Q24: 5
Q25: 5 | 43
Q26: 23.7 | 6
Q27: 3 | y ≥ 2x - 3; y ≥ 9 - x; y ≤ x + 3
Q28: 1
Q29: 406.87
Q31: 8
Q32: y = √(x+1) + 1
Q33: 1.5 | 3
Q34: 70.4°
Q35: 4.92 | 3.15
Q36: 5 | 2
Q37: 4 | -31/8
Q38: (3,3) | 12.4
Q39: x = 1.6 | y = 5.7
Q40: 18 | 1/9
Q41: 3 | 6
Q42: 3 : 1
Q43: 2(π-2)/(4-π)
Q44: 120 | 1/24
Q45: 3x(5x + 3y)(5x - 3y) | (3 ± √7)/2
Q46: 6n-1
Q47: 29.6
Q48: 3
Q49: 3, 6
Q50: -2
Q53: 1/8 | 3/8 | 5/128 | 5/64 | 7/16 | 135/256
Q54: 6
Q55: 1/2 | 1/2
Q56: 0.32 | 0.68
Q57: √31 | √2, √8
Q58: (√6 - √2)/4 | 0
Q59: 6 | 3
Q60: -4/25 | 4/25 | -4/25
Q61: 5 | 45.2 | 9.2
Q62: 112 | 560
Q63: 15/126 | 5/42
Q64: 60
Q65: 5/8 | √39/8
Q66: 50
Q68: -2 | 1 |-1
Q70: -0.8
Q71: 1/9
Q72: 0.06 | Not
Q73: 9 | 28 | 14√3
Q74: 25
Q75: (2x + 5)(x - 1)(x + 1)(2x - 5)
Q76:
Q77: 80 | 40
Q78: 120
Q79: 26 | 32
Q82: 131/3
Q83: x = 3 | x = 4
Q84: 8/81 | 17/81
Q85: 0.55, 0.05 | 0.95
Q86: 47/99
Q87: 2, 3/2 | 24
Q88: y ≥ 2x - 3 | y ≥ -4x+ 8 | y ≤ 5
Q89: 64 | 5120 | 2160 | 12,500
Q90: 31.25 | 2.5
Q91: Proof | (p + q) / (p - q)
Q92: 144 km
Q93: x = m, x = n | 20/3 | 0.4
Q94: x = 0 | 30 rows
Q95: 48
Q96: 4x - 9 | f-1(x) = 1 + √(x + 4) | 1.4
Q97: Proof
Q98: Proof
Q99: 180km | 6hrs
Q100: Proof
Q101: Proof
Q102: 4π²/g | 4π²H/g | proof
Q103: 1/4, 9 | 6, 8
Q104: y = -1.5x + 15.5 | (7,5), (10.3,0) | 6.01
Q105: 4n + 3 | 162 | No
Q106: ±√3, 1
Q107: 3, 5
Q108: Proof | 3, 1/2 | 3
Q109: Proof | 2,4.5 | 6y - 8x = 11
Q110: 12 | -5.61 | 18.64