Complex Numbers
In this comprehensive tutorial you will learn:
- The nature of a complex number
- Complex Conjugate
- Addition, subtraction, multiplication and division of complex numbers
- Finding complex roots of equations
- Argument and modulus of complex numbers
- Polar form of a complex number
- Locus of points on Argand Diagram
- Euler's relation - complex number in the exponential form
- de Moivre's Theorem
- Trigonometric Identities by de Moivre's Theorem
E.g.1
As with everything in maths, complex numbers
also have its own birth, may be even in multiple forms! This is one form of
it.
Suppose we want to solve the quadratic
equation, x2+ x + 6 = 0. If we
stick to the formula method, the process is as follows:
x = [-1 + √(1 - 24)]/2 or x
= [-1 - √(1 - 24)]/2
x = [-1 + √( - 23)]/2 or x
= [-1 - √(- 23)]/2
We cannot go beyond this point, as we
have come to a stage where we have a square root of a negative number; we have
been told it does not exist and we wind up our calculation with familiar
conclusions - there are no real roots or solutions. That's it.
However, that was not the end of the
world for mathematicians; they have gone much further than that and the concept
of complex numbers was born.
In the above example we came across
√(-23). Using the rules on indices, we can write it as follows:
√ -23 = √ -1 √ 23
Now we call √-1 as i, and suddenly √-23
becomes something that can be handled.
√-23 = i√ 23
Now, the above quadratic equation can be
solved!
x = (-1 + i√23)/2 or (-1 - i√23)/2
Solutions are expressed in terms of i.
These are called complex numbers.
Complex numbers are expressed in terms of
i or √-1.
- i = √-1
- i2 = √-1.√-1 = -1
- i3 =
√-1.√-1.√-1 = -i
- i4 =
√-1.√-1.√-1.√-1 = -1 x -1 = 1
The Form of a Complex Number
Z = a + ib
a = the real part of the complex number
ib = imaginary part of the complex number
i = √-1
A complex number can be
represented in a x-y grid. Then it is called an Argand Diagram: the real part is
shown in the x-axis and the imaginary part in the y-axis.
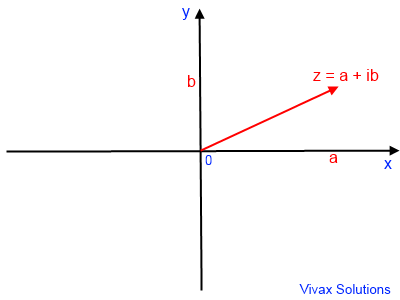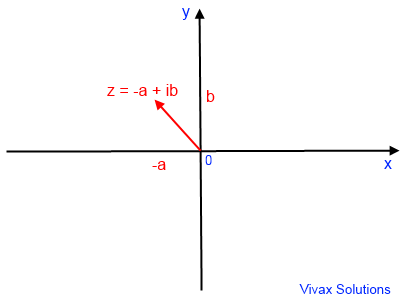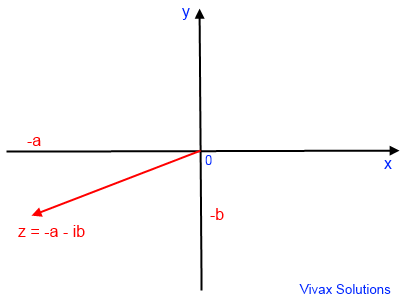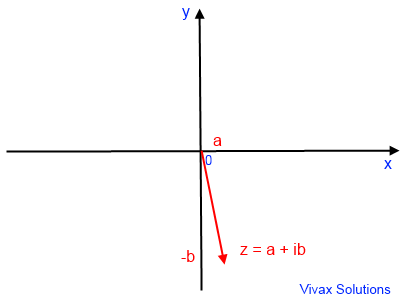
This is the Cartesian representation of a complex
number: the x-axis represents the real part; y-axis represents the imaginary part.
Complex numbers can be
added, subtracted, multiplied and even divided like any other number, with a bit
of caution though.
E.g.
Z1 = 8 + i6 ; Z2 = 2 - i4
Addition
Z1 +
Z2 = (8 + 2) + i (6 - 4) = 10 + i2
Subtraction
Z1 -
Z2 = (8 - 2) + i (6 - -4) = 6 + i10
You can practise addition and subtraction interactively with the following applet. Move Z1 and Z2 so that Z3 and Z4 represent addition and subtraction respectively.
Multiplication
Z1.Z2
= (8+i6).(2-i4)
= (8X2) - (8X4i) +
(2X6i) - 24i2
= 16 - i32 + i12 -
24(-1) ; note i2 = -1
= 16 -i20 +
24
= 40 - i20
Complex Conjugate - Z*
If a + bi is a complex number, a - bi is called its complex conjugate.
E.g.
Z = 2 - 3i, so Z* = 2 + 3i
Z = 2 + 3i, so Z* = 2 - 3i
Z = -2 - 3i, so Z* = -2 + 3i
Division
Z1 / Z2
= (8 + i6) / (2 - i4)
In this case, we need a special way of dealing with the division;
Multiply both the top
and the bottom by the complex conjugate of the bottom. That's it.
Z1 / Z2
= (8 + i6) * (2 + i4) / [(2 - i4)(2 + i4)]
= (16 + i32 + i12
+ i224) / (4 + i8 - i8 - i216)
= (-8 + i44) /
(20)
= -2/5 +
i(11/5)
You can practise multiplication and division interactively with the following applet. Move Z1 and Z2 so that Z3 and Z4 represent multiplication and division respectively.
Finding the square root of a complex number
Find the square root of 8 + 6i
Let (a + bi)2 = 8 + 6i, where a + bi is the square root of 8 + 6i.
So, a2 + 2abi - b2 = 8 + 6i
Making the real parts on both sides equal,
a2 - b2 = 8
Making the coefficients of i on both sides equal,
2ab = 6 => b = 6/2a = 3/a
Sub in the other,
a2 - 9/a2 = 8
a4 - 9 = 8a2
a4 -8a2 -9 = 0
Let y = a2
So, y2 -8y -9 = 0
(y - 9)(y + 1)
y = 9 or y = -1 => a2 = 9 or a2 = -1
Since a2 = -1 not valid, a2 = 9 => a = ± 3
Sub in b = 3/a => b = 1 or b = -1
So, the square roots of 8 + 6i = (3 + i) or (-3 -i)
The modulus of a complex number - |Z|
The length of the vector that represents the complex number is called its modulus.
If z = a + ib, then modulus is defined as,
√(a2 + b2)
|Z| =√(a2 + b2)
The argument of a complex number - arg z
The angle between the positive real axis and the vector that represents the complex number is the argument of the complex number.
If arg z = θ, -180 < θ <= 180 or -π < θ <= π
You can practise the concepts with the following animation. Please move the point, Z1 with your mouse and see the changes.
Have you noticed how the arg z, changes? It can only take values between -1800 and 1800 - or its radian equivalents.
Solving Polynomial Equations
If a polynomial equation - quadratic or higher - has complex roots, they are in the form of conjugate pairs - a ± b. Sometimes, one or many be real roots as well - a ±0i.
E.g.1
Solve x3 - 6x2 + 21x - 26 = 0
f(x) = 0
f(2) = 0 => from factor theorem, x-2 is a factor.
Divide x3 - 6x2 + 21x - 26 by (x-2)
You get, x2 - 14x + 13 with no remainder.
Solve, x2 - 14x + 13 = 0
x = 2 ± 3i
So, the roots are x =2, x = 2 ± 3i
You can see that there is one real root and two complex roots for the equation - in complex conjugate form.
You can use the following applet to solve polynomials. Just type in the equation in the text box and click the button. Make sure you use, ^, to represent the powers of x. Use arrow keys, rather than the mouse, while typing in the equations. All roots appear with, Z. If they are not visible, just move the grid and look for them!
The Locus of points on an Argand Diagram
Complex numbers can be used to find the locus of points on an Argand diagram.
E.g.1
The locus of a point, Z, which keeps the distance between it and a fixed point, Z1 , the same is a circle.
In the example, |Z - Z1| = 3; it means the locus of the point in question is a circle of radius 3, with the centre at Z1.
In order to animate it and see it in action, please press the play button.
|Z - Z1| = 3
|Z - (5 + 4i)| = 3
|Z - 5 - 4i)| = 3
This is a circle with centre, (5,4) and radius = 3.
So, the equation of the locus - the circle in this case - is (x - 5)2 + (y - 4)2 = 32.
E.g.2
The locus of a point, Z, which keeps the distance between two fixed points, Z1 and Z2, the same is the perpendicular bisector of the line between the two points.
In the example, the point, Z, moves while keeping the distances between the points, Z1 and Z2, the same; it means the locus of the point in question is the perpendicular bisector of the line that joins Z1 and Z2.
In order to animate it and see it in action, please press the play button.
You can move the point, Z, in order to see that it lies on the perpendicular bisector.
Since it is a straight line, the equation of the locus takes y = mx + c form.
Please move the point, Z1, to see how the equation of the locus changes. You can use it as an exercise to find the equation of the locus.
The polar representation of a complex number - modulus argument form
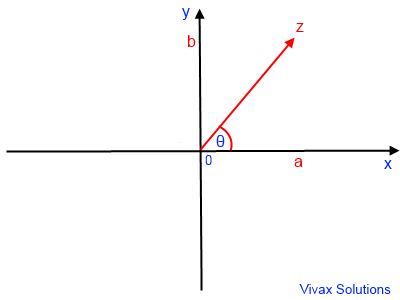
Here, the angle t in radians is called the argument. Therefore, the complex number can be written in
terms of its modulus and the argument. This is called the polar
representation of the complex number
a = |Z| cos θ : b = |Z| sin t : θ = tan
-1(b/a) ; -π< θ <= π
Z = |Z| cos θ + i|Z| sin θ
If the modulus of a complex number is r and the
argument is t, it can be written as (r,θ) in the polar form.
E.g.1
Write the complex number, Z = 3 + i4
in the polar form.
|Z| = √(32 + 42) = 5
t = tan
-1(4/3) = 0.92
Z = (5,0.92).
E.g.2
Write Z = (10,0.3) in Cartesian
form.
a = 10 cos 0.3 = 9.5
b= 10 sin 0.3 = 2.9
Z = 9.5 + i2.9
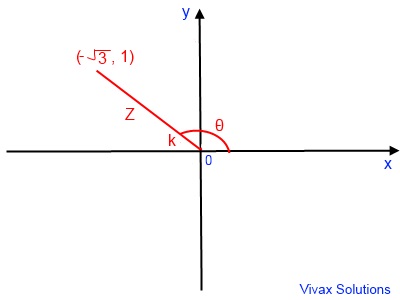
E.g.3
If Z = -√3 + i, write it in the form of r(cos θ + i sin θ).
tan k = 1/√3
k = π/6
θ = π - k = 5π/6
|Z| = √(3 + 1) = 2
Z = 2(cos 5π/6 + i sin 5π/6)
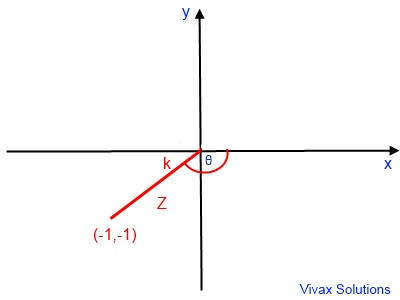
E.g.4
If Z = -1 - i, write it in the form of r(cos θ + i sin θ).
tan k = -1/-1 = 1
k = π/4
θ = π + k or -(π - k);
Since -π< θ <=π
θ = -(π - π/4) = -3π/4
|Z| = √(1 + 1) = √2
Z = √2(cos -3π/4 + i sin -3π/4)
Maclaurin Series
f(x) = f(0) + f'(0)x/1! + f"(0)x2/2! + f"'(0)x3/3! + ....
sin(x) = sin(0) + cos(0)x/1! + -sin(0)x2/2! - cos(0)x3/3! + ...
= x -x3/3! + x5/5!
cos(x) = cos(0) - sin(0)x/1! - cos(0)x2/2! + sin(0)x3/3! + ...
= 1 -x2/3! + x4/4!
ex = 1 + e0x/1! + e0x2/2! + e0x3x/3!+...
= 1 + x + x2/2! + x3/3! + ...
Complex Numbers in Exponential Forms - Euler's Relation
From Maclaurin Series,
eiθ = 1 + iθ/1! + (iθ)2/2! + (iθ)3/3! + ...
= 1 + iθ - θ2 -iθ3/3! + θ4/4! + iθ5/5! - θ6/6!
= (1 - θ2 + θ4/4! - θ6/6!... ) + i(iθ -iθ3/3! + iθ5/5!...)
= cos θ + i sin θ
eiθ = cos θ + i sin θ
Z = r[cos θ + i sin θ ]
Z= reiθ
E.g.1
Express Z = √3 + i in the form of Z = reiθ
r = √(3 + 1) = 2
tan θ = 1/√3 => θ = π/6
Z = eiπ/6
E.g.2
Express Z = 3 cos π/3 + i sin π/3 in the form of Z = eiθ.
r = 3; θ=π/3
Z = 3eiπ/3
E.g.3
Express Z = 5 cos π/4 - i sin π/4 in the form of Z = eiθ.
Z = 5 cos (-π/4) + i sin (-π/4), because cos(-x) = cos(x) and sin(-x) = -sin(x)
r = 3; and θ=-π/4
Z = 3e-iπ/4
E.g.4
Express Z = 4ei5π/4 in the form of Z = r[cos θ + i sinθ].
Since -π< θ <=π, θ = -π/4; r = 4
So, Z = 2[cos -π/4 + i sin -π/4]
E.g.5
Use Euler's relation to verify that cos²Θ + sin²Θ ≡ 1.
eiθ = cosθ + i sinθ
e-iθ = cos(-θ) + i sin(-θ) = cosθ − i sinθ
Multiplying the two equations gives
1 = eiθ × e-iθ = (cosθ + i sinθ)(cosθ − i sinθ)
= cos2 θ + sin2 θ
Product and Division of Complex Numbers
Let Z1 = r1[cosθ1; + i sinθ1;] = eiθ1; ;
Z2 = r2[cosθ2; + i sinθ2;] = eiθ2;
Method 1
|Z1Z2| = |Z1||Z2| and arg(Z1Z2) = arg(Z1) + arg(Z2)
Given Complex Numbers in Polar Form
Let Z1 and Z2 be two complex numbers in polar form:
Z1 = r1 (cos Θ1 + i sin Θ1)
Z2 = r2 (cos Θ2 + i sin Θ2)
Where r1 = |Z1| and r2 = |Z2| are the moduli (magnitudes), and Θ1 and Θ2 are the arguments (angles).
The product of the individual moduli is:
|Z1| |Z2| = r1 r2
Find the Product Z1 Z2
Multiply Z1 and Z2:
Z1 Z2 = [r1 (cos Θ1 + i sin Θ1)] [r2 (cos Θ2 + i sin Θ2)]
Z1 Z2 = r1 r2 [(cos Θ1 cos Θ2) + i (cos Θ1 sin Θ2) + i (sin Θ1 cos Θ2) + i^2 (sin Θ1 sin Θ2)]
Since i2= -1, we group the real and imaginary parts:
Z1 Z2 = r1 r2 [ (cos Θ1 cos Θ2 - sin Θ1 sin Θ2) + i (cos Θ1 sin Θ2 + sin Θ1 cos Θ2) ]
Apply Trigonometric Addition Formulas
We use the trigonometric identities:
cos(A + B) = cos A cos B - sin A sin B
sin(A + B) = sin A cos B + cos A sin B
Applying these to the product (where A = Θ1 and B = Θ2):
Z1 Z2 = r1 r2 [ cos(Θ1 + Θ2) + i sin(Θ1 + Θ2) ]
Find the Modulus of the Product |Z1 Z2|
|Z1 Z2| = r1 r2
arg(Z1 Z2) = arg(Z1) + arg(Z2)
Method 2
Z1 X Z2 = r1eiθ2; X r2eiθ2;
= r1r2ei[θ1 + θ2]
= r1r2[cos(θ1 + θ1) + i sin(θ1 + θ2)]
The division of the individual moduli is:
Method 1
|Z1| / |Z2| = r1 / r2
Divide Z1 and Z2:
Z1 / Z2 = [r1 (cos Θ1 + i sin Θ1)] / [r2 (cos Θ2 + i sin Θ2)]
To simplify, we multiply the numerator and denominator by the conjugate of the denominator, (cos Θ2 - i sin Θ2):
Z1 / Z2 = (r1 / r2) * [(cos Θ1 + i sin Θ1)(cos Θ2 - i sin Θ2)] / [(cos Θ2 + i sin Θ2)(cos Θ2 - i sin Θ2)]
The denominator simplifies to cos² Θ2 + sin² Θ2 = 1.
The numerator expands as:
cos Θ1 cos Θ2 - i cos Θ1 sin Θ2 + i sin Θ1 cos Θ2 - i² sin Θ1 sin Θ2
Since i²= -1, we group the real and imaginary parts:
Z1 / Z2 = r1 / r2 [ (cos Θ1 cos Θ2 + sin Θ1 sin Θ2) + i (sin Θ1 cos Θ2 - cos Θ1 sin Θ2) ]
Apply Trigonometric Subtraction Formulas:
We use the trigonometric identities:
cos(A - B) = cos A cos B + sin A sin B
sin(A - B) = sin A cos B - cos A sin B
Applying these to the division (where A = Θ1 and B = Θ2):
Z1 / Z2 = r1 / r2 [ cos(Θ1 - Θ2) + i sin(Θ1 - Θ2) ]
Find the Modulus of the Quotient |Z1 / Z2|
|Z1 / Z2| = r1 / r2
arg(Z1 / Z2) = arg(Z1) - arg(Z2)
Method 2
Z1 / Z2 = r1eiθ2; / r2eiθ2;
= (r1/r2) ei[θ1 - θ2]
= (r1/r2) [cos(θ1 - θ1) + i sin(θ1 - θ2)]
Based on the above proofs, the following set of rules applies in dealing with the product and division of complex numbers:
|Z1 Z2 | = |Z1||Z1|
arg(Z1Z2) = arg(Z1) + arg(Z2)
|Z1 / Z2 | = |Z1|/|Z1|
arg(Z1 / Z2) = arg(Z1) - arg(Z2)
E.g.1
Express 2(cosπ/6 + i sinπ/6) X 3(cosπ/6 + i sinπ/6)in the form of x + iy.
= 6(cos(π/6+π/6) + i sin(π/6+π/6)
= 6(cosπ/3 + i sinπ/3)
= 3 + 3√3i
E.g.2
Express 12(cos5π/6 + i sin5π/6) / 3(cos2π/6 + i sin2π/6)in the form of x + iy.
= 4(cos(5π/6-2π/6) + i sin(5π/6-2π/6)
= 4(cos3π/6 + i sin3π/6)
= 4(cosπ/2 + i sinπ/2)
= 4(0 + i)
= 4i
E.g.3
Express 5(cos5π/6 + i sin5π/6) X 2(cos2π/6 - i sin2π/6)in the form of x + iy.
= 5(cos5π/6 + i sin5π/6) X 2(cos(-2π/6) + i sin(-2π/6)) , because, cos-θ = cosθ and sin-θ = -sinθ
= 10(cos3π/6 + i sin3π/6)
= 10(cosπ/2 + i sinπ/2)
= 10(0 + 1i)
= 10i
de Moivre's Theorem
[r(cosθ + isinθ)]n = rn[cos nθ + i sin nθ]
de Moivre Theorem in exponential form
Z = r[cosθ + isinθ]
Z
n = r
n[cosθ + isinθ]
n
Z
n = r
n[cos nθ + isin nθ]
Z
n = r
ne
i(nθ)
The path leading to de Moivre's Theorem
By multiplying two complex numbers together, it is easy to show the path that leads to de Moivre Theorem, which is as follows:
Z = r[cosθ + i sinθ]
Z
1 = r
1[cos1θ + i sin1θ]
1
Z
2 = Z X Z = r
2[cos2θ + i sin2θ]
2
Z
3 = Z
2 X Z = r
2[cos2θ + i sin2θ] X [cos1θ + i sin1θ]
Z
3 = r
3[cos3θ + i sin3θ]
3
Z
4 = Z
3 X Z = r
3[cos3θ + i sin3θ] X [cos1θ + i sin1θ]
Z
4 = r
4[cos4θ + i sin4θ]
4
Z
5 = Z
4 X Z = r
4[cos4θ + i sin4θ] X [cos1θ + i sin1θ]
Z
5 = r
5[cos5θ + i sin5θ]
5
...
...
...
...
Z
n = r
n[cos nθ + i sin nθ]
n
This is
de Moivre's Theorem.
de Moivre's Theorem is valid for any rational number - negative and positive integers as well as fractions. Normally, it is proved by the mathematical induction method.
It is true for any positive integer, n
[r(cos θ + i sinθ)]
n = r
n[cos nθ + i sin nθ]
n=1
LHS: [r(cos θ + i sinθ)]
1 = r[cosθ + i sinθ]
RHS: r
1[(cos1θ + i sin1θ)] = r[cosθ + i sinθ]
Since
LHS: =
RHS:, de Moivre Theorem is true for n=1.
Assume that de Moivre's Theorme is true for
n=k. So,
Z
k = r
k[cos kθ + i sin kθ]
Now. let's try it for n = k+1
[r(cos θ + i sinθ)]
k+1 = [r(cosθ + i sinθ)]
k[r(cos θ + i sin θ)]
= [r
k(cos kθ + i sin kθ)][r(cosθ + i sinθ)]
= [r
k+1(cos (k+1)θ + i sin (k+1)θ)]
Therefore, if de Moivre's Theorem is true for n=k, it is true for n=k+1; Since it is true for n=1 too, de Moivre's Theorem is true for any integer, n>=1.
n=0
LHS: [r(cos θ + i sinθ)]0 = 1
RHS: r0[(cos0θ + i sin 0θ)] = 1[1 + 0] = 1
Since LHS: = RHS:, de Moivre's Theorem is true when n=0.
n is negative => n<0
Let n=-m, where m is a positive number.
Since the theorem is true for positive integers,
LHS: [r(cos θ + i sinθ)]n = [r(cos θ + i sinθ)]-m
= 1 / [r(cos θ + i sinθ)]m
= 1 / [r(cos mθ + i msinθ)] (since it is valid for positive integers)
X [cos mθ - i sin mθ] / [cos mθ - i sin mθ] =>
= [cos mθ - i sin mθ] / [(cos mθ - i sin mθ)rm(cos mθ + i msinθ)] =>
= [cos mθ - i sin mθ] / rm[cos2mθ - i2 sin 2mθ]
= [cos mθ - i sin mθ] / rm[cos2mθ + sin 2mθ]
= [cos mθ - i sin mθ] / rm X 1
=r-m[cos mθ - i sin mθ]
=r-m[cos (-mθ) + i sin (-mθ)], since cos-θ= cosθ and sin-θ=-sinθ
Since -m = n
rn[cos nθ) + i sin nθ]
RHS:
For fractions
Let n=p/q, where p and q are integers.
[r(cos θ + i sinθ)]
p = r
p[cos pθ + i sin pθ]
= r
p[cos pq(1/q)θ + i sin pq(1/q)θ]
= r
p[cos p(1/q)θ + i sin p(1/q)θ]
q
Now take the q
th root of both sides
=r
p/q[cos p(1/q)θ + i sin p(1/q)θ]
=r
p/q[cos (p/q)θ + i sin (p/q)θ]
= r
n[cos nθ + i sin nθ]
Therefore, deMoivre's Theorem is valid for fractions as well.
Using de Moivre's Theorem
E.g.1
Find the value of (1 − √3 i)6
If z = 1 − √3 i, then
r = √(12 + (−√3)2) = √(1 + 3) = √4 = 2
θ = arg z = −tan−1(√3/1) = −π/3
So, 1 − √3 i = 2 [ cos(−π/3) + i sin(−π/3) ]
∴ (1 − √3 i)6 = [ 2 ( cos(−π/3) + i sin(−π/3) ) ]6
= (2)6 ( cos(−6π/3) + i sin(−6π/3) )
= 64(cos(−2π) + i sin(−2π))
= 64(1 + i(0))
= 64
E.g.2
Express the numerator and denominator using Euler's formula, eiθ = cosθ + i sinθ.
cos 5θ + i sin 5θ = ei 5θ
(cos 2θ + i sin 2θ)2 = (ei 2θ)2
Now substitute these back into the fraction:
a cos 5θ + i sin 5θ
—————————
(cos 2θ + i sin 2θ)2
= ei 5θ
——————
(ei 2θ)2
Apply the exponent rule (am)n = amn to the denominator:
= ei 5θ
——————
ei 4θ
Apply the exponent rule am / an = am−n:
= ei 5θ − i 4θ
= ei (5−4)θ
= eiθ
Sum of Complex Numbers and Reciprocals
Z = (cos Θ + i sin Θ)
Z-1 = (cos Θ + isin Θ)-1
= cos(-Θ) + isin(-Θ) - from de Moivre's Theorem
= cos Θ - sin Θ
Z + 1/Z = (cos Θ + i sin Θ) + (cos Θ - i sin Θ) = 2cos Θ
Z - 1/Z = (cos Θ + i sin Θ) - (cos Θ - i sin Θ) = 2isin Θ
Z = (cos Θ + i sin Θ)
Zn = (cos Θ + i sin Θ)n = (cos nΘ + i sin nΘ) - from de Moivre's Theorem
Z-n = (cos Θ + isin Θ)-n = (cos nΘ - i sin nΘ) - from de Moivre's Theorem
Zn + 1/Zn = (cos nΘ + i sin nΘ) + (cos nΘ - i sin nΘ) = 2cos nΘ
Zn - 1/Zn = (cos nΘ + i sin nΘ) - (cos nΘ - i sin nΘ) = 2isin nΘ
Derivation of Trigonometric Identities by de Moivre's Theorem
In order to derive the trigonometric identities, we are going to use the binomial expansion along with de Moivre Theorem.
(a + x)n = Σ nCr an-r xr
E.g.1
Find an identity for cos5θ.
[cosθ + i sinθ]5 = Σ 5Cr cosθ5-r (i sinθ)r
= cos5θ + 5 cos4θ(i sinθ) + 10 cos3θ(i sinθ)2 + 10 cos2θ(i sinθ)3 + 5 cosθ(i sinθ)4 + (i sinθ)5
= cos5θ + 5 cos4θ(i sinθ) + 10 cos3θ(-sin2θ) + 10 cos2θ(-i sin3θ) + 5 cosθ(sin4θ) + (i sin5θ)
From de Moivre't Theorem,
[cosθ + sinθ]5 = [cos5θ + i sin5θ]
So, [cos5θ + i sin5θ] = cos5θ + 5 cos4θ(i sinθ) + 10 cos3θ(-sin2θ) + 10 cos2θ(-i sin3θ) + 5 cosθ(sin4θ) + (i sin5θ)
Now equate the real parts on both sides:
cos5θ = cos5θ + 10 cos3θ(-sin2θ) + 5 cosθsin4θ
= cos5θ + 10 cos3θ(-sin2θ) + 5 cosθ(sin2θ)2
= cos5θ -10 cos3θsin2θ + 5 cosθ(1 - cos2θ)2
= cos5θ -10 cos3θ(1 - cos2θ) + 5 cosθ(1 -2cos2θ + cos4θ)
= cos5θ -10 cos3θ + 10 cos5θ + 5 cosθ -10cos3θ +5cos5θ
= 16cos5θ -20 cos3θ + 5 cosθ
cos 5θ = 16cos5θ -20 cos3θ + 5 cosθ
E.g.2
Find an identity for sin4θ.
[cosθ + i sinθ]4 = Σ 4Cr cosθ4-r (i sinθ)r
= cos4θ + 4 cos3θ(i sinθ) + 6 cos2θ(i sinθ)2 + 4 cosθ(i sinθ)3 + (i sinθ)4
= cos4θ + 4 cos3θ(i sinθ) + 6 cos2θ(-sin2θ) + 4 cosθ(-i sin3θ) + (i sin4θ)
From de Moivre't Theorem,
[cosθ + sinθ]4 = [cos4θ + i sin4θ]
So, [cos4θ + i sin4θ] = = cos4θ + 4 cos3θ(i sinθ) + 6 cos2θ(-sin2θ) + 4 cosθ(-i sin3θ) + (i sin4θ)
Now equate the imaginary parts on both sides:
sin4θ = 4cos3θsinθ - 4 cosθ sin3θ + sin4θ
sin 4θ = 4cos3θsinθ - 4 cosθ sin3θ + sin4θ
E.g.3
Find an identity for cos²θ.
Z2 + 1/Z2 = 2 cos 2Θ → 1)
(cos Θ + isin Θ)² + (cos Θ - isin Θ)² = (cos²Θ + 2cos Θisin Θ -sin²Θ) + (cos²Θ - 2cos Θisin Θ - sin²Θ) = 2 cos²Θ _ 2sin²Θ → 2)
From 1) and 2)
2 cos2Θ = 2 cos²Θ - 2 sin²Θ
cos2Θ = cos²Θ - sin²Θ
Since cos²Θ + sin²Θ = 1 → sin²Θ = 1 - cos²Θ
cos 2Θ = 2cos²Θ - 1
cos²Θ = (1 + cos2Θ)/2
E.g.4
Find an expression for cos4Θ in terms of cos 4Θ and cos 2Θ.
(Z + 1/Z)4 = (2 cos Θ)4 = 16cos4Θ → 1)
Using binomial theorem,
(Z + 1/Z)4 =Z4 + 4Z31/Z + 6Z21/Z2 + 4Z 1/Z3 + 1/Z4
= (Z4 + 1/Z4) + 4(Z2 + 1/Z2) + 6
= 2 cos 4Θ + 4 cos 2Θ + 6 → 2)
1) = 2)
16cos4Θ = 2 cos 4Θ + 8 cos 2Θ + 6
cos4Θ = 2/16 cos 4Θ + 8/16 cos 2Θ + 6/16
cos4Θ = 1/8 cos 4Θ + 4/8 cos 2Θ + 3/8
cos4Θ = 1/8[cos 4Θ + 4 cos 2Θ + 3]