Circle Theorems
There are eight circle theorems. They are as follows:
- Circle Theorem 1: The angle subtended by a chord at the centre is twice the size of the angle subtended by the same chord at the circumference.
- Circle Theorem 2: The angles subtended by a chord in the same segment are equal.
- Circle Theorem 3: The angle of a semi-circle is a right angle.
- Circle Theorem 4: The opposite angles of a cyclic quadrilateral add up to 1800.
- Circle Theorem 5: The angle between a tangent and a radius at the point of contact is a right angle.
- Circle Theorem 6: The two tangents drawn to a circle from a point are equal in length.
- Circle Theorem 7: The angle between a chord and a tangent is equal to the angle subtended by the same chord in the alternate segment.
- Circle Theorem 8: The perpendicular line from the centre to a chord, bisects it.
The following image shows the basics of a circle; they are really important to learn the circle theorems.
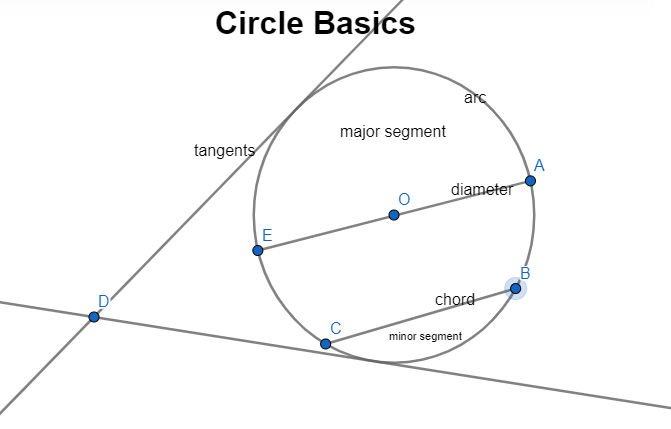
You can practise the seven circle theorems with the following simulations; just move the point/s on the circumference and see how they work for yourself. It's fun!
AS and A Level Only
Circle Theorems - proof
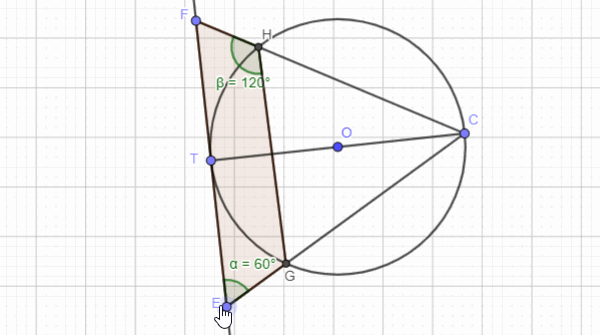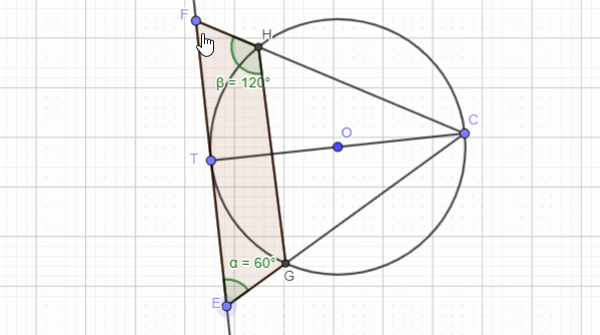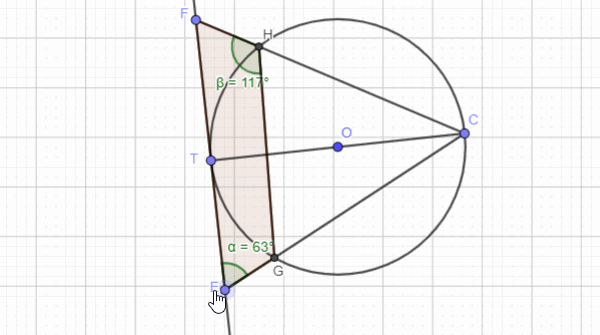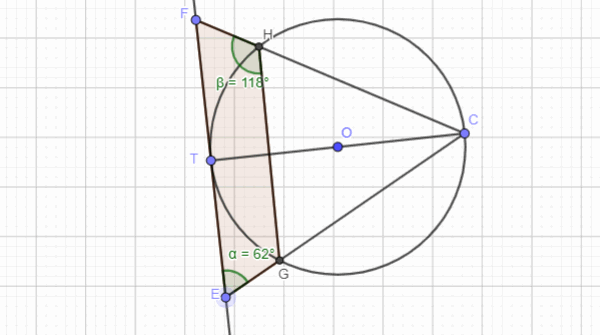
The following images show how circle theorems can be proven from basic geometry. Most examination boards in England want students to learn the proofs along with the theorems.
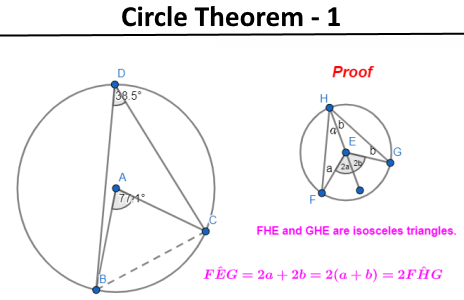
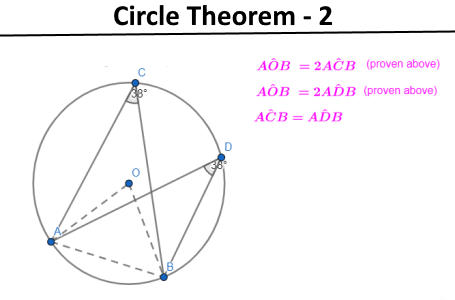
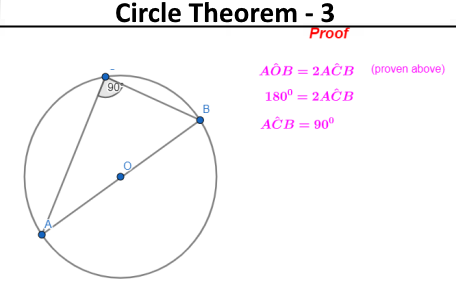
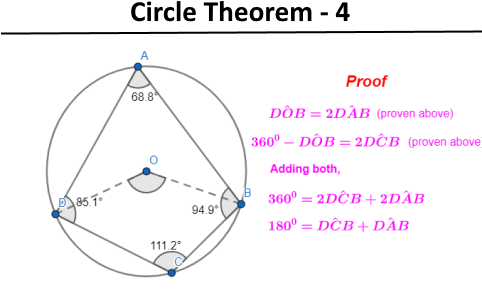
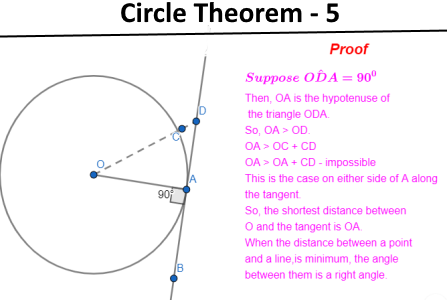
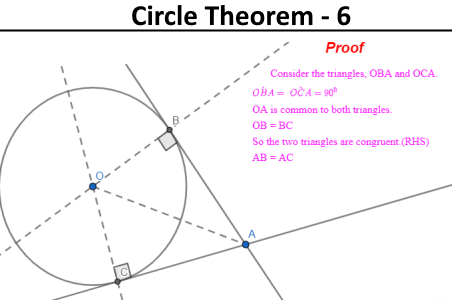
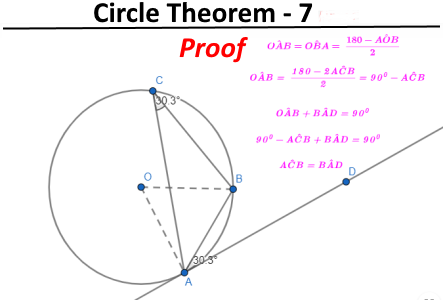
Problem Solving - circle theorems
E.g.1
If BC = CD and ∠DCF = 270 Find ∠BAC and ∠BCE.
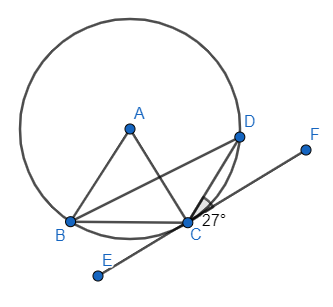
∠CBD = 270 (alternate segment theorem)
∠BDC = 270 (isosceles triangle)
∠BAC = 540 (angle subtended by a chord at the centre = 2 x angle subtended by a chord at the circumference)
∠BAD = 180 -54 = 1260 (angle of a triangle add up to 1800)
∠BCE = 180 -(126+27) = 27 (angles on a straight line add up to 1800)
E.g.2
If BA = x, AC = (x - 3), AD = 3cm and EA = 6cm Find x.
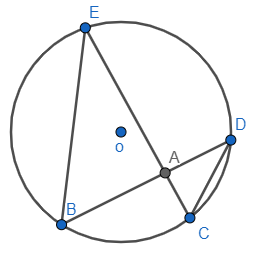
∠BEA = ∠ADC (angles subtended in the same segment)
∠EBA = ∠ACD (angles subtended in the same segment)
∠EAB = ∠DAC (vertically opposite angle)
So, EAB and DAC triangles are similar.
BA/AD = EA/AC (corresponding sides are in the same ratio)
x(x - 3) = 6 x 3
x2 - 3x - 18 = 0
x = 6 or x = 3.
x = 6cm.
E.g.3
Show that BE is parallel to CO.
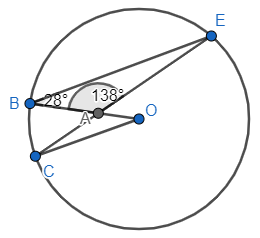
∠BEC = 180 - (28 + 138) = 140 (angles of a triangle)
∠BOC = 280 (angles subtended by a chord at the centre is twice that of the same at the circumference)
∠CAO = ∠BAE (vertically opposite angle)
∠ACO = 180 - (28 + 138) = 140 (angles of a triangle)
∠BEA = ∠ACO and ∠ABE = ∠AOC (appear to be alternate angles)
So, BE//CO.
E.g.4
Find ∠EDC, ∠DFE and ∠ECD.
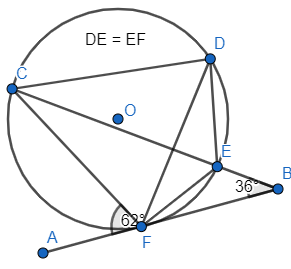
∠CFB = 180 - 62 = 1180 (angles on a straight line)
∠FCB = 180 - (36 + 118) = 260 (angles of a triangle)
∠FDE = ∠FCB (angles subtended by the same chord in the same segment)
∠FDC = 620 (alternate segment theorem)
∠EDC = ∠FDC + ∠FDE = 62 + 26 = 880
∠DFE = ∠FDE = 260 (FED is an isosceles triangle)
E.g.5
Find ∠AOB.
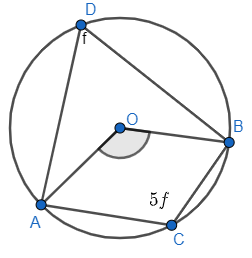
∠ADB + ∠ACB = 1800 (opposite angles of a cyclic quadrilateral)
5f + f = 180 => 6f = 1800
f = 300
∠AOB = 2 x ∠ADB (angles subtended by a chord at the centre is twice that of the same at the circumference)
∠AOB = 600
Challenge
Show that FEGH is a cyclic quadrilateral.