The Route Inspection Algorithm - Chinese Postman Problem
In this tutorial, you will learn the following:
- Eulerian Trail
- Semi-Eulerian Trail
- Traversable Graphs
- The Route Inspection Algorithm - Chinese Postman Problem.
- The Konigsberg Bridge Problem
- Travelling Salesman Problem - TSP
- Uses of Graph Theory
Eulerian Graphs and Semi-Eulerian Graphs
A graph is said to be Eulerian, if all the vertices are even. If it has got two odd vertices, then it is called, semi-Eulerian.
In the following image, the valency or order of each vertex - the number of edges incident on it - is written inside each circle.
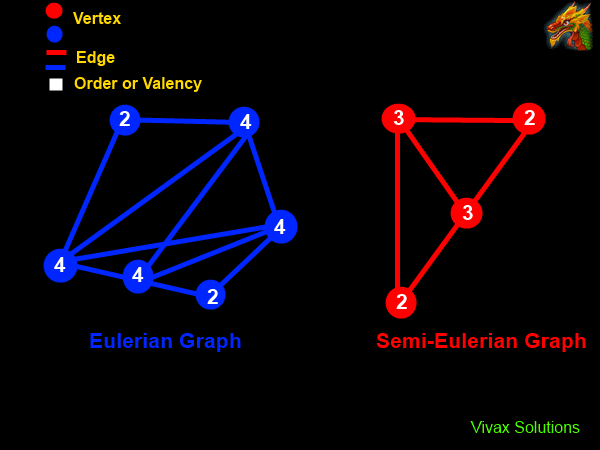
In the first image, all vertices are even; in the second, image there is a pair of odd vertices - with valency 3.
Traversable Graphs
A Graph is said to be traversable if it can be drawn without taking the pen off the paper and without retracing along the same edge, while returning to the starting point.
The following animation shows a traversable and a non-traversable graph: in the first, the turtle reaches the starting point without retracing along the same edge; in the second, on the other hand, the turtle retraces along the same edge while returning to the starting point.
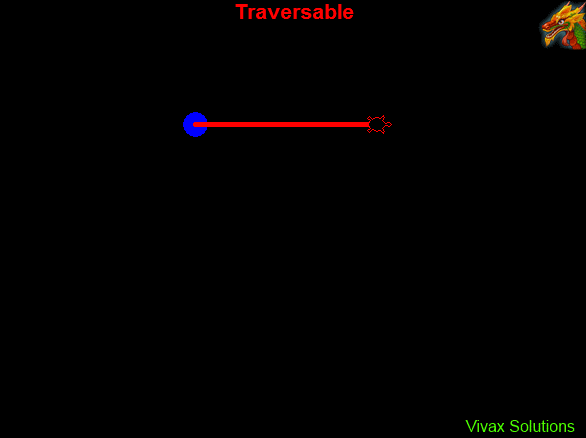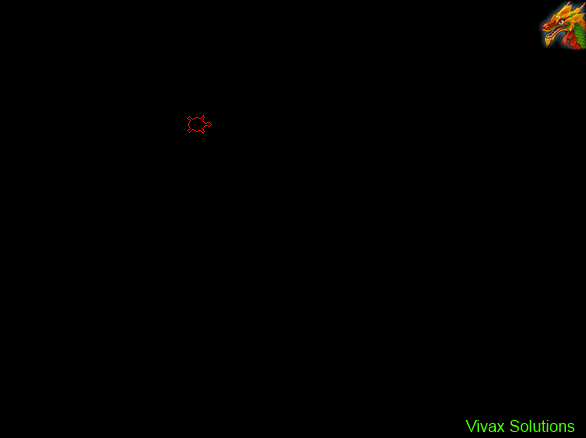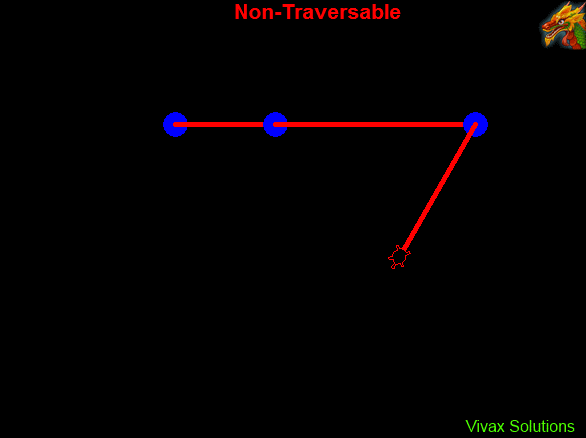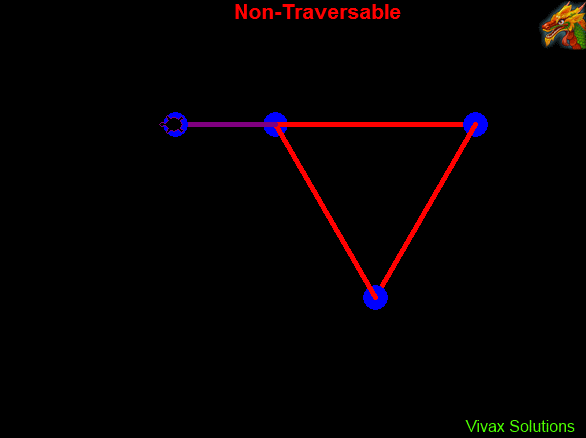
In the traversable graph, each vertex has an even number of degree or valency - 2, 2, 2. In the non-traversable graph, there the valency is a mixture of even numbers and an odd number - 2, 2, 2, 1.
Traversable Graph - Eulerian Trail
In the following animation, the the trail is traced without lifting the pen up, while moving along every edge. So, the Eulerian Trail is traversable.

As you can see, the graph is traversable regardless of the starting vertex; all vertices are even - with even valency.
Traversable Graph - Semi-Eulerian Trail
In the following animation too, the the trail is traced without lifting the pen up, moving along every edge. So, the Semi-Eulerian Trail is traversable. However, the start and end points must be the odd vertices - with odd valency.

In this case, however, the start and end points are the two odd vertices.
Making a Graph of Odd Vertices Traversable - pairing
As the above animations show, the presence of odd vertices in a graph is a hindrance to it becoming traversable. The presence of just two odd vertices - semi Eulerian case, for instance, makes the graph traversable only if the start and end vertices are of odd valency. If a graph has more than two odd vertices, it is not traversable. So, the only way to deal with the challenge is to make the vertices even. This is called pairing of odd vertices.
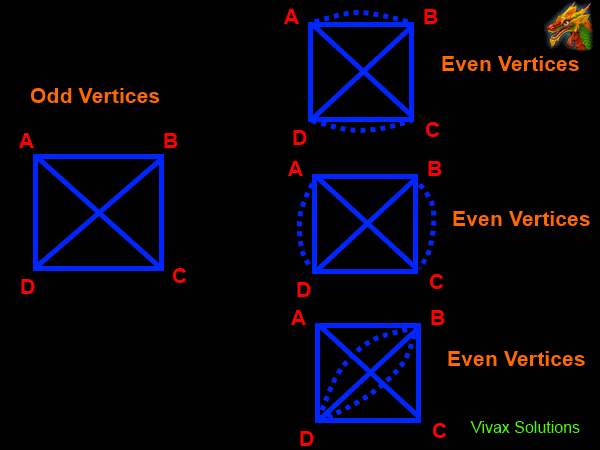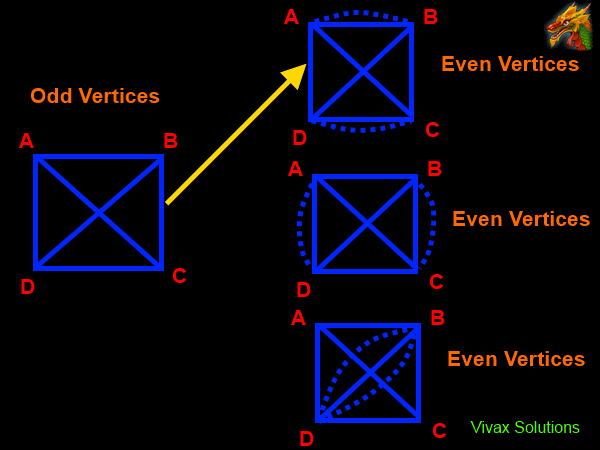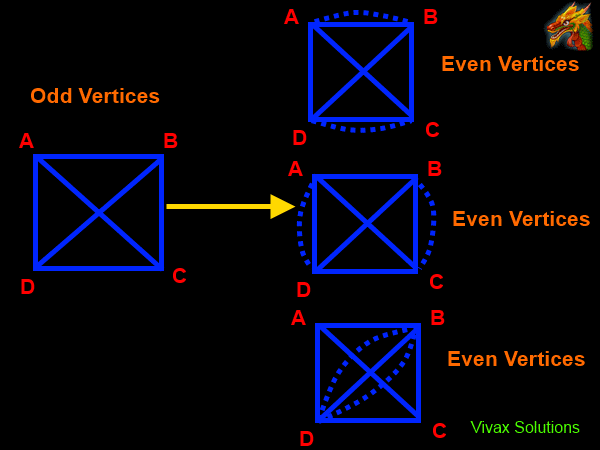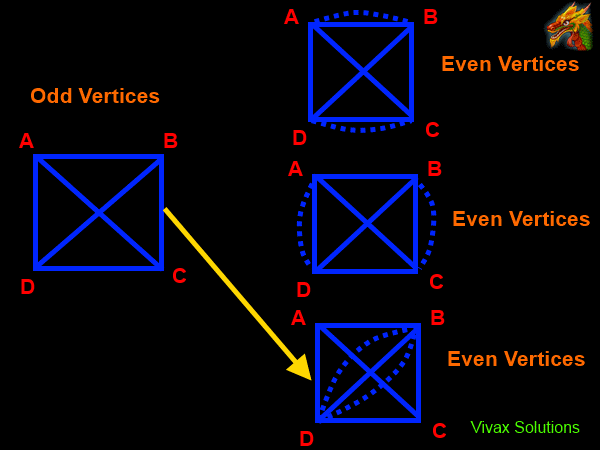
In the above example, there are four odd vertices. So, they can be paired up in three different ways to make the graph traversable; the greater the number of odd vertices, the greater the number of combinations of pairing up.
Euler's Hand Shaking Lemma
There must be an even number of odd vertices in every graph.
Proof:
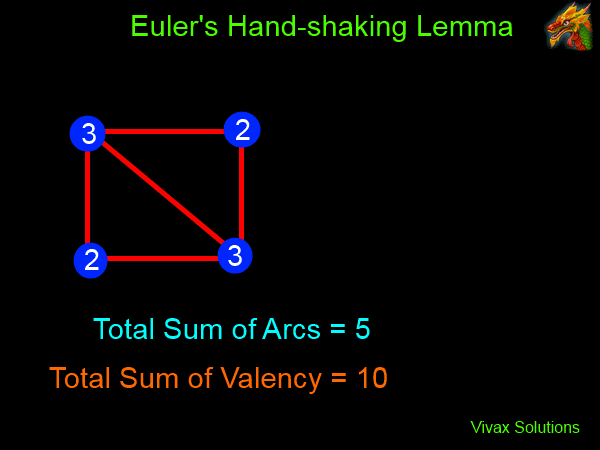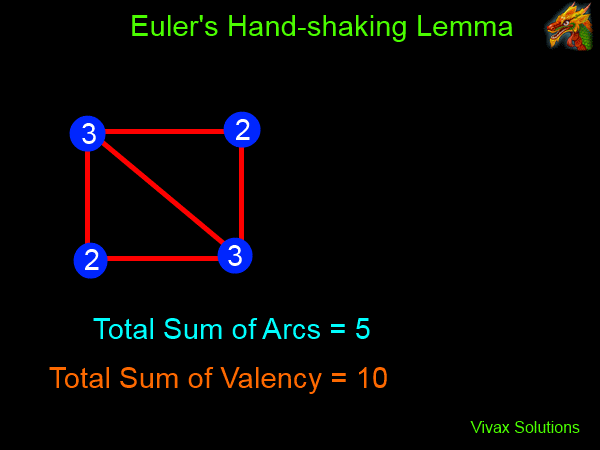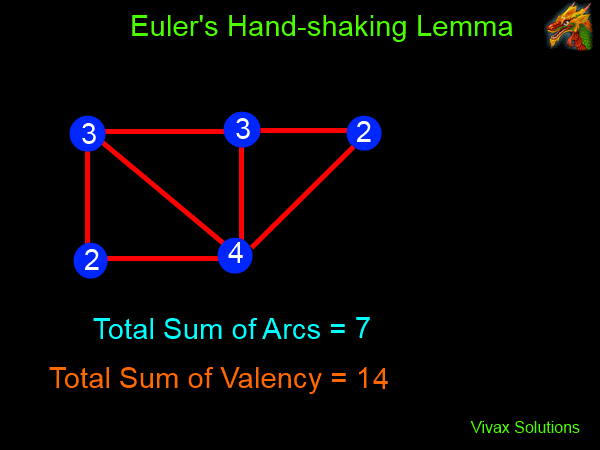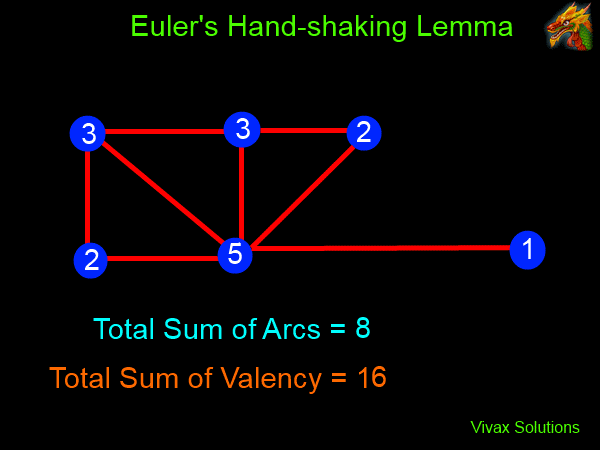
The animation shows that the addition of every arc to the graph increases the sum of valency by 2. As a result, the sum of valency always remains even. Therefore, any odd number must occur in pairs. Hence, the number of odd vertices must be even - or appear in pairs.
Formula for the Number of Pairings Possible
The following formula calculates the number of possible pairings for a graph of odd vertices:
N = n! / [2n/2 (n/2)!]; N= Possible Pairings; n = No of Odd Vertices
By using the following calculator, you can get the number of pairings once you enter the number of odd vertices of the network. Since odd vertices occur in pairs, an even number must be used in the calculator.
No of Odd Vertices:
You can see how the number of pairings exponentially goes up, as the number of odd vertices goes up.
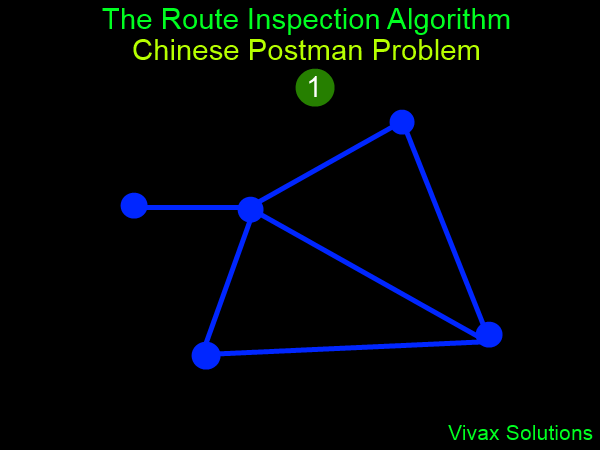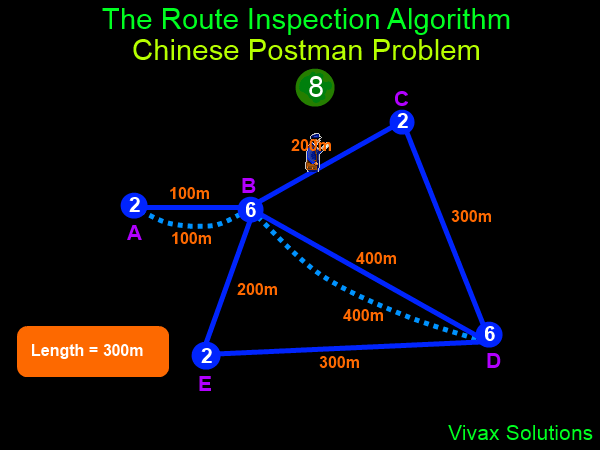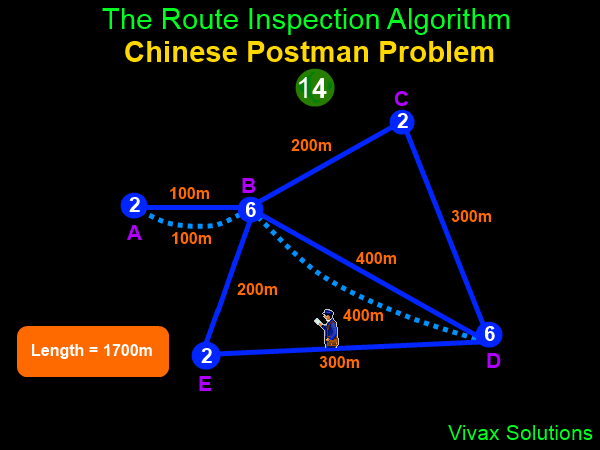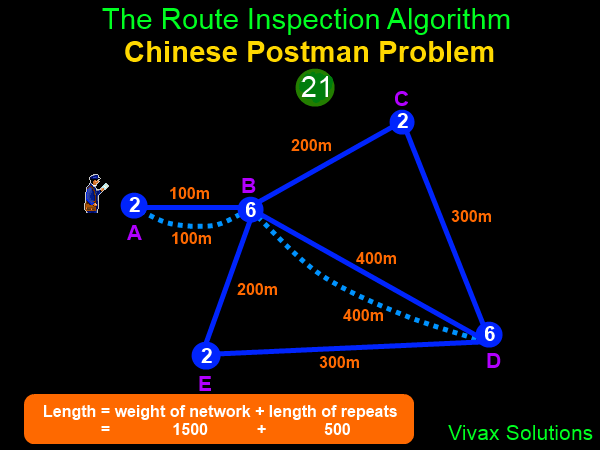
Route Inspection Algorithm - Chinese Postman Problem
In 1962, Kuan Mei-Koa, a Chinese mathematician, came up with what later became known as Chinese Postman Problem. He was
interested in a local postman, delivering mail to a number of streets in his locality in
such a way that the total distance walked by the postman could be kept to a minimum - starting and finishing at the same place, perhaps, the post office.
The algorithm is as follows:
- If all vertices are even, the total weight of the graph is the shortest distance.
- If there are only two odd vertices, pair up the arc/s between them, and then find the total weight of the graph.
- If there are more than two odd vertices, pair up all of them and then find the minimum added weight.
The following animation shows it:
The Travelling Salesman Problem - interactive
The Travelling Salesman Problem deals with the following:
You are given a list of cities and the distance between each pair of cities. The challenge is to find the shortest route go from one city and then back to it, after travelling through every one of them; the goal is to minimize the time taken for the journey and the cost.
With the following applet, you can practise it interactively. There are 9 cities - from A to I. Try moving the position of the points in green and see how the minimum distance changes. It's fun.
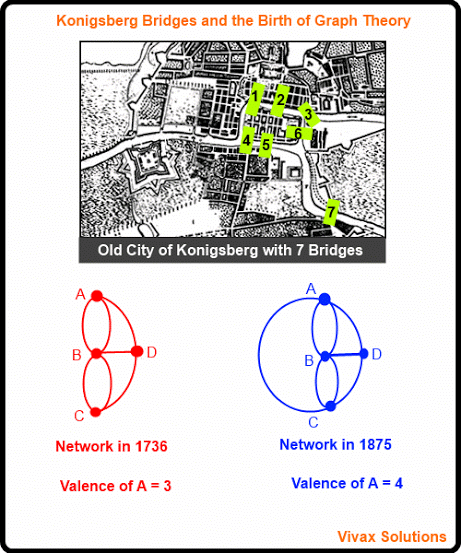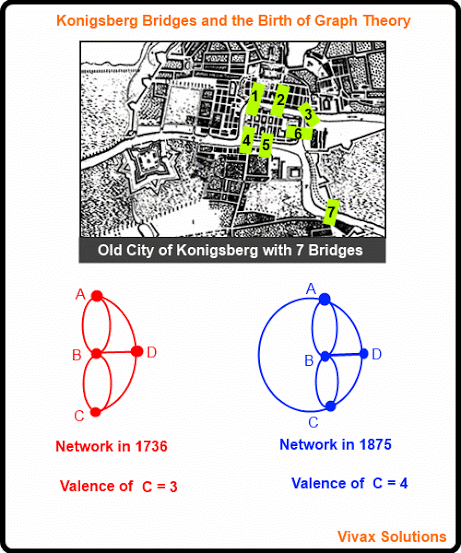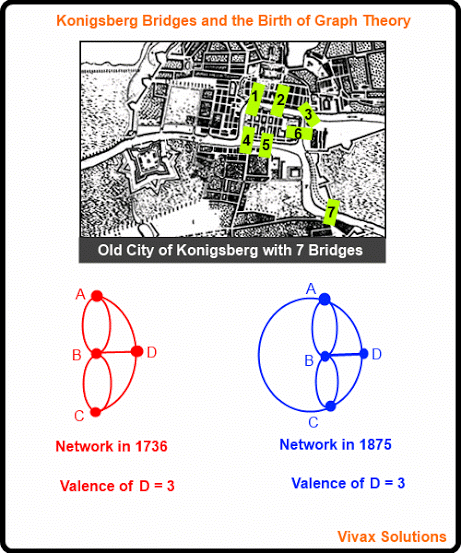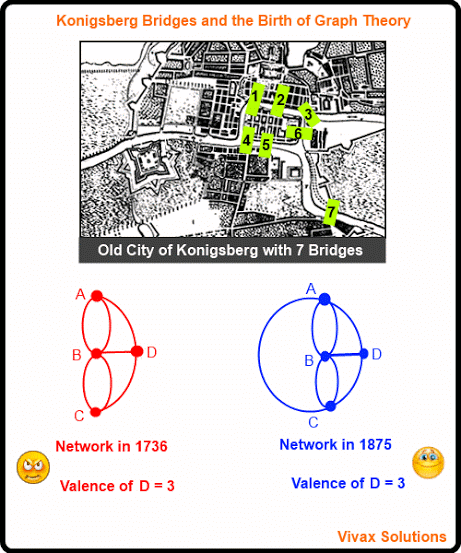
The Birth of Graph Theory - The Konigsberg Bridge
In the eighteenth century, there were seven bridges in connecting two islands in the city of Konigsberg, then part of Germany.
A debate had started in the city whether it would be possible to make a complete tour of the city, returning to the starting point, by crossing each bridge only once - crossing all of them, of course.
Since Leonhard Euler, the Swiss mathematician, happened to be in the city at that time, he got involved in the debate too. Having carefully studying the challenge, he declared that it was impossible: he said that one bridge has to be crossed at least twice to achieve the feat.
In order to solve the problem, Euler introduced a city plan called, a graph or network.
In his graph, the land areas were marked as vertices - A, B, C, D.
The bridges were drawn as lines between vertices, calling them edges or arcs.
So, Euler's network consisted of vertices and arcs.
Euler, then came up with the following formula to show why it is impossible to tour the city by crossing each bridge only once.
A path traversing the network by crossing every bridge just once is possible only if the network connected has at most two vertices with odd valence.
So, clearly the bridge network in the 18th century did not satisfy this rule, as all of them were of odd valency - travelling the city, by crossing each bridge only once was impossible.
In 1875, however, another bridge was added to the network by the authorities. Thanks to this addition, there were just two vertices, with a valency of an odd number in the network. In short, Euler's rule was satisfied.
The second network shows this arrangement. Euler showed that the second network of bridges can be crossed - each only once - in order to tour the whole city.
Uses of Graph Theory
- In mathematics, it is used to study and enhance the travelling time in complex flight paths, road networks leading to cities.
- In biology, it is used to study the migration patters of birds: the vertices and edges being habitats and potential migration paths respectively.
- Google uses Graph Theory to determine the significance of a web page, with the page being a vertex and hyperlinks connected to it being edges: the more links a page has, the more significant the page - and hence its rank - becomes; the higher the rank, the more likely it landing on the first page, in the event of a search being carried out.
- Even Facebook uses Graph Theory to evaluate the signficance of an individual, with the person and his friends linked to him being vertex and edges respectively.
If you want to expand your knowledge in the Graph Theory, here is a book for you: