Motion-Time Graphs

In this tutorial, you will learn the following:

Displacement and Distance

Distance is the amount of change in position of an object.

Displacement is the amount of change in position of an object in a certain direction.

Distance is a scalar and displacement is a vector. Displacement is equal to the shortest distance between two points in that direction.

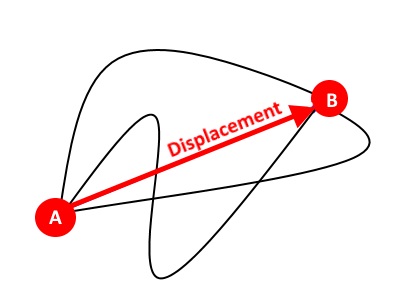
There are four paths between points A and B. The shortest path is the displacement between the two.

The following animation help you distinguish between displacement and distance.

Velocity

The rate of change of displacement - distance in a certain direction - is called the velocity.
Velocity = displacement /time
The gradient of a distance time graph is speed.
Units: ms^-1

 

 

Acceleration / Deceleration

The rate of change of velocity - speed in a certain direction - is called the acceleration or deceleration.
Acceleration = velocity / time
The gradient of a velocity time graph is acceleration or deceleration.
Units: ms^-2

The following animations show displacement / time graphs and their corresponding velocity / time graphs and acceleration / time graphs.

 

 

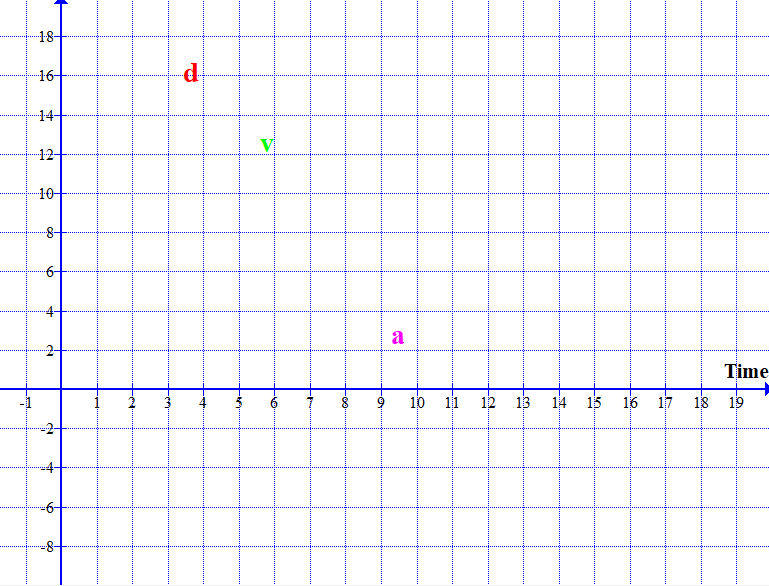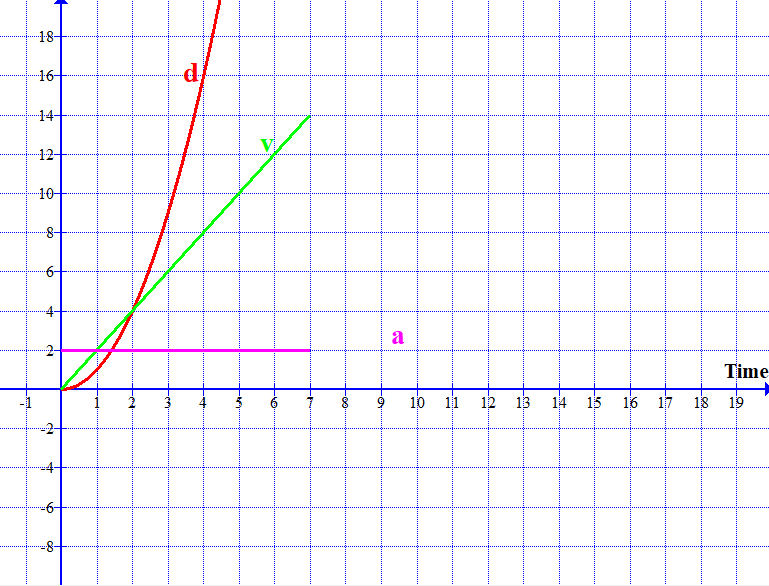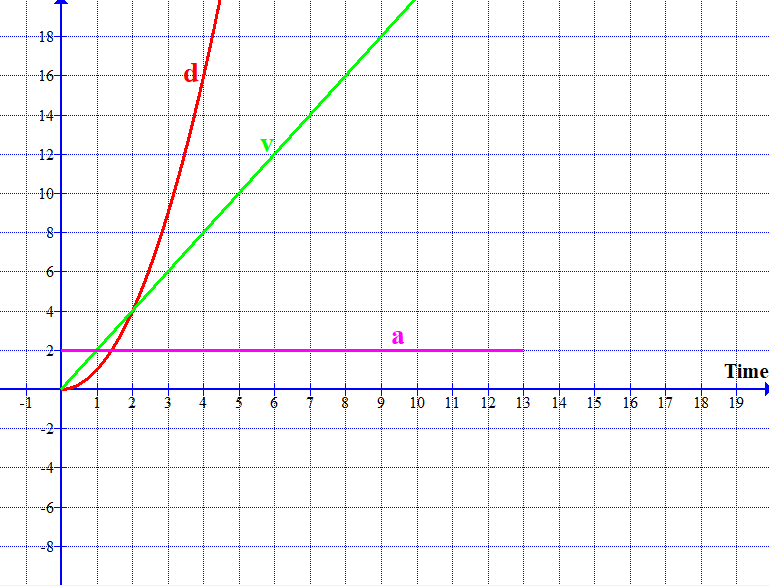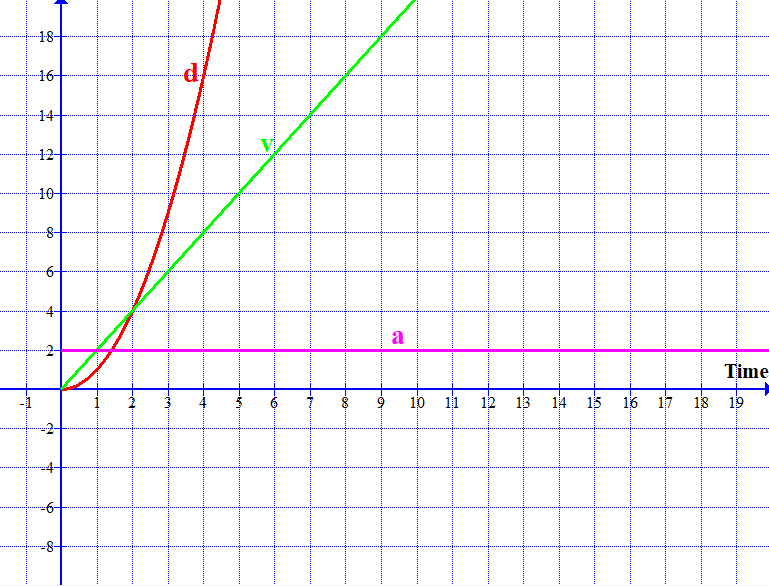
In the animations, please focus on the gradients of displacement-time graphs and velocity-time graphs, that will help understand the relationships.

Average Speed and Average Velocity

Average speed is defined as the total distance travelled by an object divided by the time taken for it.
Average Speed = Total Distance / Total Time

Average Velocity is defined as the total displacement travelled by an object divided by the time taken for it.
Average Velocity = Total Displacement / Total Time

E.g.1

The distance between Hounslow and Kingston is 9km. A man walks from Hounslow to Kingston at 4km/h, takes a rest at the latter for an hour and comes back at 6km/h. Find the average speed and velocity of the man.
Time taken for Hounslow to Kingston = 9/4 = 2.25 hrs
Time taken for Kingston to Hounslow = 9/6 = 1.5 hrs
Total distance = 18km
Total time= 2.25 + 1 + 1.5 = 4.75
Average speed = 18/4.75
= 3.8km/h
Total displacement = 0
Total time = 4.74
Average velocity = 0/4.75 = 0.

E.g.2

A cyclist travels one half of the distance to his destination at 10km/h and the other half at 15km/h. Find the average speed.

d, t₁, 10km/h

d, t₂, 15km/h

t₁ = d/10
t₂ = d/15
Total time = d/10 + d/15 = d[1/10 + 1/15] = d[25/150] = d/6
Total distance = 2d
Average speed = 2d/(d/6) = 12km/h.

E.g.3

A cyclist travels one half of the time taken to his destination at 20km/h and the other half at 30km/h. Find the average speed.

t, d₁, 20km/h

t, d₂, 30km/h

d₁ = 20t
d₂ = 30t
Total time = 2t
Total distance = 20t + 30t = 50t
Average speed = 50t/2t = 25km/h.

E.g.4

A, B and C are three towns. The distance between A and B is 60km and the distance between B and C is 90km. A man drives from B to C at 30km/h and then back to A at 15km/h. Find the average speed and velocity of the car.

A

B

C

Time taken for from B to C = 90/30 = 3hrs
Time taken for from C to A = 150/15 = 10hrs
Total time = 13 hrs
Total distance = 240km
Average speed = 240/13
= 18.5 km/h
Total displacement = -60km
Average velocity = -60/13 = 4.6
= 4.6km/h, towards A.

Equations of Motion

 

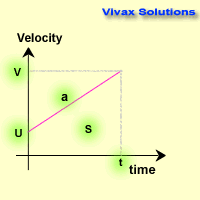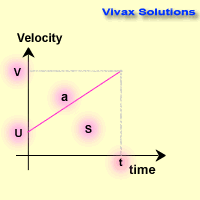
From the graph, a = v-u/t
v = u + at 1

From the graph, the area, s = ut + 1/2 (v-u)t
s = ut + 1/2 at² 2

From 1 => v² = u² + 2uat + a²t²
v² = u² + 2a(ut + 1/2 at²)
v² = u² + 2as 3

The Motion of a Ball Dropped from a Tower - interactive

Please use the buttons to drop the ball and reset.

The Motion of a Ball Thrown upwards...

The following animation models a ball thrown upwards until it comes back down and hits the ground.

 

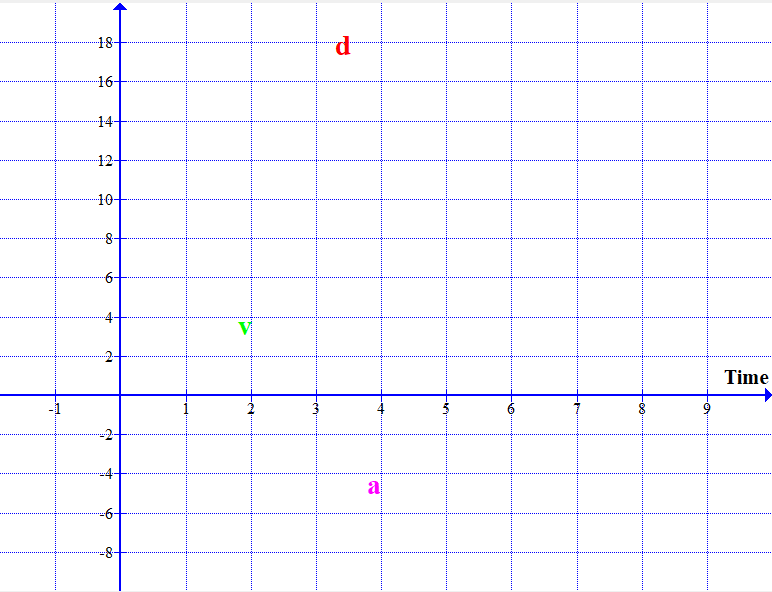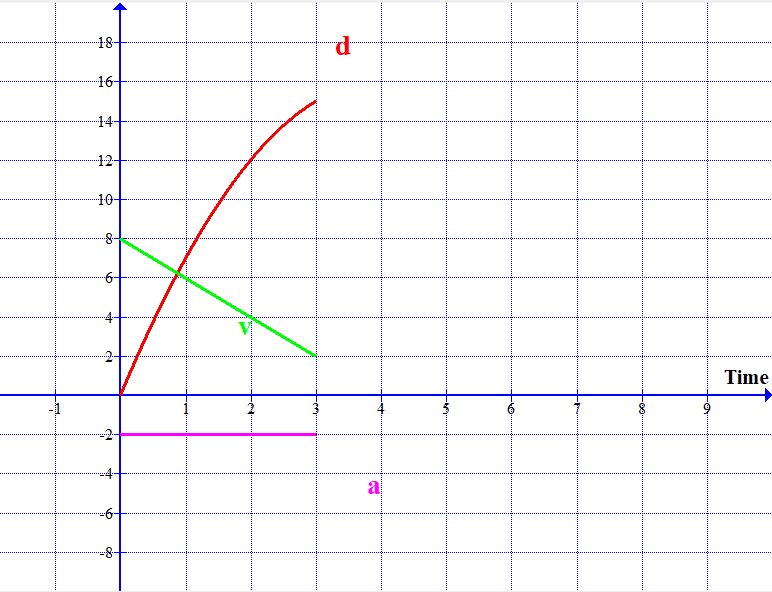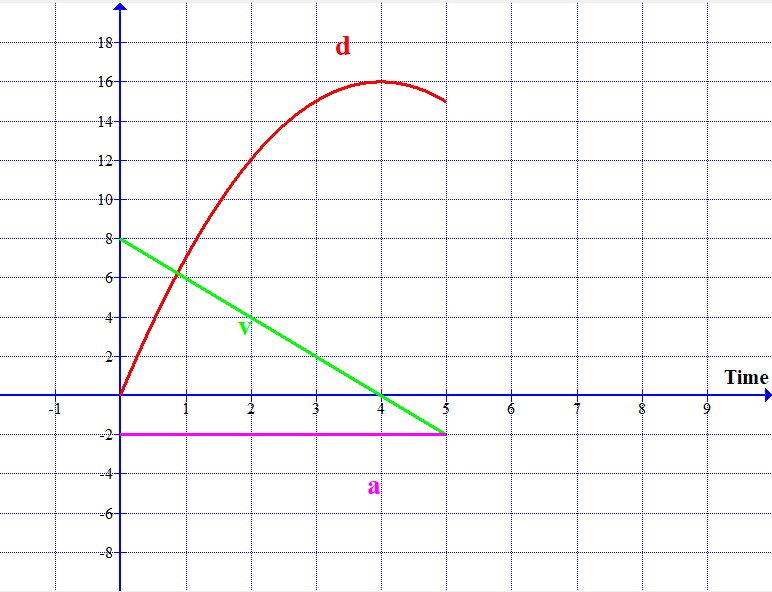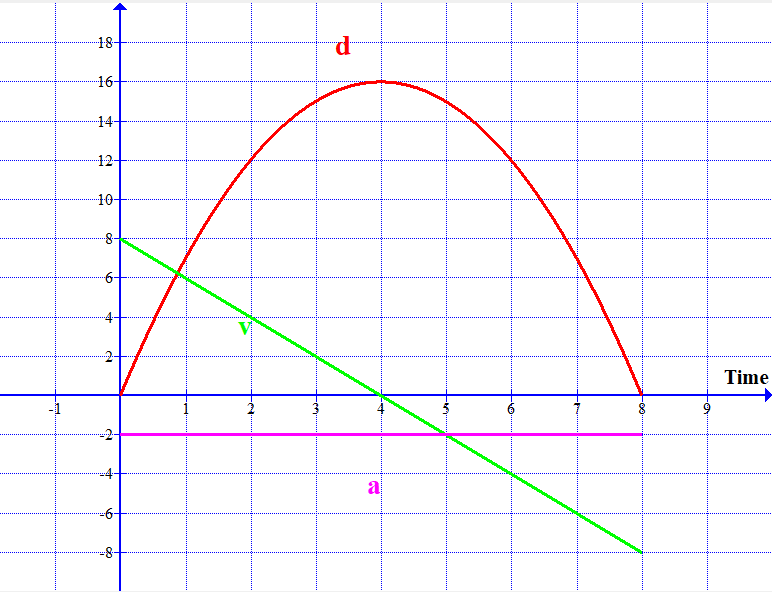
The velocity of the ball comes down, then becomes instantaneously zero and increases again. The corresponding dis;placement-time and acceleration-time graphs are shown on the same grid.

Instantaneous Velocity

If the displacement-time graphs is a straight line, the gradient at any point gives the velocity. If it is not a straight line, then, its gradient changes from point to point and so does the velocity of the object in question. In situations like this, we find the instantaneous speed by drawing a tangent at the point in order to find the gradient. The gradient gives the velocity at the point - instantaneous velocity.

With the following applet, you can practise it interactively. Move the slider - the time - and see the instantaneous velocity of the point of your choice.

E.g.

This problem is based on the above applet. You may check your answers with the above.

The displacement of an object against time is given by the formula, s = 4 - (t-2)². Find the following:

1. Find an expression for the instantaneous velocity at any time.
2. Hence, find the instantaneous velocity, when t = 1s, t = 3s and t = 5s.
3. Find the time, when the instantaneous velocity is zero.

1. s = 4 - (t-2)² = 4 - [t² - 4t + 4] = 4 - t² + 4t - 4 = 4t - t²
   v = ds/dt = 4 - 2t
   v = 4 - 2t
2. t = 1 => v = 4 - 2 = 2m/s
   t = 3 => v = 4 - 3 = -2m/s
   t = 5 => v = 4 - 10 = -6m/s
3. v = 4 - 2t
   v = 0 => 4 - 2t = 0
   t = 2s.

Problems for Practice

1. Draw distance-time graphs and corresponding velocity-time graph and acceleration-time graphs for the following:
   1. A ball dropped from the top of a tower
   2. A ball dropped from the top of a tower on to a perfectly elastic floor to be bounced back once
   3. A ball thrown upwards and then catch it again after a while
   4. The motion of an aircraft on landing after a long journey
   5. The motion of a parachutist when coming down
   6. The motion of a feather in the air
2. The distance between two towns is 240km. Two cars move at 60km/h and 40km/h towards each other at the same time. Find when and where they meet up.
3. Two trains remained stationary on the same railway track at a certain time, 60km apart. They moved towards each other at 40km/h and 20km/h respectively. At the same time, a bird started flying at 70km/h between the two trains up until they collided. How far would the bird have flown by the collision?
4. A car moves at a constant speed of 20km/h. At the same time, a motorcyclist starts moving from rest, and accelerates at 5ms^-2. Drawing velocity-time graphs on the same grid, find the following:
   1. The time taken by them to have the same speed
   2. The distance travelled by each
   3. When and where they meet up
5. A car starts from rest travels with an acceleration of 5ms^-2 for 4 hours. Then it slows down it velocity to 10km/h in the next two hours. During the last leg of the tour, the driver maintains the speed for 5 more hours. Draw a velocity time graph and find the total distance travelled. Hence, calculate the average speed for the journey.

 

Answers

Move the mouse over, just below this, to see the answers:

1. Drawing
2. 2.4hrs, 96km, 144km
3. 70km
4. 1. 4hrs
   2. 40km, 80km
   3. 8hrs, 160km
5. 120km, 10.9km/h