Parametric Equations

When the coordinates of curve are expressed in terms of a third independent variable - parameter - parametric equations are produced.

E.g.

y = 2t; x = t² - 3

Here, 't' is the parameter.

E.g.1

y = t² + 2; x = (t-3);
Now, we have a choice - finding the values of x and y manually by substituting the values of t or use algebra to find the Cartesian equation. Let's go for the latter.
t = (x+3) => y =(x + 3)² + 2
This can easily be sketched: basic quadratic curve translated -3 in the x-axis and 2 in the y axis.

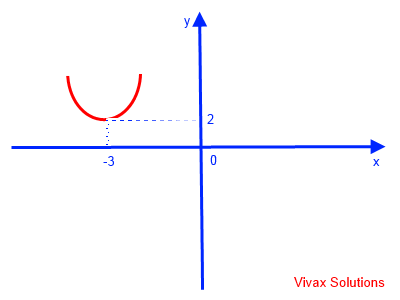
E.g.2

y = t; x = (t - 3)²;
t = √x+3 => y = √x + 3
This can easily be sketched as follows:

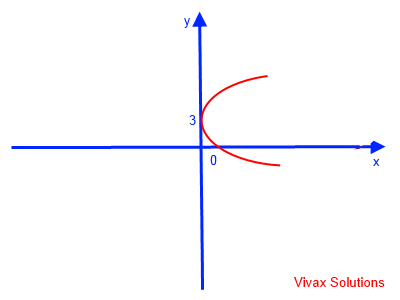
E.g.3

y = sec t; x = cos t
xy = cos t . 1/cos t
xy = 1
y = 1/x This is reciprocal curve.
This can easily be sketched as follows:

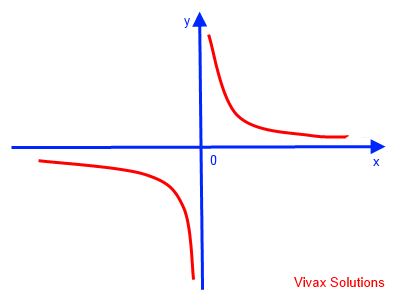
E.g.4

y = 3 sin t; x = 3 cos t
cos t = x/3; sin t = y/3;
x² / 9 + y² / 9 = sin² t + cos² t = 1
x² / 9 + y² / 9 = 1
x² + y² = 9
x² + y² = 3²
This is a circle with radius 3.
This can easily be sketched as follows:

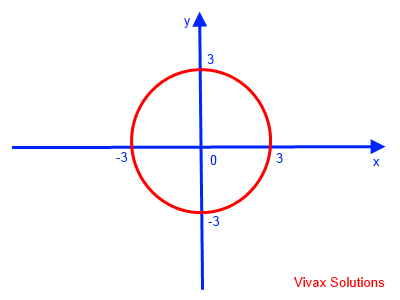
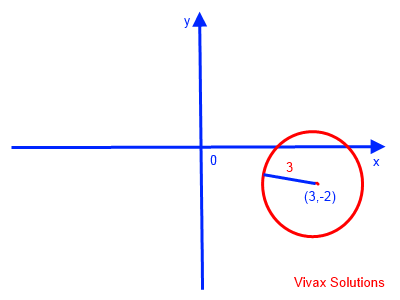
E.g.5

y = -2 + 3 sin t; x = 3 + 3 cos t
cos t = (x-3)/3; sin t = (y+2)/3;
(x-3)² / 9 + (y+2)² / 9 = sin² t + cos² t = 1
(x-3)² / 9 + (y+2)² / 9 = 1
(x-3)sup>2 + (y+2)² = 9
(x-3)² + (y+2)² = 3²
This is a circle with the centre at (3,-2) and radius 3.
This can easily be sketched as follows:

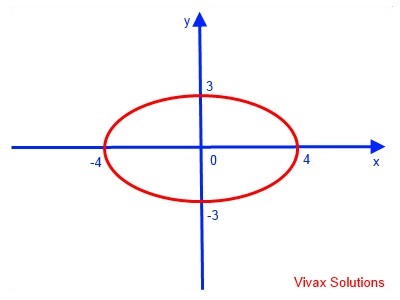
E.g.6

y = 3 sin t; x = 4 cos t
cos t = x/4; sin t = y)/3;
x²/16 + y² / 9 = sin² t + cos² t = 1
x² / 16 + y+² / 9 = 1
if x = 0 => y = +3 or -3
if y = 0 => x = +4 or -4
It is an ellipse. This can easily be sketched as follows:

The World of Spirals

The significance of parametric equations can be seen from the following beautiful shapes, which are produced by the manipulation of them in different ways.

Please press clear button, before choosing a new spiral, so that you can see each smoothly.

Parametric Equations - interactive practice

You can enter the parametric equations in terms of t in the two text boxes and then press the Enter key. After that move the slider to see the figure being built up on the Cartesian plane.

Area under a curve

Suppose we want to find the area under the curve, y = f(t), using parameter, t in the range, a<=x<=b. x = g(t).

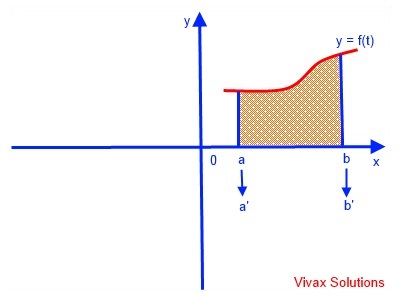
Area = _a∫^by dx
Since ∫ y dx = y (dx/dt) dt
Area = _a'∫^b'f(t) g'(t) dt
a' and b' are the boundaries in terms of t.

Area of a Circle

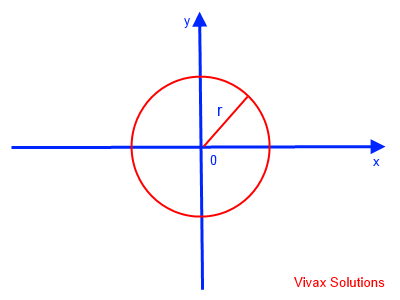
The parametric equations for the circle of radius r are as follows:
y = r sin (t); x = r cos(t); dx/dt = -r sin(t)
Area = ₀∫^2πy (dx/dt) dt
= ₀∫^2πr sin(t). -r sin (t) dt
= ₀∫^2π-r² sin²(t) dt
= ₀∫^2π-r² (1- cos(2t))/2 dt
= ₀∫^2π-r²/2 (1- cos(2t)) dt
= -r²/2 [t - sin(2t)/2]^2π₀
= -r²/2 [2π]
= -πr²

Area of a circle = πr²

Area of an Ellipse

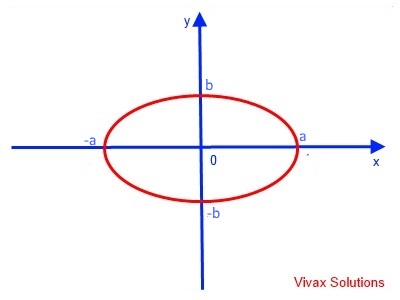
The parametric equations for the ellipse of semi-major axis and semi-minor axis a and b respectively are as follows:
y = a sin (t); x = b cos(t); dx/dt = -b sin(t)
Area = ₀∫^2πy (dx/dt) dt
= ₀∫^2πa sin(t). -b sin (t) dt
= ₀∫^2π-ab sin²(t) dt
= ₀∫^2π-ab (1- cos(2t))/2 dt
= ₀∫^2π-ab/2 (1- cos(2t)) dt
= -ab/2 [t - sin(2t)/2]^2π₀
= -ab/2 [2π]
= -πab

Area of an ellipse = πab

If a = b = r, it is a special case - a circle.
Area = πr²

Creating a Heart - interactive

In the following applet, two parametric equations involving trigonometry create a heart. The parameter changes from 0 radians to 2π radians. Please click the play button at the bottom.