Linear Interpolation
The following table shows the marks obtained for mathematics in a certain group:
| Class | Frequency |
|---|
| 11 - 20 | 10 |
| 21 - 30 | 18 |
| 31 - 40 | 30 |
| 41 - 50 | 10 |
| 51 - 60 | 14 |
| 61 - 70 | 16 |
| 71 - 80 | 2 |
Now, let's make the corresponding cumulative frequency table for the same data. It is as follows:
| Class | Frequency | Cumulative Frequency |
|---|
| 11 - 20 | 10 | 10 |
| 21 - 30 | 18 | 28 |
| 31 - 40 | 30 | 58 |
| 41 - 50 | 10 | 68 |
| 51 - 60 | 14 | 82 |
| 61 - 70 | 16 | 98 |
| 71 - 80 | 2 | 100 |
In order to plot a cumulative frequency graph, we have to plot cumulative frequency
against the upper-class-boundary of each class. The curve should look like the following:
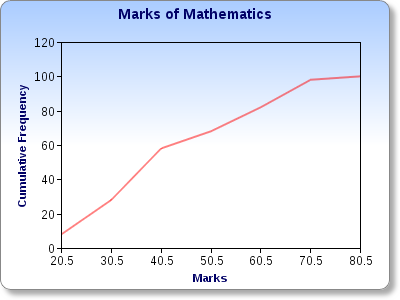
Finding the median
The median is the n/2 th value.
100/2 = 50
50th value.
50th value lies in the 31 - 40 class - i.e. anywhere between 30.5 and 40.5. We use linear interpolation to find it.
Since we treat the segment of the curve as a straight line in this class - shown in brown colour - the process is called linear interpolation. Let's consider the gradient of the line segment as follows:
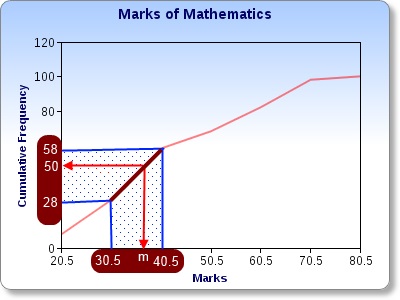
Gradient = (58-28)/(40.5-30.5)
Gradient = (50-28)/(m-30.5)
So, 30/10 = 22/(m-30.5)
3 = 22/(m-30.5)
3m - 91.5 = 22
3m = 113.5
m = 37.8
median = 37.8
Finding the first quartile - Q1
The first quartile is the n/4 th value.
100/4 = 25
25th value.
25th value lies in the 21 - 30 class - i.e. anywhere between 20.5 and 30.5. We use linear interpolation to find it.
Let's consider the gradient of the red line segment as follows:
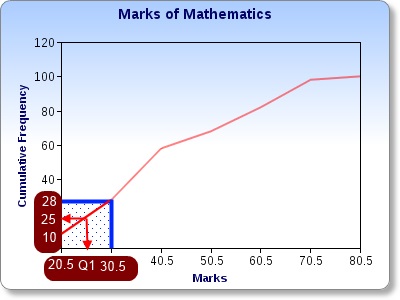
Gradient = (28-10)/(30.5-20.5)
Gradient = (25-10)/(Q1-20.5)
So, 18/10 = 15/(Q1-20.5)
1.8 = 15/(Q1-20.5)
1.8Q1 - 36.9 = 15
1.8Q1 = 51.9
Q1 = 28.8
First Quartile = 28.8
Finding the third quartile - Q3
The third quartile is the 3n/4 th value.
100 X (3/4) = 75
75th value.
75th value lies in the 51 - 60 class - i.e. anywhere between 50.5 and 60.5. We use linear interpolation to find it.
Let's consider the gradient of the yellow line segment as follows:
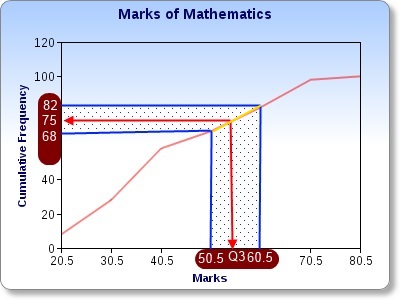
Gradient = (82-68)/(60.5-50.5)
Gradient = (75-68)/(Q3-50.5)
So, 14/10 = 7/(Q3-50.5)
1.4 = 7/(Q3-50.5)
1.4Q3 - 70.7 = 7
1.4Q3 = 77.7
Q3 = 55.5
Third Quartile = 55.5