Numerical Methods - Iteration for GCSE 9-1 and A-Level Pure Maths

In this tutorial, you will learn:

If f(x) is a function and it changes its sign from +ve to -ve or vice versa in a certain range of x, then a root of the function exists within the same range. The following image shows it:

 

 

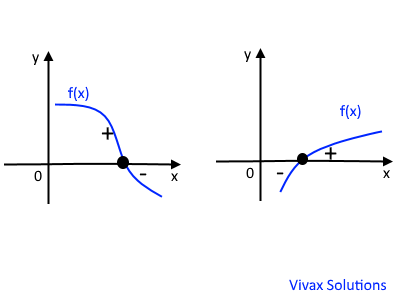
E.g.1Find a range of x in which a root for f(x) = x² -x -3 exists.

f(x) = x² -x -3
f(2) = 4 - 2 - 3 = -1 => -ve
f(3) = 9 - 2 - 3 = 4 => +ve
Since there is a change in sign in the range, 2≤ x ≤3, a root of the function exists in the same range.

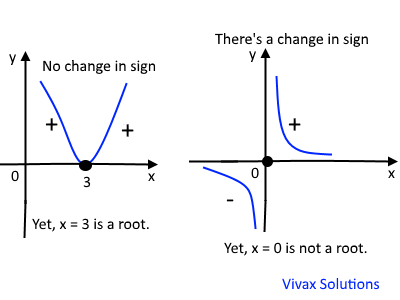
Exceptions

Sometimes, there is not a change in sign, yet there will be a root in a particular region. On the other hand, a change in sign does not necessarily indicate the existance of a root within a range. The following images illustrate this:

 

 

 

Iteration

If f(x) = 0 and it can be rearranged in such a way that x = g(x), where both f(x) and g(x) are functions of x, x = g(x) is said to be in iterative form.

E.g.

x² - x - 6 = 0

Let's make 'x' the subject of this equation; there are three possibilities:

• x = √(6 + x)
• x = x²- 6
• x = 1 + 6 / x

In the above iterations, g(x) = √(6 + x) or g(x) = x²- 6 or g(x) = 1 + 6 / x.

When the above equation - x² -x - 6 = 0 -  is written in one of the above forms with 'x' being the subject, they are said to be in an iterative form. That means, when the a value is substituted for 'x' on the right hand side the value of 'x' on the left can be obtained. Then the latter is put back in the equation to generate the other value. This goes on until, x approaches a constant value. This value is taken as a solution. Therefore, the actual iterative formula takes the following form, depending on the rearrangement.

• x_n+1 = √(6 + x_n)
• x_n+1 = x_n² - 6
• x_n+1 = 1 + 6/x_n

The first value of x - x₀ - is taken from a range of possibilities - guesses. Now let's solve one of the above equations using iteration.

x_n+1 = √(6 + x_n)

1. 
   First, guess a range where a solution could exist. Press the button and it will provide you with one.
2. 
   
3. 
   Now fill in the value of 'x₀' from one of the value you get and press the iterate button to find the solution:
   x₀ =
4. 
   
5. 
   

Have you noticed the way 'x' values approach the solution?; the longer you go the better.You can now see the beauty of iteration; it helps us find the root of an a function; since we have different forms of iteration, we can use some of them to find all the roots.

Have you noticed the way 'x' values approach the solution? The longer you go the better. You can now see the beauty of iteration; it helps us to find the solution of an equation; since we have different forms of iteration, we can use each one of them to find some of the roots, if not all.

E.g.1

Let's look at another simple example - a quadratic function.
x² - 10x + 5 = 0
x² = 10x - 5
:- x => x = 10 -5/x
x_n+1 = 10 -5/x_n
You can practise this interactively with the following applet: chose x₀ as 7, 8, 9 and 10 and see how it works; you will be amazed at the power and beauty of iteration.

 

 

Of course, in this simple example, a quadratic function was used for illustration. Iteration is generally used for higher polynomials such as cubic functions and more complex functions.

E.g.2

Find a root of the function, x³ + 4x - 3 by iteration.

f(x) = x³ + 4x - 3
f(0) = -3; f(1) = 2 => There is a change in sign between x = 0 and x = 1; therefore, a root could exist in the range.
Now, let's make the iterative formula.
x³ + 4x - 3 = 0
x = (3 - x³)/4
x_n+1 = (3 - x_n³)/4
Let x₀, the initial value = 0.
x₁ = 0.5
x₂ = 0.71875
x₃ = 0.65717
x₄ = 0.67904
x₅ = 0.67172
x₆ = 0.67422
x₇ = 0.673377...

So, the root is approximately, x = 0.673 (3 d.p.).

 

 

Iteration with Microsoft Excel

The following animation shows how to use Microsoft Excel in finding a root of a function by iteration.

E.g.

Find a root of the function, f(x) = x³ + 3x - 5 by iteration.

x_n+1 = (5 - x_n³)/3

f(1) = -1 => -ve; f(2) = 9 => +ve;
So, there must be a root between x = 1 and x = 2. The iteration will find it.
Let x₀ = 1.

 

 

As you can see, x = 1.67 is a root to 2 d.p.

Iteration - interactive practice with Python

You can experiment with iteration here: change the value of x in x and the number of iterationsn and experiment with it.

E.g.

Solve x² - x - 3 = 0.
x² - x - 3 = 0.
x² = x + 3
x = 1 + 3/x
x_n+1 = 1 + 3/x_n
You may use x₀ = 2 or 4 for the practice.

 

Finding the Square Root of a Number - interactive practice

Iteration can be used to find the square root of number. This is how it works:
Let x² = N
:-x => x = N/x
+x => 2x = N/x + x
:-2 => x = N/2x + x/2
x = 1/2[N/x + x]
x_n+1 = 1/2[N/x_n + x_n]
Take x₀ = 1 and iterate.