Unveiling the Binomial Distribution
Introduction:
Welcome to your interactive guide to the Binomial Distribution! Whether you're an A-Level student in the UK or a high schooler anywhere in the world, this tutorial is designed to make you a master of this fundamental probability concept.
Have you ever wondered about the chance of flipping heads three times in a row? Or maybe you're curious about the probability of getting exactly two perfect scores in a class of 20 students? These are classic examples of scenarios tackled by the Binomial Distribution.
In simpler terms, the Binomial Distribution helps us understand the likelihood of getting a specific number of successes in a series of independent trials, where each trial has only two possible outcomes (often called success and failure).
This interactive tutorial will break down the Binomial Distribution into manageable steps. We'll explore key concepts like calculating probabilities, using formulas, and interpreting results through engaging simulations and real-world examples.
By the end of this journey, you'll be able to confidently apply the Binomial Distribution to solve problems in your exams and beyond! So, buckle up and get ready to unlock the secrets of this powerful statistical tool.
Suppose that you have a coin that is biased with the probability of getting a Head being 2/3. Let's toss this coin three times and find the probability of getting two heads. Since these are independent events, the temptation is to calculate it in the following way:
P(two heads) = (2/3)(2/3)(1/3) = 4/27 1
sequence of HHT. However, there is no guarantee that it will happen in that order and we make a mistake in our calculation. There are more than one way to get two heads from three tosses. They are as follows:
HHT, HTH, THH
The probabilities are as follows:
P(HHT) = (2/3)2(1/3); P(HTH) = (2/3)2(1/3); P(THH) = (2/3)2(1/3);
Since these three events are mutually exclusive, the total probability is the sum of probabilities.
P(two heads) = 3(2/3)(2/3)(1/3) = 12/27 = 4/9 2
As you can see from the above calculations, that the answer in equation 2 is 3 times that of equation 1.
The number 3 comes from 3C2 - 3C2
(2/3)2 is the square of the probability of success - p2
(1/3) the probability of failure - (1-p)
Therefore, the probability of 2 heads from 3 tosses is given by the following formula:
P(two heads from three tosses) = 3C2(2/3)2(1/3)
In the same way, we can give a general formula for the probability of r successes in n trials, if the probability of success is p, in the following way. It is called the Binomial Distribution
X ~ B(n,p); P( X = r ) = nCr pr (1-p)n-r
Is Binomial Distribution, a true distribution ?
Let's say the values of success - r - are 0, 1, 2, 3, 4, ...........n
So, the corresponding probabilities - nCr pr (1-p)n-r - are nC0p0(1-p)n, nC1p1(1-p)n-1, nC2p2(1-p)n-2,
etc. The following table summarizes the distribution:
| t | P(X = r) |
| 0 | nC0p0(1-p)n |
| 1 | nC1p1(1-p)n-1 |
| 2 | nC2p2(1-p)n-2 |
| 3 | nC3p3(1-p)n-3 |
| -- | ------------ |
| n | nCnpn(1-p)0 |
So, Σ (P X = r) = Σ nCr pr (1-p)n-r =[p + (1-p)]n = 1 ---- from binomial expansion
Since the sum of probabilities adds up to 1, this is a true probability distribution.
Check list for Binomial Distribution
- There must be only two possible outcomes - success or failure
If there are more, they must be grouped as success or failure. For instance, when a die is rolled, there are 6 outcomes; so, to model by Binomial Distribution, you can group them as prime / no prime,
multiple of six / not multiple of six, odd / even etc.
- The probability of either success or failure must remain the same throughout trials
- The number of trials have a fixed limit
- The trials must be independent of each other.
Situations where Binomial Distribution model does not work:
- Rolling a die until a prime number is obtained - this can go on for ever
- Tossing a fragile coin for a large number of times - the coin will not remain unbiased due to wear and tear and probability of success or failure changes
Simulation of Binomial Distribution
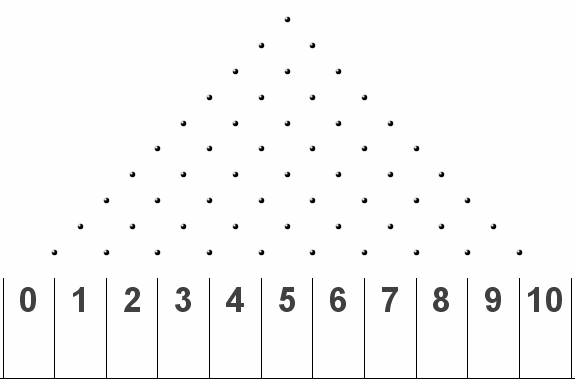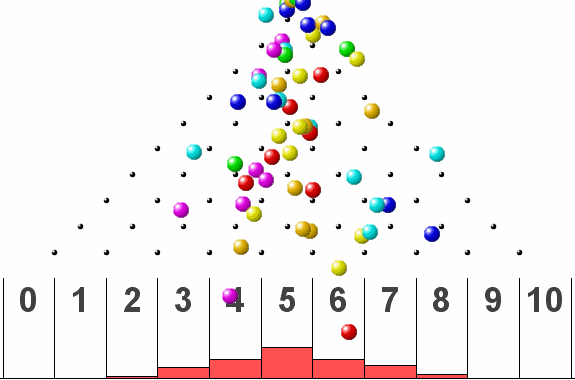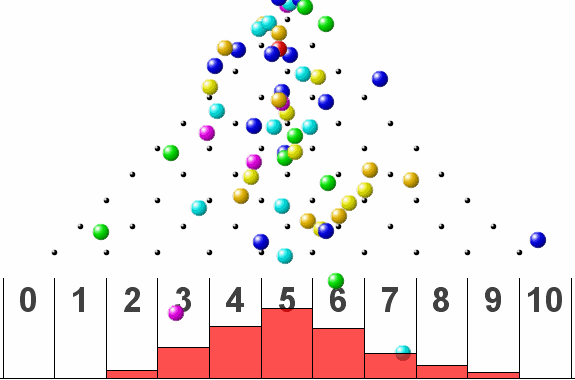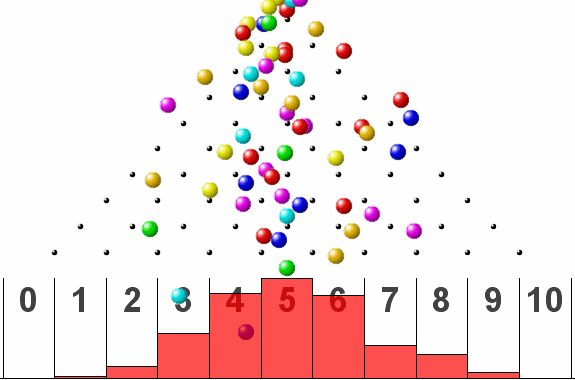
The above simulation uses a ball that comes down vertically through a grid of pins.
If the ball is deflected right on impact with a pin, it is considered as a *success.* If the deflection is to the left, it is considered as a *failure.*
In short, the probability of success or failure is 0.5. The distribution takes the typical symmetrical shape as the number of ball count increases.
You can use the following calculator in the calculations of Binomial Distribution.
Binomial Distribution Calculator
E.g.1
An unbiased coin is tossed 10 times. Find the following probabilities.
- Getting no Heads
- Getting two Heads
- Getting fewer than or equal 2 Heads
- Getting more than 3 Heads
- P(r = 0) = 10C0 (0.5)0 (0.5)10 = 0.001
- P(r = 2) = 10C2 (0.5)2 (0.5)8 = 0.0439
- P(r < = 2) = 10C0 (0.5)0 (0.5)10 + 10C1 (0.5)1 (0.5)9 + 10C2 (0.5)2 (0.5)8 = 0.001 + 0.0098 + 0.439 = 0.0538
- P(r > 3) = 1- P(r < = 2) = 1- 0.0538 = 0.9462
E.g.2
A fair die is rolled 8 times. The number of multiples of 3 obtained is noted. Find the following probabilities.
- Getting exactly 2 multiples of 3
- Getting fewer than 2 of multiples of 3
- Getting 3 or more than multiples of 3
- Getting no multiples of 3
- P(r = 2) = 8C2 (1/3)2 (2/3)6 = 0.2965
- P(r < 2) = 8C0 (1/3)0 (2/3)8 + 8C1 (1/3)1 (2/3)9 = 0.0576 + 0.1977 = 0.2553
- P(r > 3) = 1- P(r < = 2) = 1- 0.5518 = 0.4482
- P(r = 0) = 8C0 (1/3)0 (2/3)8 = 0.0576
E.g.3
Tina wants to get an A* in her physics examination at A Level. There are 20 multiple choice questions with 4 answers for each. She knows for sure that she got 12 questions right. She wants to get at least 16 of them right to reach her academic goal. What is the probability of Tina achieving her goal in the section of multiple choice questions of her physics paper?
Tina's physics test can be modeled by the Binomial Distribution.
Probability of success in this case = 1/4 = 0.25
X ~ B(20, 0.25)
Since she already got 12 questions right, she needs to get 4 or more right to get the required score.
P(X ≥ 4) = 1 - P(X ≤ 3) = 1 - 0.2252 = 0.7748
Probability of Tina achieving her goal = 0.7748
E.g.4
A weapon manufacturer claims that 92% of his cannon shells will work in a ceremonial firing. The army wants to perform a
21-gun-salute for a dignitary and has taken the possession of 25 of them, as a few spares will make sure an unexpected event will not happen. Calculate the probability of having enough cannon shells for the event?
As long as the number of cannon shells that potentially could misfire remains fewer than or equal to 4, the event will go ahead without a hitch.
Since the probability of the failure of a cannon shell = 1 - 92/100 = 0.08, the failure can be modeled by Binomial Distribution
X ~ B(25,0.08)
P(X ≤ 4) = 0.9877
Probability of the event happening without a hitch = 0.9877
E.g.5
The traffic lights at junctions in the United Kingdom operate in three phases: the red phase indicates that you need to stop; the amber phase that follows the red indicates 'getting ready to go' phase; when the green light comes, you are allowed to drive through them. Ben has to cross five traffic lights to get to work in the morning rush hour.The timing for the during of the three phases are 45%, 5% and 45% respectively. Ben is determined not to jump a traffic light and end up in the wrong book of the authorities; he waits until the green light comes on.
a) Can he model the set of events up until he manages to report to work by Binomial Distribution? Explain.
b) Find the probability that on a certain day that he has to stop at at least 3 stops.
a) Ben's traveling through the traffic lights can be modeled by Binomial Distribution - stopping at a traffic light or not.
b)Probability of stopping at a traffic light = 50% = 0.5
P(stopping) = 0.5
X ~ B(5, 0.5)
P(X ≥ 3) = 1 - P(X ≤ 2) = 1 - 0.5 = 0.5
You can practise the Binomial Distribution interactively here:
You can choose the number of trials(n), probability(p) and the range of values for which you need probabilities. Click the selector, [, [], or ], then movable slider will appear below the chart.
Please answer the following questions.
- If X ~ B(12,0.3), find the following:
- An unbiased coin is tossed 60 times. Find the following:
- Getting 15% of the tosses as Heads
- Getting between 20% to 30% of Tails
- A large stock of light bulbs are analyzed by a statistician, of which 5% are known to be faulty. If he picks up 5 bulbs at random, calculate the following probabilities.
- Getting no faulty bulb
- Getting fewer than 4 faulty bulbs
- Getting all faulty bulbs
- The probability of a certain cricketer hitting a six, in a limited over match, is 0.4. How many balls should he face before hitting seven sixes, with a probability of 0.85 ? How significant is the nature of the
- match being limited over in your calculations ?
- More and more Professional computer exams are conducted on screens in real time with multiple choice questions. Usually the there are 4 answers for each question. Find the probability of getting at least
6 of them right in a 20-questions exam.