Level 3 Mathematical Studies - Core Maths - Tutorial
In this tutorial, two major topics of the Finance section of Level 3 Mathematical Studies, also known as Core Maths, are fully covered. They are AER - the Annal Equivalent Rate - and APR - Annual Percentage Rate. The tutorial contains worked examples for both AER and APR that progress gradually so that the students can grasp the concepts clearly.
In addition, there is a calculator for calculating the monthly loan payments too, once the present value, interest rate and number of periods are entered.
AER - Annual Equivalent Rate
The interest rate for a savings account or an investment depending on the number of compounding periods in a year is defined as the Annual Equivalent Rate of the saving account or the corresponding investment. It is also known as the Annual Effective Rate.
Since the AER is different from the stated interest of an investment, the former calculates a more accurate value that the latter, especially thanks to the consideration of the compounding periods.
The AER is calculated by using the following formula:
r = (1 + i/n)n - 1, where i = nominal interest rate - the stated interest - in decimal form and n is the number of compounding period.the AER must be given as a percentage.
Nominal Interest Rate - i
This is calculated for a year in decimal form.
E.g.
If interest is 2% per annum, i = 2/100 = 0.02
If interest is 4% for six months, i = (2x4)/100 = 0.08
If interest is 3% for a quarter, i = (4x3)/100 = 0.12
If interest is 0.5% for six months, i = (2x0.5)/100 = 0.01
Number of Compounding Periods - n
E.g.
If interest is calculated annually, n = 1
If interest is calculated every six months, n = 2
If interest is calculates quarterly, n = 4
If interest is calculated monthly, n = 12
If interest is calculated weekly, n = 52
AER - Calculator
Food for Thought
Is the AER always greater than the quoted nominal interest rate? Explain.
E.g.5
The following table shows the savings options available from four banks. Calculate the worst and best return on investment - ROI. Hence calculate the best gain that an investment of £10,000 can offer, if invested for 8 years. Please calculate manually first and then check the above calculator to verify the answers.
| Bank |
Gross Interest Rate |
Compounding Period |
AER |
| Halefax |
5.3 |
Quarterly |
? |
| Barklays |
5.32 |
Daily |
? |
| Nazwest |
5.25 |
Monthly |
? |
| Sandtand |
5.28 |
Annually |
? |
Halefax:
i = (5.3)/100 = 0.053
n = 12/3 = 4
r = (1 + i/n)n - 1
r = (1 + 0.053/4)4 - 1 = 0.0541
AER = 5.41%
Barklays:
i = (5.32)/100 = 0.0532
n = 365
r = (1 + i/n)n - 1
r = (1 + 0.0532/365)365 - 1 = 0.0546
AER = 5.46%
Nazwest:
i = (5.25)/100 = 0.0525
n = 12
r = (1 + i/n)n - 1
r = (1 + 0.0525/12)12 - 1 = 0.0538
AER = 5.38%
Sandtand:
i = (5.28)/100 = 0.0528
n = 1
r = (1 + i/n)n - 1
r = (1 + 0.0528/1)1 - 1 = 0.0528
AER = 5.28%
The worst return of investment is from Sandtand, AER at 5.28% and the best is from Barklays - AER at 5.46% .
The value of the investment of £10,000, after 8 years = 10000(1 + 5.46/100)8 = £15300.37
The best gain = 15300.37 - 10000 = £5300.37
E.g.6
Paul Heron invests £12000 in January, 2024 in a bank that offers a gross interest rate, 5.2% per annum for 6 years in the hope that he will be able to buy a motorcycle that will cost around £13,500 with annual inflation. Will he have saved enough by then?
i = 5.2/100 = 0.052
r = (1 + i/n)n - 1
r = (1 + 0.052/1)1 - 1 = 0.052
r = 5.2%
The amount of money he has after 6 years = 10000(1 + 5.2/100)6 = £13554.84
Yes, he can save enough to buy the motorcycle of his choice.
E.g.7
Suppose you have a nominal interest rate of 6% per annum compounded quarterly. Calculate the Annual Equivalent Rate (AER) for this investment. Additionally, if the initial investment is £12,000, what will be the return after 2 years?
Given: Nominal interest rate (R) = 6% per annum, Compounding periods (n) = 4 (quarterly), Initial investment (P) = £12,000, Time (t) = 2 years
AER ≈ 6.136%
Return after 2 years: £13,466.56
E.g.8
If the nominal interest rate on a savings account is 8% per annum compounded monthly, what is the Annual Equivalent Rate (AER) for this account? Moreover, if the initial investment is £8,000, what will be the return after 3 years?
Given: Nominal interest rate (R) = 8% per annum, Compounding periods (n) = 12 (monthly), Initial investment (P) = £8,000, Time (t) = 3 years
AER ≈ 8.343%
Return after 3 years: £10,070.24
APR - Annual Percentage Rate
The Annual Percentage Rate (APR) is a standardized measure used to express the true cost of borrowing, including interest rates and additional fees, over a period of one year.
It provides borrowers with a comprehensive understanding of the total cost associated with a loan or credit product. APR allows consumers to compare different loan options effectively, enabling them to make informed financial decisions. For this course, additional fees are not taken into account while calculating the APR.
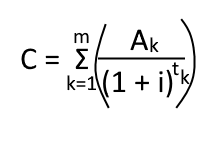
C = cost of loan | i = APR in decimal form | m = no of repayments | Akth = kth payment | tk = no of years elapsed between the start of the loan and the kth payment
Σ means adding each segment individually.
APR - Calculator
This calculator gives you the total loan amount, if you pay it in equal installments over a given period.
E.g.1
If a loan is taken in January, 2020 to be paid in 6 equal installments of £344.49 at APR, 12%, find the amount of the loan.
m = 6 | i = 0.12 | k: 1 - 6
C = 344.49/(1 + 0.12)1 + 344.49/(1 + 0.12)2 + 344.49/(1 + 0.12)3 + 344.49/(1 + 0.12)4 + 344.49/(1 + 0.12)5 + 344.49/(1 + 0.12)6 ≈ £1416.33
E.g.2
A loan is taken out that is to be paid in 3 equal installments of $250.75 at an APR of 8%. Find the amount of the loan.
m = 3 | i = 0.08 | k: 1 - 3
C = 250.75/(1 + 0.08)1 + 250.75/(1 + 0.08)2 + 250.75/(1 + 0.08)3 ≈ £646.21
E.g.3
Sam takes out a loan of £5000 at APR 12%. He plans to pay it back with two equal installments of £1500.00 and one more final payment. Calculate his final payment.
In this case, let the final payment, the third payment, be A3.
m = 3 | i = 0.12 | k: 1 - 3 | C = 5000
5000 = 2000/(1 + 0.12)1 + 2000/(1 + 0.12)2 + A3/(1 + 0.12)3
A3/(1 + 0.12)3 = 5000 -(2000/(1 + 0.12)1 + 2000/(1 + 0.12)2) = 1619.89
A3 = (1 + 0.12)3 x 1619.89 = 2275.82
Final payment = £2275.82
E.g.4
Sarah takes out a loan of £3000 at APR 8%. She plans to pay it back with two equal installments. Calculate her each payment.
In this case, let each payment be A.
m = 2 | i = 0.08 | k: 1 - 2 | C = 3000
3000 = A/(1 + 0.08)1 + A/(1 + 0.08)2
3000 = A(1/1.0811 + 1/1.0812)
A = 3000 / (1/1.0811 + 1/1.0812) = 1682.30
Each payment = £1682.30
Monthly Loan Payment Calculator - PMT
The calculator is equivalent to PMT function in Excel and Google Sheets with one notable exception - clarity for the user: you just have to type in the annual interest rate, APR, as a percentage and the period of payments as the number of years. It gives out the monthly payment, excluding the handling fee and other bureaucratic developments. Unlike spread-sheet based functions, it is user-friendly, as the what goes into the function such as the APR, number of periods and present value are clearly described for a potential user.
E.g.
Calculate the monthly payment for a loan, £50,000, taken at 5.5% APR to be paid in 20 years.
Pv = present value = 50,000 | APR = 5.5% | Number of Periods in Years = 20
If you plug them into the calculator, the monthly payment is given as £343.94.