Functions and Transformation of Graphs

Functions

y = x² + 3x -2 is said to be a function of x - an expression of x. This can also be written, in a bit more advanced way as f(x) = x² + 3x -2 - it is read as you write, function of x, f(x)
So, f(x) = x² + 3x -2
Now whatever you put in as 'x' on the left, substitutes 'x' on the right.

E.g.

• f(2) = 2² + 3x2 -2 = 4 + 6 - 2 = 8
• f(-2) = (-2)² + 3x(-2) -2 = 4 - 6 - 2 = -4
• f(0) = 0² + 3x0 -2 = 0 + 0 - 2 = -2
• f(x+1) = (x+1)² + 3(x+1) -2 = x² + 2x + 1 + 3x + 3 -2 = x² + 5x + 2
• f(x-1) = (x-1)² + 3(x-1) -2 = x² - 2x + 1 + 3x - 3 -2 = x² + x - 5
• f(2x) = (2x)² + 3(2x) -2 = (2x)² + 6x -2 = 4x² + 6x - 2
• f(x/2) = (x/2)² + 3(x/2) -2 = x²/4 + 3x/2 -2 = x²/4 + 3x/2 - 2

There are three major transformations:

1. Translation
2. Reflection
3. Stretching

Let's apply the above transformations to the following curve.

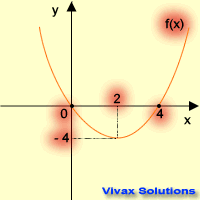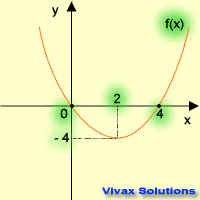
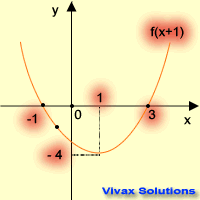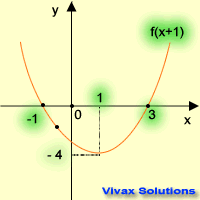
Translation

f(x) -----> f(x+1)	f(x) -----> f(x-1)
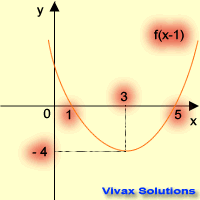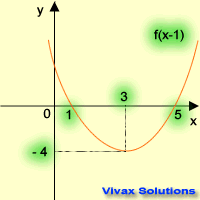translation in the -ve x-axis	translation in the +ve x-axis

f(x) -----> f(x) + 2	f(x) -----> f(x) - 2
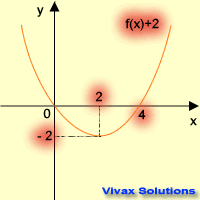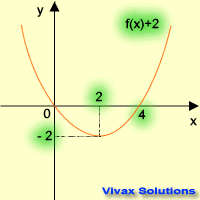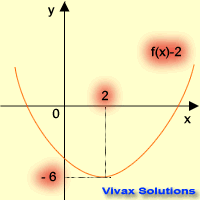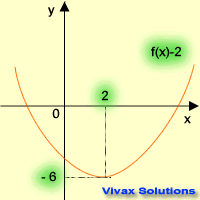translation in the +ve y-axis	translation in the -ve y-axis

You can animate the following curves to see how translation works. Please select an option and then move the sliders.
Choose slider, a, for the translation in the x-axis.
Choose slider, c, for the translation in the y-axis.

 

Reflection

f(x) -----> f(-x)	f(x) -----> -f(x)
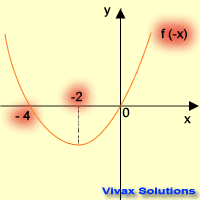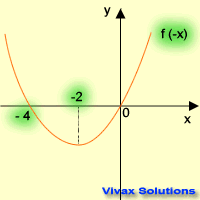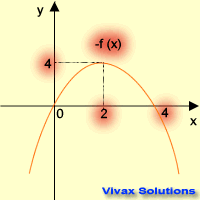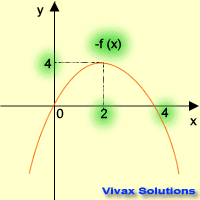reflection in the y-axis	reflection in the x-axis

Stretching

f(x) -----> f(2x)	f(x) -----> 2f(x)
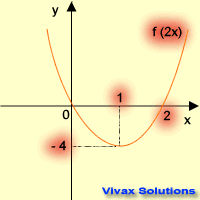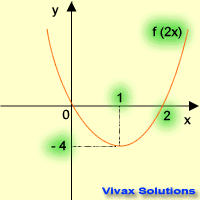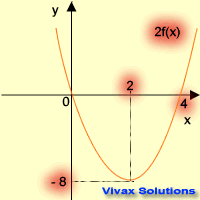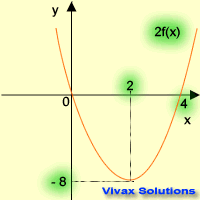stretching parallel to x-axis	stretching parallel to y-axis

You can animate the following curves to see how stretching works. Please select an option and then move the sliders.
Choose slider, a, for the stretching parallel to y-axis.
Choose slider, c, for the stretching parallel to x-axis.

 

Now, let's apply the transformation to some of the well-known curves.

E.g.1

Sketch f(x) = x² + 2x -3, and find the following:

• line of symmetry
• minimum value
• translations from f(x) = x²
• solutions

 

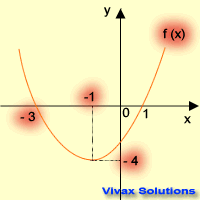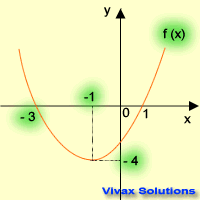
First of all, let's use the completing the square method:
Let x² + 2x -3 = (x+a)² +b
x² + 2x -3 = x² + 2ax + a²+ b
Make the coefficients of x², x and the constant on either side equal.
2a = 2 => a = 1
a²+ b = -3 => b = -4
f(x) = (x+1)² -4
Line of symmetry, x = 1
Minimum value = -4
This is a translation of f(x) = x², 1 in the negative x-axis and 4 in the negative y-axis.
The solutions are, x = -3 and x = 1

E.g.2

 

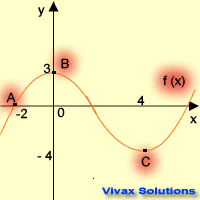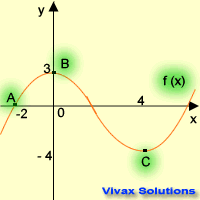
This question is based on the curve on the left; find the coordinates of A, B and C after the following transformations. The answers are on the table.

Transformation	New Coordinates
f(x+1)	A( -3 , 0 )	B( -1 , 3 )	C( 3 , -4 )
f(x-1) + 2	A( -1 , 2 )	B( 1 , 5 )	C( 5 , -2 )
f(2x)	A( -1 , 0 )	B( 0 , 3 )	C( 2 , -4 )
f(x/2)	A( -4 , 0 )	B( 0 , 3 )	C( 8 , -4 )
2f(x)	A( -2 , 0 )	B( 0 , 6 )	C( 4 , -8 )
f(-x) + 1	A( 2 , 1 )	B( 0 , 4 )	C( -4 , -3 )
-f(x) + 2	A( -2 , 2 )	B( 0 , -1 )	C( 4 , 6 )

Combination of Transformations

Here is an opportunity for you to practise transformations using a sine curve. The curve is in the form of y = a + b sin(cx + d). Change the values of a, b, c and d or to see the corresponding change. This is the best form of mastering the transformations.

 

Now, in order to complement what you have just learnt, work out the following questions:

1. Use the completing the square method to sketch f(x) = x² + 3x -4. Then describe the transformations of f(x) = x² to get this particular shape. Write down the minimum value and the line of symmetry too.
   • Show that the reflection in the y-axis of f(x) = x⁴ - 2x² + 5 is the same as f(x).
   • Write down a function that shows f(x) = -f(-x). Hence, sketch 2f(x) and f(2x) of the same function.
2. If f(x) = x² + 2x, sketch the following:
   • f(-x)
   • -f(x) + 2
   • f(x+2) - 3
   • f(2-x)
   • 2f(x) + 1
   • f(2x) - 3
3. Sketch f(x) = x² -x - 6 and hence sketch g(x) = (x+2)(x+3) and show that f(x+1) = g(x).
4. Sketch f(x) = 1 +2 sin(x) and solve f(x) = 1.3 for 0 < x < 360. What is the minimum value and maximum value of the function?<
5. Sketch f(x) = 1 + cos(3x) and hence find the period of the function, maximum value and minimum value.
6. Sketch f(x) = 3 - 2sin(3x) and hence find the period of the function, maximum value and minimum value.
7. Sketch f(x) = 1/x and then transform as follows:
   • f(-x) + 2
   • -f(x) + 2
   • 2f(x) - 3
8. The maximum value of f(x) = q + p cos(x) graph is 7 and the minimum is 1. find p and q.